Прямая be проведенная параллельно боковой стороне cd трапеции abcd отсекает треугольник abe 12

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4.^$$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям — подобны.

$$ 4.^$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4.^$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.^$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.^$$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4.^$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.^$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.^$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

$$ 4.^$$.В равнобокой трапеции `d^2=c^2+ab`, где `d` — диагональ, `c` — боковая сторона, `a` и `b` основания.

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4.^$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.^$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Докажем, например, утверждение $$ 4.^$$ .

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«||«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4.^$$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` — его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` — её точка пересечения с прямой `BC` (рис. 30б).

По построению `ACKD` — параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`

(т. к. угол `BDK` — это угол между диагоналями трапеции).

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Пусть `BC=a`, `AD=b`, и пусть `h` — высота трапеции (рис. 31). По свойству $$ 4.^$$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Трапеция равнобокая, по свойству $$ 4.^$$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4.^$$

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.^$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

$$ 4.^$$. Если `S_1` и `S_2` — площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.

$$ 4.^$$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` — какая-то сторона (или диагональ трапеции), `alpha` — смотрящий на неё вписанный угол.

Видео:Сложные примеры с поиском периметра 3 задание проф. ЕГЭ по математикеСкачать

Прямая, проведённая параллельно боковой стороне трапеции через конец меньшего о…

Прямая, проведённая параллельно боковой стороне трапеции через конец меньшего основания, равного $7$, отсекает треугольник, периметр которого равен $28$ (см. рис.). Найдите периметр трапеции.

Объект авторского права ООО «Легион»

Видео:ЕГЭ Математика Задание 6#27835Скачать

Вместе с этой задачей также решают:

Параллелограмм и прямоугольник имеют одинаковые стороны. Сколько градусов составляет острый угол параллелограмма, если его площадь относится к площади прямоугольника как $1:√ $?

Основания равнобедренной трапеции равны 20 и 50, а её боковые стороны равны 17. Найдите площадь трапеции.

В треугольнике $ABC$ угол $A$ равен $67^°$, а углы $B$ и $C$ — острые. $BD$ и $CE$ — высоты, пересекающиеся в точке $O$ (см. рис.). Найдите угол $DOE$. Ответ дайте в градусах.

Площадь параллелограмма равна 160, две его стороны равны 10 и 20. Найдите большую высоту этого параллелограмма.

Видео:Геометрия Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CDСкачать

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 13, отсекает треугольник, периметр которого равен 23?

Математика | 1 — 4 классы

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 13, отсекает треугольник, периметр которого равен 23.

Найдите периметр трапеции.

Будут вопросы — пиши) (P.

S. прости за почерк)).

Имеем трапецию АВСД, меньшее основание АВ = 13 см.

Проведя ВЕ параллельно АД, получили параллелограмм АВЕД (в котором стороныАД = ВЕ иДЕ = АВ = 13 см) и треугольник ВСЕ.

ПериметрΔ = ВС + СЕ + ВЕ = 23 см.

Видно по чертежу (т.

К. АД = ВЕ), что периметр трапеции больше периметраΔ на сумму длин (АВ + ДЕ) и равен23 + 2 * 13 = 49 см.

Периметртрапеции = АВ + ВС + СД + АД = АВ + ВС + (СЕ + ДЕ) + АД.

Подставим АВ = 13 = ДЕ и АД = ВЕ, получим, что периметр трапеции = 13 + ВС + СЕ + 13 + ВЕ = 26 + (ВС + СЕ + ВЕ) = 26 + 23 = 49 см.

Видео:Задание 3 ЕГЭ по математике. Урок 88Скачать

Основания равнобедренной трапеции равны 2 и 11, а периметр равен 28?

Основания равнобедренной трапеции равны 2 и 11, а периметр равен 28.

Найдите площадь трапеции.

Видео:35. Геометрия на ЕГЭ по математике. Трапеция.Скачать

Основание равнобедренного треугольника в 2 раза меньше чем боковая сторона а его периметр равен 20см?

Основание равнобедренного треугольника в 2 раза меньше чем боковая сторона а его периметр равен 20см.

Найдите боковую сторону.

Видео:Урок 2. №23 ОГЭ. О боковой стороне трапеции, если ее угол В=60 и С=135 градусов. Соотношения сторонСкачать

Основания равнобедренной трапеции равны 2 и 11, а периметр равен 28?

Основания равнобедренной трапеции равны 2 и 11, а периметр равен 28.

Найдите площадь трапеции.

Видео:Геометрия Через вершину C трапеции ABCD проведена прямая, которая параллельна боковой стороне ABСкачать

1. Найди основания трапеции, если одно из оснований на 6см короче другого?

1. Найди основания трапеции, если одно из оснований на 6см короче другого.

Боковые стороны равны 12см и 18см, а периметр трапеции равен 80см.

2. Вычислите площадь трапеции, если одно из оснований равно 84м, а второе составляет от первого 80% и высота равна 36м.

3 Найдите среднюю линию равностороннего треугольника, если его периметр равен 72 см.

Найдите среднюю линию трапеции, если площадь равна 9, 18 см2 и высота 27мм.

Видео:Задание 3 ЕГЭ по математике. Урок 41Скачать

Боковые стороны трапеции 13см и 15 см?

Боковые стороны трапеции 13см и 15 см.

Периметр равен 48см найдите среднюю линию трапеции.

Видео:🔴 В трапеции ABCD известно, что AB=CD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Трапеция поделена На равносторонние Треугольнике?

Трапеция поделена На равносторонние Треугольнике.

Чему равен периметр трапеции, если сторона равностороннего треугольника равна 8 см ?

Видео:Трапеция, решение задач. Вебинар | МатематикаСкачать

Основания равнобедренной трапеции равны 23 и 47, а ее периметр равен 96?

Основания равнобедренной трапеции равны 23 и 47, а ее периметр равен 96.

Найдите площадь этой трапеции.

Видео:Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые #математика #огэ #впрСкачать

В равнобедренной трапеции ABCD высота ВК образует с боковой стороной угол 30°?

В равнобедренной трапеции ABCD высота ВК образует с боковой стороной угол 30°.

А) Найдите углы трапеции ; б) найдите периметр трапеции, если меньшее основание и боковая сторона равны 5 см ; в) докажите, что середины сторон трапеции являются вершинами ромба.

Видео:№746. Основание AD прямоугольной трапеции ABCD с прямым углом A равно 12 смСкачать

Основания трапеции равны 21 и 22, одна из боковых сторон равна , а угол между ней и одним из оснований равен ?

Основания трапеции равны 21 и 22, одна из боковых сторон равна , а угол между ней и одним из оснований равен .

Найдите площадь трапеции.

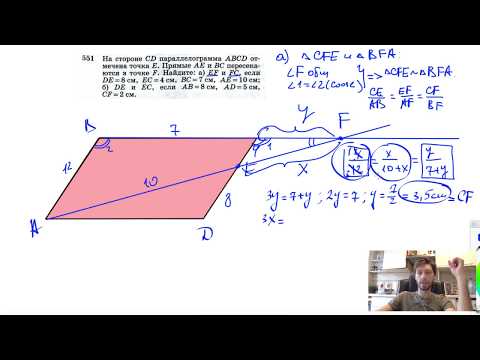
Видео:№551. На стороне CD параллелограмма ABCD отмечена точка Е. Прямые АЕ и ВС пересекаются в точке FСкачать

Основания трапеции равны 3 см и 5 см найдите сумму двух боковых сторон если периметр равен 15 см?

Основания трапеции равны 3 см и 5 см найдите сумму двух боковых сторон если периметр равен 15 см.

На этой странице сайта размещен вопрос Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 13, отсекает треугольник, периметр которого равен 23? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 1 — 4 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

🎦 Видео

Геометрия В трапеции ABCD меньшее основание BC равно 6 см. Через вершину B проведена прямая, котораяСкачать

Планиметрия с нуля и до уровня ЕГЭ 2023 за 4 часа | Вся теория по №1,16 | Математика профильСкачать

Задание 12 (часть 4) | ЕГЭ 2024 Математика (база) | Параллелограмм, трапецияСкачать

Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть II)Скачать

Трапеция. Задачи. Найти углы трапеции. Равнобедренной,прямоугольной,Скачать

Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать

✓ Как решить трапецию | ЕГЭ-2020. Задание 16. Профильный уровень. Основная волна | Борис ТрушинСкачать