Проведем через точку а любую окружность пересекающую прямую l

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Ваш ответ

Видео:Математика 5 класс (Урок№21 - Прямая, луч, отрезок.)Скачать

решение вопроса

Видео:Провести горизонтальную прямую через точку и пересекающую заданный отрезок. Начертательная геометрияСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,036
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Точка встречи прямой с плоскостьюСкачать

Презентация к уроку наглядной геометрии по теме » Параллельность и перпендикулярность»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Параллельность и перпендикулярность

Параллельные и перпендикулярные прямые играют очень большую роль в жизни человека: особенности их взаимного расположения используют в строительстве, технике, искусстве. Теория параллельных занимает одно из центральных мест в науке «геометрия». Именно свойства параллельных прямых определяют основные свойства изучаемого нами пространства.

Рассматривая основные геометрические фигуры, среди всех углов мы выделили прямой угол, равный 90 градусов. Изобразим прямой угол и продолжим его стороны за вершину. ☻ ☻ O В А a b Мы получили две прямые, пересекающиеся под прямым углом. Две прямые, пересекающиеся под прямым углом (90°), называются ПЕРПЕНДИКУЛЯРНЫМИ.

Перпендикулярные прямые обладают интересными свойствами. 1. Через точку вне данной прямой можно провести только одну прямую, перпендикулярную этой прямой и пересекающую ее. 2. Если точку взять на самой прямой, то через эту точку проходит бесконечное число прямых, перпендикулярных данной прямой.

Если начертить прямую в тетради, то одна из прямых, перпендикулярных ей, будет лежать в плоскости тетради, а все остальные прокалывать тетрадь в данной точке. Они будут находиться в пространстве (вне плоскости листа); это похоже на дорожный столб, стоящий на перекрестке дорог: столб перпендикулярен каждой дороге (рис. 2). Рис. 2 Рис. 3 3. Две прямые на плоскости, перпендикулярные третьей прямой, не могут пересечься одна с другой (рис. 3). Если бы они пересеклись, например, в точке С, то мы получили бы треугольник ABC, у которого два прямых угла, что невозможно. На плоскости такого не может быть.

А вот на сфере перпендикуляры ведут себя иначе. Вспомните экватор и меридианы. Они перпендикулярны друг к другу, но все меридианы пересекаются в одной точке — на ПОЛЮСЕ. Однако вернемся к плоскости. Итак, свойство 3 говорит о том, что на плоскости существуют непересекающиеся прямые. Две прямые на плоскости называются ПАРАЛЛЕЛЬНЫМИ, если они не пересекаются. a b

Передвигая, как показано на рисунке, треугольник вдоль неподвижной линейки, получаем множество параллельных между собой прямых. На рисунке 4-в прямые m и n параллельны. Этот факт записывается так: m║n Читаем: прямая m параллельна прямой n Выбор именно такого знака достаточно понятен, не так ли? Рис. 4 а б Используя линейку и чертежный угольник, можно без труда вычерчивать параллельные прямые

У обычного чертежного угольника один угол прямой. В этом случае с его помощью можно проводить прямые, перпендикулярные данной прямой (рис. 5). Или, как говорят, опускать на данную прямую перпендикуляры или восставлять к ней перпендикуляры. То, что прямые m и n перпендикулярны, записывается так: m n. С помощью циркуля и линейки также можно строить параллельные и перпендикулярные прямые. Предлагаемые ниже способы построения интересны и тем, что число проводимых при построении линий будет наименьшим из возможных. Рис. 5

Проведение параллельных прямых Пусть проведена прямая ℓ и дана точка А вне этой прямой (рис. 6). Проведем через точку А любую окружность, пересекающую прямую ℓ (рис. 6). Возьмем одну из точек пересечения окружности с прямой — точку В, измерим циркулем отрезок АВ и проведем окружность радиусом, равным АВ, с центром в точке В1. Появится точка А1. Прямая, проходящая через точки А и А1, параллельна прямой ℓ. Рис. 6

Проведение перпендикуляра к прямой Пусть проведена прямая ℓ и дана точка А вне этой прямой. Для построения перпендикуляра достаточно с помощью циркуля провести через А две произвольные окружности с центрами на прямой ℓ (рис.7). Вторая точка пересечения этих окружностей (точка А1) и даст нам вторую точку на перпендикуляре. Подумайте, как провести перпендикуляр (с помощью циркуля и линейки), если точка А лежит на прямой ℓ… Поэтапное построение

Следует запомнить еще одно важное свойство перпендикуляра. Если А — точка на прямой ℓ, а В — точка пересечения перпендикулярных прямых ℓ и m (рис. 8), то, отрезок АВ есть кратчайшее расстояние от точки А до прямой m ℓ m ☻ A B Рис. 8 Итак, если мы хотим из точки А по кратчайшему пути попасть на прямую m, то двигаться надо по перпендикуляру к прямой m

Мы все время говорили: «параллельные прямые», «перпендикулярные прямые». Понятно, что на практике мы имеем дело не с прямыми, а лишь с их частями — отрезками, лежащими на этих прямых. Отрезки, лежащие на параллельных прямых, также называются ПАРАЛЛЕЛЬНЫМИ, а на перпендикулярных — ПЕРПЕНДИКУЛЯРНЫМИ.

Среди ребер куба можно указать пары параллельных и перпендикулярных ребер. На рисунке 9 изображен куб. Рис. 9 С Три четверки его ребер параллельны между собой. Вот одна из них: АВ || DC || АХВХ || DXCX. 1. Назовите еще две четверки параллельных между собой ребер куба. Ребро АА1 перпендикулярно ребрам АВ, А1В1, AD и A1D1. Угол между ребром АА1 и каждым из этих ребер равен 90°. 2. Назовите ребра, перпендикулярные: а) ребру СС1; б) ребру DC.

Ребра АА1 и ВВ1 куба лежат в одной плоскости — в плоскости передней грани; в этой же плоскости лежат и плоскости передней грани; в этой же плоскости лежат и ребра А1В1 и АВ. Рис. 9 С Через ребра АА1 и СС1 также можно провести плоскость — АА1С1С (диагональное сечение куба).

А вот пара ребер АА1 и D1C1 особенная. Не существует плоскости, которая бы проходила через оба эти отрезка (а также через прямые АА1 и D1C1). Такие отрезки и прямые называются СКРЕЩИВАЮЩИМИСЯ. Какую бы плоскость мы ни провели через АА1, обязательно прямая D1C1 либо пересечет ее в какой-либо одной точке, либо не пересечет никогда. 3. Найдите еще несколько пар скрещивающихся ребер куба AC1. С Обозначение: a b ☻ Читают: прямые a и b — скрещивающиеся

За 5 мин привести как можно больше примеров: 1) параллельных прямых 2) перпендикулярных прямых, встречающихся в окружающем нас мире. Участники поочередно называют примеры таких прямых. Игра заканчивается, как только в течение минуты никто не может придумать новый пример. Побеждает тот, чей пример был последним.

Найдите на рисунке 9 какие-либо отрезки с концами в вершинах куба (не являющиеся его ребрами), такие, чтобы они были: а) параллельными; б) перпендикулярными; в) скрещивающимися. С

Домашнее задание Выполнить все построения, которые выполняли на уроке, выделяя цветом главные этапы и линии, на альбомном листе А-4.

Спасибо за внимание! Желаю удачных построений параллельных и перпендикулярных прямых!

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 1008 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 682 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 315 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Отрезок, луч, прямаяСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 532 191 материал в базе

Другие материалы

• 31.08.2016
• 4363
• 92

• 31.08.2016
• 1477
• 29

• 31.08.2016
• 497
• 0

• 31.08.2016
• 2894
• 67

• 31.08.2016
• 1482
• 0

• 31.08.2016
• 2118
• 5

• 31.08.2016
• 10985
• 125

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 31.08.2016 3965
• PPTX 1.1 мбайт
• 155 скачиваний
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Адеева Галина Витальевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 2 года и 4 месяца
• Подписчики: 0
• Всего просмотров: 63173
• Всего материалов: 26

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Перпендикуляр к прямой через заданную точку.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Студенты на Северном Кавказе бесплатно подготовят к ЕГЭ сельских школьников

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В Тюменской области школы и колледжи перевели на дистанционное обучение

Время чтения: 1 минута

Ставропольских школьников с 1 по 8 класс перевели на дистанционное обучение

Время чтения: 2 минуты

Минтруд рекомендовал перевести на удаленку максимальное число сотрудников

Время чтения: 1 минута

В Курганской области школьников переведут на дистанционное обучение с 4 февраля

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Решаем задачи на построение — часть 3

Продолжаем рассматривать элементарные геометрические построения.

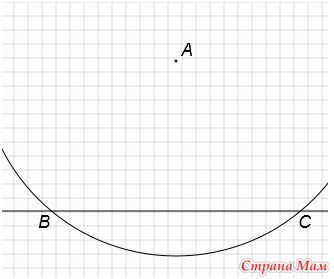
5. Построить прямую, проходящую через данную точку и перпендикулярную данной прямой
Проведём окружность с центром в точке А таким радиусом, чтобы она пересекла прямую а в двух точках. Назовём их В и С.

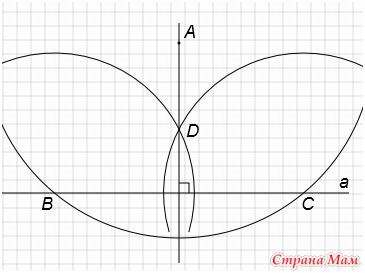
С центром в точке В проведем окружность радиусом больше половины длины отрезка ВС.
C центром в точке С этим же радиусом проведём окружность. Получим точку D.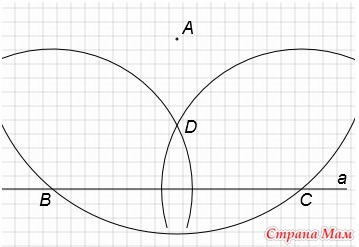

Через точки А и D проведём прямую. Она будет являться перпендикуляром к прямой а.

6. Построить прямую, проходящую через данную точку и параллельную данной прямой
Полагаем, что нам дана прямая а и точка К, не лежащая на прямой а.
Выбираем произвольную точку Т, не лежащую на прямой а и отличную от точки К. Проводим через точку Т перпендикуляр к прямой а (смотри элементарное построение №5), обозначим его прямой b. Через точку К проводим перпендикуляр к прямой b (смотри элементарное построение №5). Построенный перпендикуляр — прямая, параллельная данной прямой.

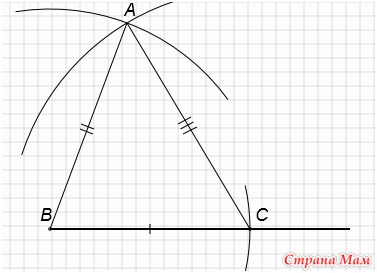
7. Построить треугольник по трем данным сторонам
Дано: отрезок а, отрезок в, отрезок с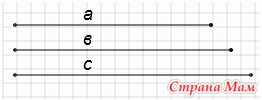

Построим произвольно луч.
Отложим на луче отрезок, равный отрезку а. Для этого сделаем раствор циркуля равным длине отрезка а и проведем окружность с центром в начале луча этим радиусом. Получим точки точки В и С.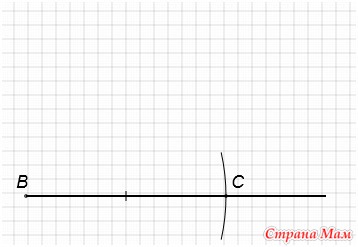

C центром в точке В проведем окружность радиусом равным длине отрезка в.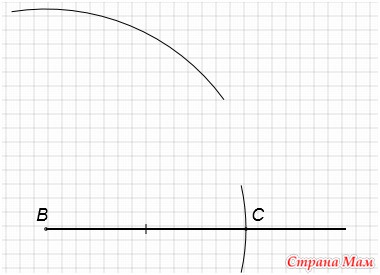

C центром в точке C проведем окружность радиусом равным длине отрезка c. Получим точку А.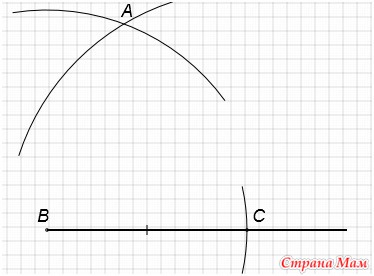

Соединим точку А с точками В и С. Получим треугольник АВС.

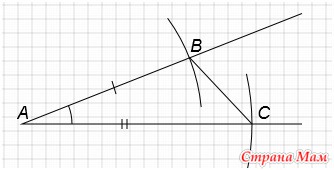
8. Построить треугольник по двум сторонам и углу между ними
Дано: отрезок а, отрезок b, угол A1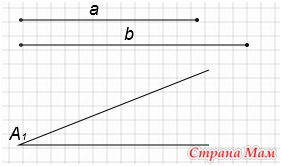

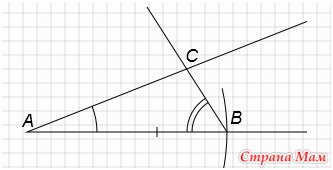
Построим угол А, равный углу А1 (Смотри элементарное построение №4).
С центром в точке А проведем окружность радиусом равным длине отрезка а. Получим точку В.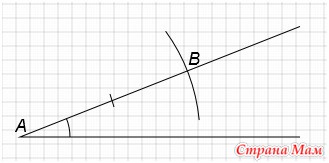

С центром в точке А проведем окружность радиусом равным длине отрезка b. Получим точку C.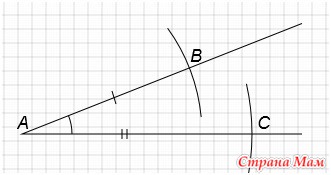

Соединим точки В и С. Получим треугольник АВС.

9. Построить треугольник по стороне и двум углам, прилежащим к ней
Дано: отрезок а, угол А1, угол В1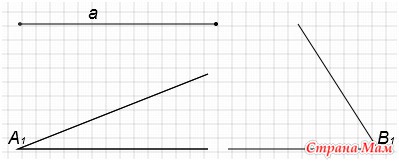

Построим угол А, равный углу А1. (Смотри элементарное построение №4).
С центром в точке А проведем окружность радиусом равным длине отрезка а. Получим точку В.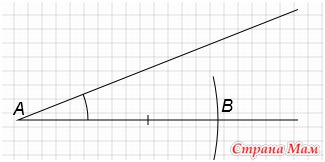

C вершиной в точке В строим угол, равный углу В1. Получим точку С. Получили треугольник АВС.

Удачи в решении задач!
Спасибо за внимание.

🎦 Видео

№11. Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие черезСкачать

Проецирование прямой общего положенияСкачать

Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Геометрия 7 класс Урок 3 Точка Прямая ПлоскостьСкачать

Пересечение прямой линии с плоскостью Определение видимости прямойСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Построение окружности по трём точкам.Скачать

Окружность и задачи на построениеСкачать

ЗАДАЧИ НА ПОСТРОЕНИЕ. §22 геометрия 7 классСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Лекция 2. Основная задача начертательной геометрии. Точка пересечения прямой с плоскостью.Скачать

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать