Программа для деления окружности на части скачать (2 видео)

Деление круга на равные части

Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами

Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.

Содержание

Деление круга на равные по площади части радиусами
Деление круга на равные по площади части параллельными хордами
Деление круга на равные части радиусами
Деление круга на равные части параллельными хордами
Программа Segment
Деление окружности на любое количество равных частей в КОМПАС — 3D с примером
📺 Видео

Деление круга на равные по площади части радиусами

Деление круга на равные по площади части параллельными хордами

Деление круга на равные части радиусами

Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:

Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.

Определяем размер дуги сектора, перемножая радиус на угол в радианах

Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.

Собственно и всё — мы получили все характеристики для N равных секторов

Деление круга на равные части параллельными хордами

Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.

Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.

Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.

По теореме Пифагора получаем следующую функцию

Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:

Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем

Итак, полное выражение

Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)

Таким образом мы можем приравнять

Что дает нам такое финальное уравнение

Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.

Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.

Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.

Видео:Деление окружности на равные части. Внимание!!! В таблице имеются ошибки. ПОЛЬЗУЙТЕСЬ ФОРМУЛОЙ!!!Скачать

Программа Segment

Программа Segment предназначена для вычисления геометрических параметров сегмента круга. В расчетах участвуют пять величин:

диаметр круга,
длина дуги,
длина хорды,
центральный угол,
высота сегмента,

любые две из которых задаются, а оставшиеся вычисляются.

Дополнительно вычисляются значения:

длины окружности,
площади круга,
площади сегмента,
площади сектора,

соответствующие заданным величинам.

Теоретическая сторона вычислений описана в статье Геометрия круга.

Программа очень пригодится людям, проектирующим что-нибудь круглое. Например, ювелирам для разработки эскизов колец, браслетов и прочей ерунды.

Segment рассчитана на выполнение под Windows (XP, 7, 8, 10) и не требует специальной установки. Нужно просто извлечь из архива два файла и поместить их в одну папку.

Segment.exe — выполняемый файл;
SegmentHelp.chm — файл справки, который открывается не только из программы, но и отдельно, так что вы можете изучить его еще до запуска программы.

Для удаления программы — просто удалить эти файлы.

Программа распространяется бесплатно и не содержит рекламы.

Примечание 1. Если у программы возникнут проблемы с системой безопасности Windows, то обратитесь к статье Как скачать программу.

Примечание 2. Если при запуске программы вы получаете сообщение, содержащее название .NET Framework, то обратитесь к статье Что такое .NET Framework.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Деление окружности на любое количество равных частей в КОМПАС — 3D с примером

Деление окружности на любое количество равных частей:

Чтобы выполнить шестое задание «Деление окружности на равные части» составим алгоритм последовательности выполнения работы:

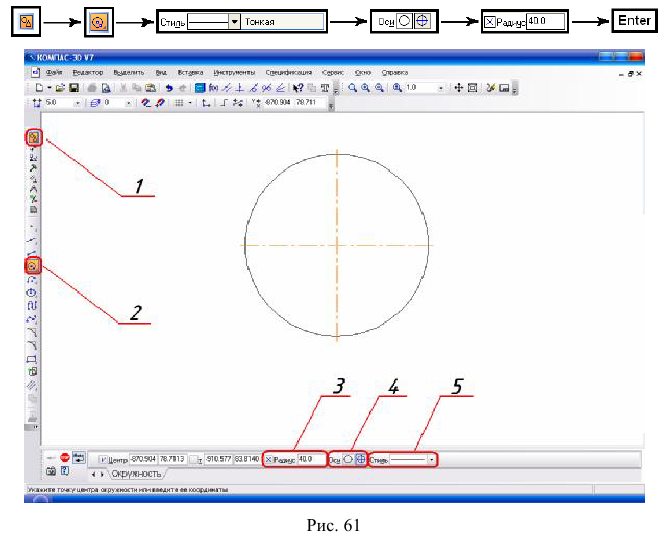
1) построить окружность (радиус 40 мм);
2) разделить окружность на равные части, допустим на 7;
3) построить вписанный в окружность семиугольник.

1. Построение окружности радиусом 40 мм. Войдите на страницу Геометрия (1)

Алгоритм построения выглядит следующим образом:

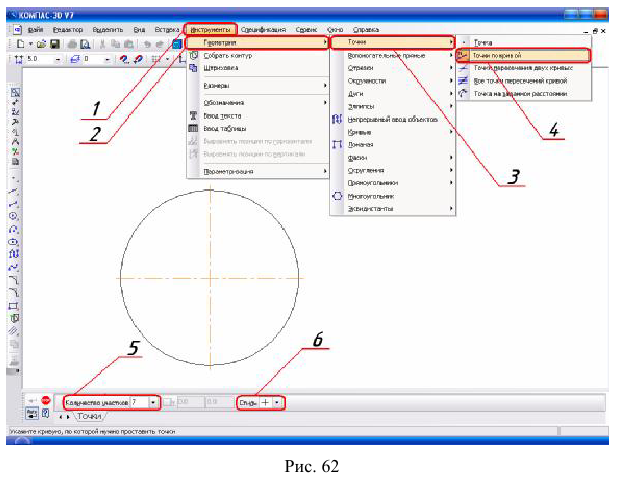
2. Деление окружности на 7 равных частей. Имея готовую окруж-

ность войдите в Строку меню (1) и щелчком левой кнопки мыши вызовите каскадное меню. Затем в Строке параметров (внизу рабочего поля) укажите Количество участков в данном случае 7 и выберите Стиль точки (рис. 62).

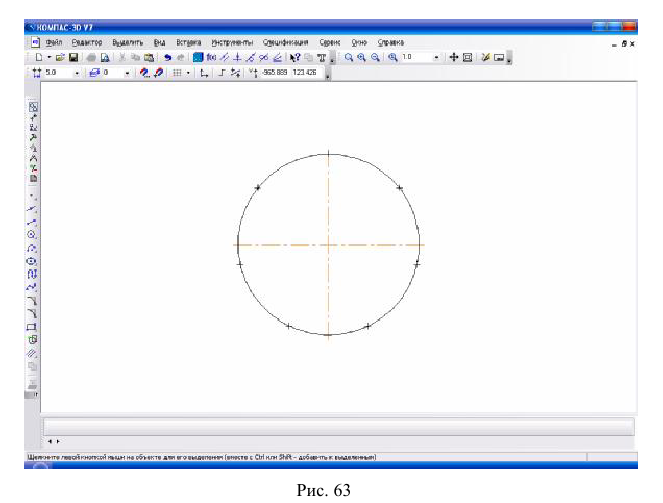
На рис. 63 показана окружность, поделённая на 7 равных частей.

Таким же образом можно построить деление окружности на любое количество равных частей.

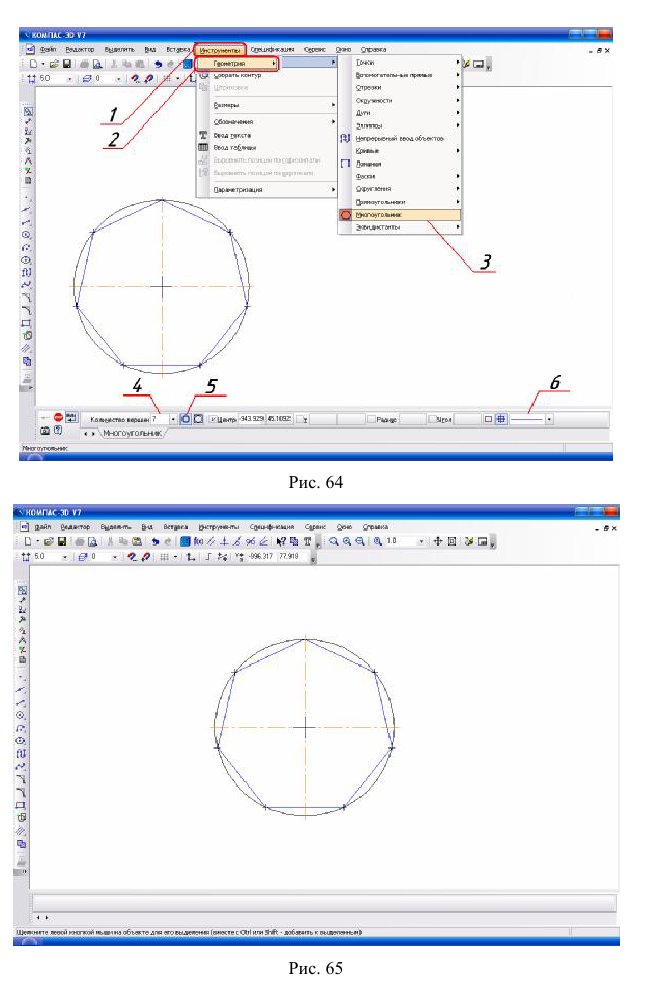
3. Построение семиугольника, вписанного в окружность. В заданную окружность можно вписать многоугольник.

Команда «Многоугольник» (3)из каскадного меню позволяет построить многоугольники с любым количеством вершин. Рассмотрим построение семиугольника.

Чтобы построить семиугольник необходимо следовать указаниям, приведённым ниже.

Войдите в Строку меню (1)и щелчком левой кнопки мы-
ши вызовите каскадное меню. После выбора команды «Многоуголь-
ник» (5)из каскадного меню на экране автоматически появляется
Строка параметров, в которой укажите Количество вершин

в данном случае 7, выберите многоугольник «По описанной окружности »и укажите «Стиль линии»(рис 64)
Алгоритмы для построения семиугольника:

На рис. 65 — семиугольник, вписанный в окружность.

Рекомендую подробно изучить предметы:

Инженерная графика
Начертательная геометрия
Компас
Автокад
Черчение
Проекционное черчение
Аксонометрическое черчение
Строительное черчение
Техническое черчение
Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

Алгоритм построения контура технической детали с сопряжениями в КОМПАС — 3D
Алгоритм построения двутавра в КОМПАС — 3D
Создание модели зубчатой шестерни раздаточного редуктора рабочего рольганга в КОМПАС — 3D
Создание моделей деталей раздаточного редуктора с использованием вариационной параметризации в КОМПАС — 3D
Деление отрезка прямой на любое число равных частей в КОМПАС — 3D
Деление угла на две равные части в КОМПАС — 3D
Деление прямого угла на три равные части в КОМПАС — 3D
Построение угла, равного заданному в КОМПАС — 3D

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.