Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами
Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.
- Деление круга на равные по площади части радиусами
- Деление круга на равные по площади части параллельными хордами
- Деление круга на равные части радиусами
- Деление круга на равные части параллельными хордами
- Деление окружности на любое количество равных частей в КОМПАС — 3D с примером
- Bau-enginer
- Деление окружности на равные части
- 📸 Видео
Деление круга на равные по площади части радиусами
Деление круга на равные по площади части параллельными хордами
Деление круга на равные части радиусами
Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:
- Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.
- Определяем размер дуги сектора, перемножая радиус на угол в радианах
- Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.
Собственно и всё — мы получили все характеристики для N равных секторов
Деление круга на равные части параллельными хордами
Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.
Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.
Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.
По теореме Пифагора получаем следующую функцию
Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:
Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем
Итак, полное выражение
Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)
Таким образом мы можем приравнять
Что дает нам такое финальное уравнение
Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.
Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.
Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.
Видео:Деление окружности на 3; 6; 12 равных частейСкачать
Деление окружности на любое количество равных частей в КОМПАС — 3D с примером
Деление окружности на любое количество равных частей:
Чтобы выполнить шестое задание «Деление окружности на равные части» составим алгоритм последовательности выполнения работы:
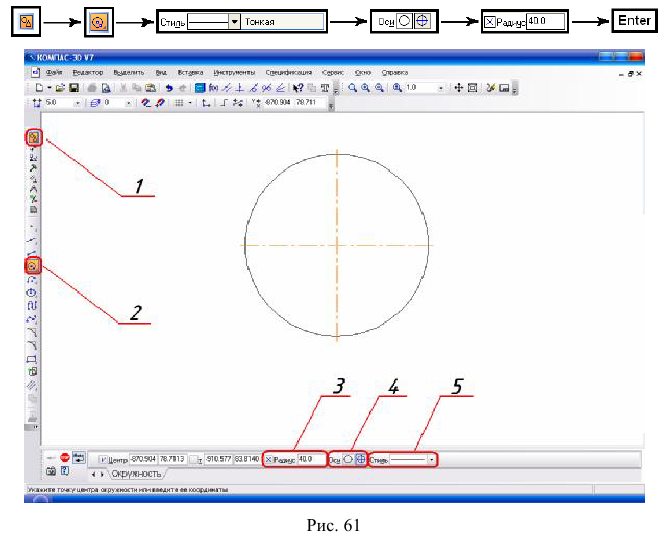
- 1) построить окружность (радиус 40 мм);
- 2) разделить окружность на равные части, допустим на 7;
- 3) построить вписанный в окружность семиугольник.
1. Построение окружности радиусом 40 мм. Войдите на страницу Геометрия (1)
Алгоритм построения выглядит следующим образом:
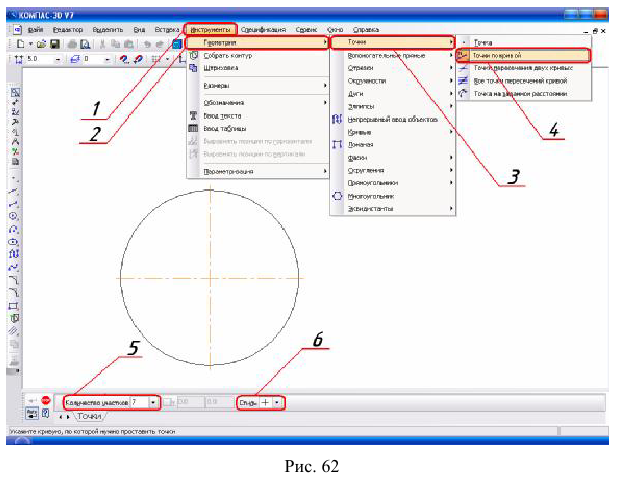
2. Деление окружности на 7 равных частей. Имея готовую окруж-
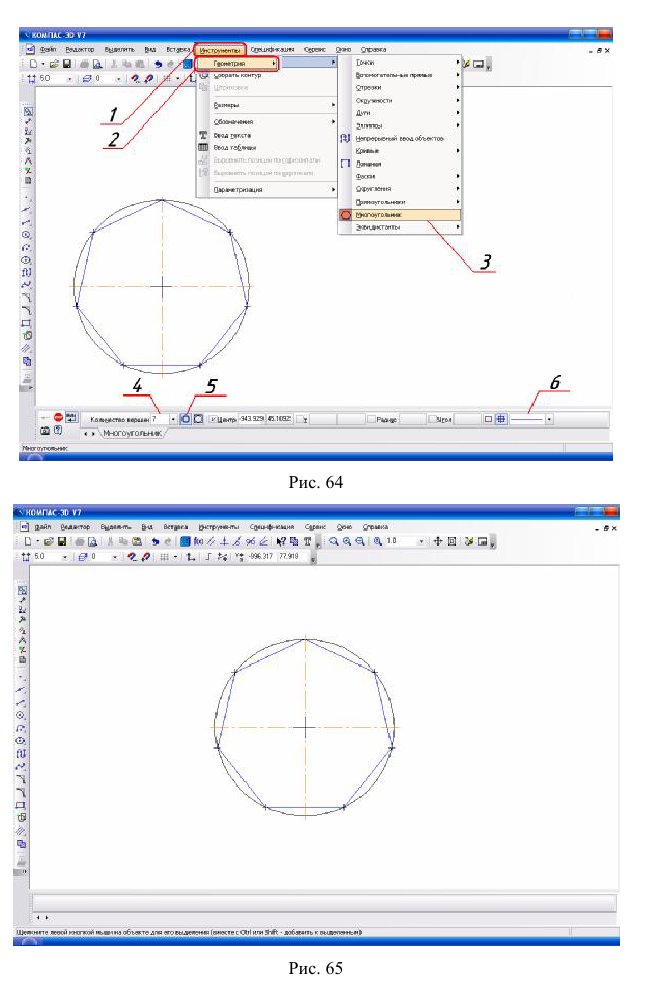
ность войдите в Строку меню (1) 
и щелчком левой кнопки мыши вызовите каскадное меню. Затем в Строке параметров (внизу рабочего поля) укажите Количество участков 
в данном случае 7 и выберите Стиль точки 
(рис. 62).
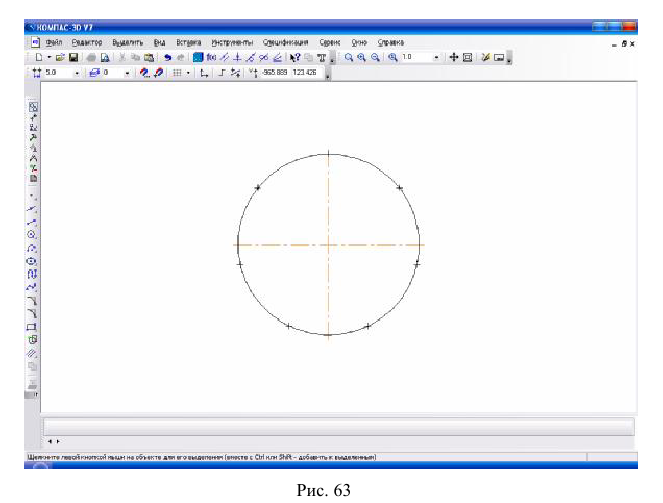
На рис. 63 показана окружность, поделённая на 7 равных частей.
Таким же образом можно построить деление окружности на любое количество равных частей.
3. Построение семиугольника, вписанного в окружность. В заданную окружность можно вписать многоугольник.
Команда «Многоугольник» (3)
из каскадного меню позволяет построить многоугольники с любым количеством вершин. Рассмотрим построение семиугольника.
Чтобы построить семиугольник необходимо следовать указаниям, приведённым ниже. 
Войдите в Строку меню (1)
и щелчком левой кнопки мы-
ши вызовите каскадное меню. После выбора команды «Многоуголь-
ник» (5)
из каскадного меню на экране автоматически появляется
Строка параметров, в которой укажите Количество вершин
в данном случае 7, выберите многоугольник «По описанной окружности »
и укажите «Стиль линии»
(рис 64)
Алгоритмы для построения семиугольника:
На рис. 65 — семиугольник, вписанный в окружность.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Алгоритм построения контура технической детали с сопряжениями в КОМПАС — 3D
- Алгоритм построения двутавра в КОМПАС — 3D
- Создание модели зубчатой шестерни раздаточного редуктора рабочего рольганга в КОМПАС — 3D
- Создание моделей деталей раздаточного редуктора с использованием вариационной параметризации в КОМПАС — 3D
- Деление отрезка прямой на любое число равных частей в КОМПАС — 3D
- Деление угла на две равные части в КОМПАС — 3D
- Деление прямого угла на три равные части в КОМПАС — 3D
- Построение угла, равного заданному в КОМПАС — 3D
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Деление окружности на равные части. Внимание!!! В таблице имеются ошибки. ПОЛЬЗУЙТЕСЬ ФОРМУЛОЙ!!!Скачать
Bau-enginer
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
| « Май | ||||||
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | |
Видео:Деление окружностей на равные частиСкачать
Деление окружности на равные части
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
В данной статье Вы узнаете как разделить окружность на 3-6, 4-8, 5-10 и n частей.
Как разделить окружность на 3 и 6 частей
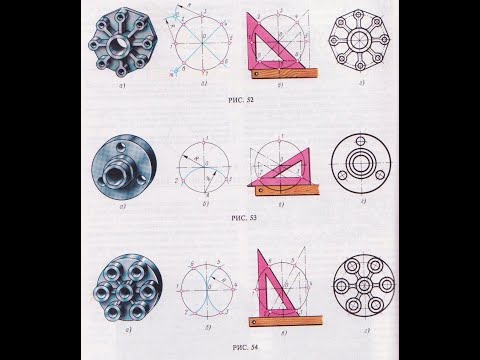
Для деления окружности на 3, 6 и кратное им количество частей проводим окружность заданного радиуса и со ответствующие оси. Деление можно начинать от точки пересечения вертикальной или горизонтальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6 раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шестиугольник. Соединение точек через однудает равносторонний треугольник, и деление окружности на 3 равные части.
Деление окружности на 3-6 равных частей
Как разделить окружность на 5 и 10 частей
Для того чтобы разделить окружность на 5 и 10 равных частей необходимо построить правильный пятиугольник. Для его построения необходимо выполнить следующее. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т. 5) и получают сторону правильного пятиугольника, затем откладывают полученное расстояние по окружности 5 раз до получения правильного пятиугольника. Расстояние «b-0» дает сторону правильного пятиугольник.
Деление окружности на 5-10 равных частей
Как разделить окружность на n — равных частей
Иначе необходимо построить правильный многоугольник с n количеством сторон. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1″ окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей, на которые мы делим данную окружность, например 9 . Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Провод им линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через четные (или нечетные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т. к. точки 1, 2,… 9 делят окружность на 9 (N) равных частей.
Деление окружности на n равные части
Деление окружности на произвольное число равных частей можно производить с помощью таблицы хорд, численное выражение которых определяется умножением радиуса данной окружности на коэффициент, соответствующий числу деления, представленный в таблице.
Таблица хорд (коэффициентов для деления окружности)
| Число частей делений окружности | Коэффициент | Число частей делений окружности | Коэффициент | Число частей делений окружности | Коэффициент |
| 1 | 0,000 | 11 | 0,282 | 21 | 0,149 |
| 2 | 1,000 | 12 | 0,258 | 22 | 0,142 |
| 3 | 0,866 | 13 | 0,239 | 23 | 0,136 |
| 4 | 0,707 | 14 | 0,223 | 24 | 0,130 |
| 5 | 0,588 | 15 | 0,208 | 25 | 0,125 |
| 6 | 0,500 | 16 | 0,195 | 26 | 0,120 |
| 7 | 0,434 | 17 | 0,184 | 27 | 0,116 |
| 8 | 0,383 | 18 | 0,178 | 28 | 0,112 |
| 9 | 0,342 | 19 | 0,165 | 29 | 0,108 |
| 10 | 0,309 | 20 | 0,156 | 30 | 0,104 |
Как найти центр дуги окружности
Необходимо выполнить следующее: на данной дуге отмечаем четыре произвольные точки A, B, C, D и соединяем их попарно хордами AB и CD.
Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров дает центр данной дуги и соответствующей ей окружности.
Приближенное деление дуги окружности на произвольное число равныx частей можно выполнить при помощи циркуля методом последовательного приближения.
📸 Видео
Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
1 2 2 деление окружности на 5 равных частейСкачать
Деление окружности на 3 частиСкачать
Видеоуроки по КОМПАС 3D. Урок 1 Деление окружности на равные частиСкачать
Деление окружности на 12 равных частейСкачать
Деление окружности на N равных частей. Урок 8. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
Деление окружности на n- равные частиСкачать
Деление окружности на 5 частейСкачать
деление окружности на произвольное число частейСкачать
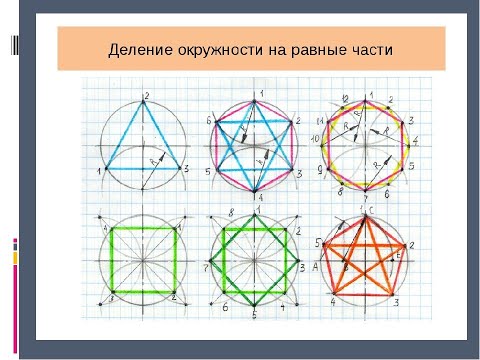
Деление окружности на равные частиСкачать
Деление окружности на 5 равных частейСкачать
Деление окружности на равные части с помощью циркуляСкачать
Деление окружности на 6 равных частейСкачать
Деление окружности на 4 частиСкачать
Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать
Деление окружности на равные части в CorelDRAW (2)Скачать
