Проекция окружности на плоскость под углом (7 видео)

Проецирование окружности

Окружность с центром О, рассматриваемая как плоская фигура, проецируется без искажения на ту плоскость, которой она параллельна (рис. 6.5). При этом две другие ее проекции есть отрезки, параллельные осям проекций и равные по длине диаметру окружности.

Если окружность наклонена к плоскости проекций, то ее проекция представляет собой эллипс, большая ось которого равна диаметру окружности. Величина малой оси зависит от угла наклона плоскости окружности к плоскости проекций.

Окружность, изображенная на рис. 6.6, перпендикулярна плоскости проекций П и наклонена к плоскости проекций к₂, поэтому ее фронтальная проекция — эллипс. Большая ось этого эллипса С «И « представляет собой проекцию диаметра окружности, который без искажения проецируется на плоскость проекций л₂. Таким образом, она перпендикулярна плоскости проекций Л1 и параллельна плоскостям проекций 7^2 и Лз. Малая ось эллипса является проекцией диаметра АВ, перпендикулярного СИ. Ее величину на плоскости проекций п₂ определяют с помощью линий проекционной связи, проведенных через точки А’ и В’.

Промежуточные точки эллипса находят с помощью дополнительной плоскости проекций тс₄, которую располагают параллельно плоскости окружности, поэтому окружность проецируется на нее без искажения. Вначале строят новую проекцию центра окружности — точку О™ и на плоскости тс₄ описывают заданную окружность. Затем на окружности намечают 8 или 12 произвольных точек и находят их проекции в системах плоскостей щ/щ и щ/л₂. На рис. 6.6 приведено построение только для двух промежуточных точек 1 и 2; остальные строят аналогично.

Окружность, расположенная в плоскости общего положения, проецируется на все основные плоскости проекций в виде эллипсов, большие оси которых равны ее диаметру. Величины малых осей обычно различны и зависят от углов

наклона заданной плоскости, в которой расположена окружность, к плоскостям проекций.

Если эллипс представляет собой проекцию окружности, то на горизонтальной проекции его большая ось расположена на горизонтальной прямой плоскости, на фронтальной — на фронтальной прямой и на профильной — на профильной прямой.

Построение в плоскости общего положения а(И_а п /_а) (рис. 6.7) проекций окружности с центром в точке О, расположенной на горизонтальной прямой /г_а, и с радиусом, равным /?, начинают с определения проекций осей эллипса.

На горизонтальной проекции окружности по прямой /г_а‘ вправо и влево от точки О‘ откладывают радиус окружности Л, получая при этом точки А’ я В’. Сделав замену плоскостей проекций щ/л2 —> п/щ, где п₄_1_ И_а, и построив новую проекцию окружности в виде отрезка С ,У /) |У , равного диаметру окружности, строят с помощью точек С’ и /)’ малую ось эллипса на горизонтальной проекции (направления построений указаны стрелками).

Для фронтальной проекции окружности через точку О « проводят проекцию прямой, параллельной^’, и на ней вправо и влево от точки О » откладывают радиус окружности Я, получая точки Е «, Е». Сделав замену плоскостей проекций П/П2 —> П2/Л5, где п₅ Е/_а, и построив новую проекцию окружности в виде отрезка, равного диаметру окружности, строят на фронтальной проекции с помощью точек 1У, малую ось эллипса.

Таким образом, на каждой проекции есть по четыре точки, принадлежащие проекции окружности: точки Л ‘, ВС‘, В‘ и Е «, Е», К «, Ь». Проводя из них линии проекционной связи, получают восемь точек для построения горизонтальной и фронтальной проекций эллипса.

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Построение проекций окружности

При выполнении чертежей деталей нередко возникает необходимость изображения окружностей, плоскости расположения которых не параллельны плоскостям проекций. Например, на рис. 7.13 окружность расположена в пространстве в плоскости β. В этом случае окружность проецируется в эллипс, а любая пара ее взаимно перпендикулярных диаметров проецируется парой сопряженных диаметров эллипса. Диаметр (1–2) окружности, параллельной плоскости проекций, проецируется без искажения и является для эллипса-проек-

ции большой осью (отрезок Iй2°). Остальные диаметры проецируются отрезками меньшей длины. Диаметр 3–4, перпендикулярный диаметру 1–2, проецируется как малая ось 3°4° эллипса: (1–2) 1 (3–4), (1–2) | π, следовательно, (3°4°) J.(I02°).

Пример построения горизонтальной проекции окружности, расположенной во фронтально проецирующей плоскости, приведен на рис. 7.14. Фронтальная проекция Г’0″2″ окружности совпадает с фронтальной проекцией а» фронтально проецирующей плоскости. Фронтальная проекция 3” ≡ 4″ диаметра окружности, перпендикулярного плоскости проекции π2, совпадает с фронтальной проекцией О « центра окружности. Горизонтальная проекция 3 ‘4’ этого диаметра, проецирующегося без искажения, является большой осью эллипса-проекции. Диаметр с фронтальной проекцией 7 «2» на горизонтальной проекции является малой осью 1 ‘2’ эллипса-проекции. На горизонтальной проекции показано построение одной из произвольных точек эллипса-проекции.

Пример построения проекций окружности, расположенной в плоскости общего положения, приведен на рис. 7.15. Плоскость задана проекциями А «О « и А ‘0’фронтали и В»О” и В’О’ горизонтали, пересекающимися в центре окружности с проекциями О «, О

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Построение окружности в начертательной геометрии с примером

Построение окружности:

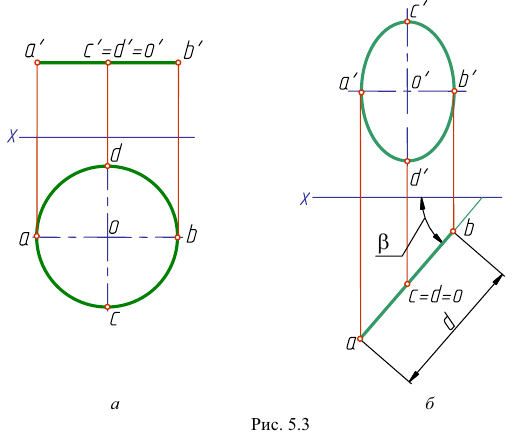
Окружность — плоская кривая второго порядка, ортогональная проекция которой может быть окружностью и эллипсом (рис. 5.3).

Для изображения окружности диаметра d на комплексном чертеже обязательно строят проекции центра О и двух ее диаметров.

Если окружность расположена в плоскости уровня, например в плоскости, параллельной плоскости Н (рис. 5.3, а), то в этом случае фронтальной проекцией окружности служит отрезок, равный d, а гори зонтальной проекцией является окружность.

Если окружность расположена в проецирующей плоскости, то проекции ее диаметров параллельны плоскостям проекций. Например,

Если окружность расположена в плоскости общего положения, она проецируется на все плоскости проекций в виде эллипсов, которые можно построить по сопряженным диаметрам. Эти диаметры являются проекциями диаметров, параллельных плоскостям проекций.

Рекомендую подробно изучить предметы:

Инженерная графика
Начертательная геометрия
Компас
Автокад
Черчение
Проекционное черчение
Аксонометрическое черчение
Строительное черчение
Техническое черчение
Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

Цилиндрическая винтовая линия
Определение и задание поверхностей на чертеже
Классификация поверхностей
Пересечение многогранников плоскостями
Взаимное положение двух плоскостей, прямой линии и плоскости
Решение задач на тему: перпендикулярности прямой и плоскости
Проекции с числовыми отметками
Перспектива

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.