Признак параллельных прямых по накрест лежащим углам (8 видео)

Прямая линия. Признаки параллельности прямых линий.

Если две произвольные прямые AB и СD пересечены третьей прямой MN, то образовавшиеся при этом углы получают попарно такие названия:

соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;

внутренние накрест лежащие углы: 3 и 5, 4 и 6;

внешние накрест лежащие углы: 1 и 7, 2 и 8;

внутренние односторонние углы: 3 и 6, 4 и 5;

внешние односторонние углы: 1 и 8, 2 и 7.

Описанные углы видны на рисунке:

Теорема.

Если две параллельные прямые пересечены третьей прямой, то сформировавшиеся:

1. внутренние накрест лежащие углы одинаковы;

2. внешние накрест лежащие углы одинаковы;

3. соответственные углы одинаковы;

4. сумма внутренних односторонних углов будет 2d = 180 0 ;

5. сумма внешних односторонних углов будет 2d = 180 0 ;

Данную теорему иллюстрирует рисунок:

Имеются две параллельные прямые AB и СD, их пересекает третья прямая MN.

1. ∠ 4 = ∠ 6 и ∠ 3 = ∠ 5;

2. ∠ 2 = ∠ 8 и ∠ 1 = ∠ 7;

3. ∠ 2 =∠ 6, ∠ 1 = ∠ 5, ∠ 3 = ∠ 7, ∠ 4 = ∠ 8;

4. ∠ 3 + ∠ 6 = 2d и ∠ 4 + ∠ 5 = 2d;

5. ∠ 2 + ∠ 7 = 2d и ∠ 1 + ∠ 8 = 2d.

1. Из середины E того отрезка прямой MN, который размещается между параллельными прямыми, прочертим на СD перпендикуляр EK и продолжим его до пересечения с AB в точке L. Так как перпендикуляр к одной из параллельных есть также и перпендикуляр к другой параллельной, то образовавшиеся при этом треугольники (заштрихованные на чертеже) — оба прямоугольные. Они одинаковы, потому что в них по равной гипотенузе и по одинаковому острому углу при точке E. Из равенства треугольников получаем, что внутренние накрест лежащие углы 4 и 6 одинаковы. Два прочих внутренних накрест лежащих угла 3 и 5 одинаковы, как дополнения до 2d к одинаковым углам 4 и 6 (как смежные с 4 и 6).

2. Внешние накрест лежащие углы равны соответственно внутренним накрест лежащим углам, как углы вертикальные.

Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6.

Следовательно, ∠ 2 =∠ 8.

3. Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.

4. Сумма внутренних односторонних углов 3 и 6 будет 2d, потому что сумма смежных углов 3 и 4 равна 2d = 180 0 , а ∠ 4 можно заменить идентичным ему ∠ 6. Также убедимся, что сумма углов 4 и 5 равна 2d.

5. Сумма внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам, как углы вертикальные.

Из выше доказанного обоснования получаем обратные теоремы.

Когда при пересечении двух прямых произвольной третьей прямой получим, что:

1. Внутренние накрест лежащие углы одинаковы;

или 2. Внешние накрест лежащие углы одинаковые;

или 3. Соответственные углы одинаковые;

или 4. Сумма внутренних односторонних углов равна 2d = 180 0 ;

или 5. Сумма внешних односторонних равна 2d = 180 0 ,

Содержание

Геометрия. 7 класс
Признаки параллельности прямых
Углы, образующиеся при пересечении двух прямых третьей прямой
Признаки параллельности двух прямых
🎥 Видео

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Геометрия. 7 класс

Конспект урока

Признаки параллельности прямых

Перечень рассматриваемых вопросов:

Параллельные прямые.
Накрест лежащие, соответственные, односторонние углы.
Признаки параллельности прямых.
Решение задач на доказательство параллельности прямых.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Признаки параллельности двух прямых:

1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Вы уже знаете, что при пересечении двух прямых секущей образуются углы:

накрест лежащие: 3 и 6, 4 и 5.
односторонние: 3 и 5, 4 и 6.
соответственные: 1 и 5, 3 и 7, 2 и 6; 4 и 8.

Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

Рассмотрим и докажем признаки параллельности прямых.

Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.

В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.

2 случай: ∠ 1= ∠ 2 ≠ 90°

1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH₁, равный отрезку AH и проведем отрезок OH₁.

2) AO = OB т. к. O середина AB; AH = BH₁ по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH₁B по первому признаку равенства треугольников.

Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.

3) Из равенства углов ∠3 и ∠4 следует, что точка H₁ лежит на продолжении луча OH. Это значит, что точки H₁, O, H лежат на одной прямой.

4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН₁, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.

Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.

∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.

Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.

∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.

∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.

Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Разбор заданий тренировочного модуля.

Дано: ∠1= 60°, ∠2 = 120°.

∠2 и ∠3 смежные, ∠3 = 180° – 120° = 60° по свойству смежных углов;
∠3 = ∠1, это накрест лежащие углы;
Значит, прямые a и b параллельны по 1 признаку параллельности прямых.

Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.

Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.

Докажите: AB ║ CD.

∠A = ∠C = 60° – углы при основании равнобедренного Δ–ка равны.
∠BCK и ∠С смежные. ∠BCK = 180° – 60°= 120° – по свойству смежных углов.
∠BCD = ∠CDK = 60° т. к. CD – биссектриса делит угол пополам.
Значит, ∠A = ∠DCK = 60° ‑ соответственные, следовательно, AB║CD по 2 признаку параллельности прямых.

Ответ: AB║CD по 2 признаку параллельности прямых.

Видео:Теорема 14.1 Если накрест лежащие углы равны, то прямые параллельныСкачать

Признаки параллельности прямых

При пересечении двух прямых третьей прямой образуются углы, названия которых приведены в следующей таблице.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Углы, образующиеся при пересечении двух прямых третьей прямой

Рисунок	Определение углов
	Внутренние накрест лежащие углы
	Внутренние накрест лежащие углы
	Внешние накрест лежащие углы
	Внешние накрест лежащие углы
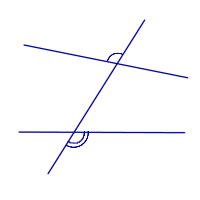	Соответственные углы



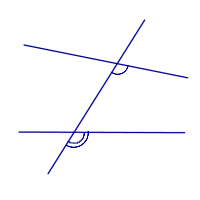	Внутренние односторонние углы
	Внутренние односторонние углы
	Внешние односторонние углы
	Внешние односторонние углы

Внутренние накрест лежащие углы

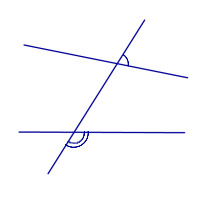Признак параллельных прямых по накрест лежащим углам

Внешние накрест лежащие углы

Соответственные углы

Внутренние односторонние углы

Внешние односторонние углы

Перечисленные в таблице углы используются в формулировках признаков параллельности двух прямых.

Определение . Две прямые на плоскости называются параллельными, если они не имеют общих точек.

Замечание . Два отрезка называются параллельными , если они лежат на параллельных прямых.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Признаки параллельности двух прямых

Рисунок	Признак параллельности
	Прямые параллельны тогда и только тогда, когда внутренние накрест лежащие углы равны

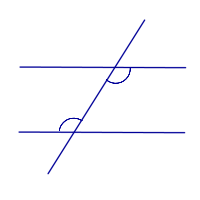	Прямые параллельны тогда и только тогда, когда внешние накрест лежащие углы равны

	Прямые параллельны тогда и только тогда, когда соответственные углы равны



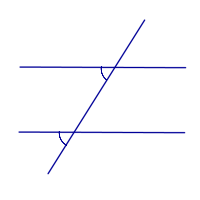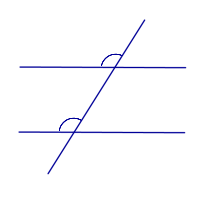	Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°

	Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°

Прямые параллельны тогда и только тогда,
когда внутренние накрест лежащие углы равны

Прямые параллельны тогда и только тогда,
когда внешние накрест лежащие углы равны

Прямые параллельны тогда и только тогда,
когда соответственные углы равны

Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°

Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°

Рисунок	Признак параллельности
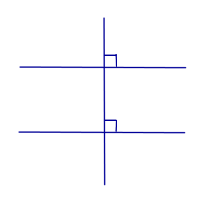	Две прямые, перпендикулярные к третьей прямой, параллельны

Две прямые, перпендикулярные к третьей прямой, параллельны

Переход свойства параллельности прямых

Рисунок	Признак параллельности
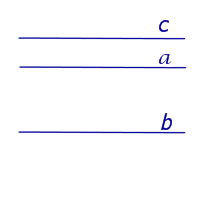	Если прямая a параллельна прямой b , а прямая b параллельна прямой c , то прямая a параллельна прямой c

Если прямая a параллельна прямой b ,
а прямая b параллельна прямой c ,
то прямая a параллельна прямой c

Задача . Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.

Решение . Решение этой задачи почти дословно совпадает с решением задачи из раздела нашего справочника «Углы на плоскости» и предоставляется читателю в качестве несложного самостоятельного упражнения.