Принадлежность точки к треугольнику (4 видео)

Точка внутри треугольника

Онлайн калькулятор определяет лежит ли точка внутри треугольника + показывает это наглядно на координатной плоскости.
Под калькулятором вы найдете способ определения принадлежности точки треугольнику.

Известны координаты вершин треугольника и известный координаты точки. Нужно установить принадлежность точки треугольнику.
Существует несколько способов определения. лежит-ли точка внутри треугольника или снаружи:

1. Метод сравнения площадей — по формуле Герона находятся площади 3-х треугольников которые образует точка с каждой стороной треугольника, далее находится площадь самого треугольника и сравнивается с суммой 3ех предыдущих треугольников, если суммы равны то значит точка принадлежит треугольнику.

2. Метод относительности — выбирается ориентация движения по вершинам треугольника, например по часовой стрелке. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Если точка для всех прямых, лежит с правой стороны, то значит точка принадлежит треугольнику, если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.

3. Метод геометрического луча — из точки пускается луч по какой-либо оси в каком-либо направлении. Вычисляется количество пересечений со сторонами, если кол-во нечётное, то значит точка лежит внутри многоугольника.

Содержание

Определение принадлежности точки треугольнику
Метод сравнения площадей
Метод относительности
Всё относительно!
Векторный метод
Как определить лежит ли точка внутри треугольника или снаружи.
Точка в треугольнике
Векторное произведение ( z — координата )
Точка внутри треугольника. Описание алгоритма.
📽️ Видео

Видео:Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать

Определение принадлежности точки треугольнику

Дано: у нас есть треугольник, нам известны только координаты его вершин. У нас есть точка, нам известны её координаты.

Что нужно узнать: нужно установить принадлежность точки треугольнику.

В данной статье разбирается несколько разных методов определения принадлежности точки треугольнику.

Видео:Задача о принадлежности точки многоугольникуСкачать

Метод сравнения площадей

В данном методе сначала находятся площади 3-х треугольников, которые образует данная точка с каждой стороной треугольника. В нашем случае(рис. 1) это треугольники ABP, BCP, CAP и их площади s1, s2, s3 соответственно.

Затем находится площадь самого треугольника ABC.

Найденный площади сравниваются — если сумма 3-х площадей равна площади всего треугольника, то значит точка принадлежит треугольнику. При сравнении, как правило, задаётся погрешность.

Так как у нас известны только координаты точек, то все площади, находятся по формуле Герона, от обильности операций которой становится ясно, почему этот метод очень трудоёмкий.

Простейшая реализация алгоритма:

Атрибуты функции: aAx, aAy, aBx, aBy, aCx, aCy — координаты точек A, B, C треугольника; aPx, aPy — координаты точки, принадлежность которой надо определить.

Видео:Алгоритмы. Попадание точки в треугольникСкачать

Метод относительности

Данный метод заключается в следующем. Сначала выбирается ориентация движения по вершинам треугольника(по часовой или против часовой стрелке). Я выбираю по часовой. На рисунке 2 выбранная ориентация движения(по часовой) показана стрелками. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Не трудно догадаться, что если точка для всех прямых, при нашей ориентации, лежит с правой стороны, то значит точка принадлежит треугольнику, а если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.

На рисунке 2 продемонстрирована ситуация, когда точка только для одной прямой AB лежит по левую сторону, а значит не принадлежит треугольнику.

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Всё относительно!

Тут надо кое что пояснить, весьма не маловажное, что может сыграть роль в оптимизации и выборе алгоритма. Обратите внимание, что в приведённом коде есть закомментированные блоки кода с комментариями «для строгой ориентации», в то время как рабочий код универсален — он предназначен для любой ориентации. Т.е. представленный код определит принадлежность точки для любого заданного треугольника. В моей тестирующей программе треугольники как раз таки строятся по random()-у координат вершин, а ориентация идёт по вершинам(A>B>C>A). Для рисунка 2 — это по часовой стрелки, но для рисунка 3 — это против часовой.

Так вот, в случае рисунка 3 точка должна лежать по левую сторону векторов, чтобы принадлежать треугольнику.

Вот тут и получается важный момент! Если вы уверены, что в вашем проекте все треугольники будут ориентированы по часовой стрелке(а т.е. вершина C будет всегда правее вектора AB), то вам можно закомментировать блок универсального решения и раскомментировать блок «для строгой ориентации по часовой» и данный алгоритм упрощается аж на 3 логических операции!

Видео:Построение треугольника, симметричного данному относительно точки, принадлежащей его сторонеСкачать

Векторный метод

Третий метод который я освещаю для меня самый интересный.

Идея его применения зарождается если взглянуть на треугольник как на половинку параллелограмма…

Данный метод я сначала проверил на бумаге. После всех оптимизаций формул, как всё сошлось, я реализовал его в коде, где он показал себя вполне успешным и результативным. Аж эффективнее 2-х предыдущих методов :]

1) одну вершину треугольника помещаем в координаты (0;0);

2) две стороны, выходящие из этой вершины, представляем как вектора.

Таким образом из всего этого появляется система простых условий нахождения точки P между векторами b и c.(рис. 4)

Рис. 4.

Видео:Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Как определить лежит ли точка внутри треугольника или снаружи.

Калькулятор поможет определить находится ли заданная точка внутри заданного треугольника. Точка и треугольник задаются декартовыми координатами на плоскости. Детально описан алгоритм вычисления.

Этот калькулятор определит где находится заданная точка внутри 2-мерного треугольника или вовне. Калькулятор использует простой алгоритм, основанный на свойствах векторного произведения. Описание этого алгоритма можно найти сразу за калькулятором.

Точка в треугольнике

Векторное произведение ( z — координата )

Видео:Принадлежность точки прямой, лучу, отрезкуСкачать

Точка внутри треугольника. Описание алгоритма.

Векторное произведение векторов a и b, заданного декартовыми координатами в пространстве для 3-х мерного правого ортонормального базиса можно выразить так:
[1].
Векторное произведение обладает свойством антикоммутативности:

Это важное свойство мы будем использовать для решения нашей задачи.

Попарное векторное произведение векторов-сторон треугольника и вектора из вершины в точку

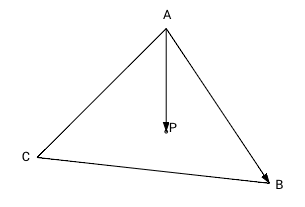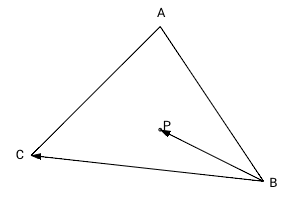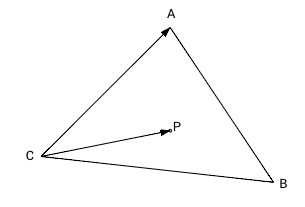
Для того чтобы определить лежит ли точка P внутри треугольника ABC мы вычислим 3 векторных произведения: ABxAP, BCxBP and CAxCP. Так как наш треугольник и точка в 2-мерном пространстве на плоскости, третья координата z для трехмерного пространства равна нулю. Согласно формуле [1] мы можем не вычислять координаты x и y для векторного произведения, если координата z векторов-множителей равна нулю — координаты x и y результата в этом случае всегда равны нулю (результирующий псевдо-вектор перпендикулярен плоскости треугольника). Знак результата произведения для оставшейся координаты (z) зависит от относительного положения умножаемых векторов. Если первый вектор (в нашем случае это сторона треугольника) находится правее второго вектора (вектор из вершины в точку P), то координата z результата будет положительна, если первый вектор будет левее второго — отрицательна, и в противном случае, если оба вектора идут в одном и том же направлении, результат будет равен нулю.
Получив результаты по трем векторным произведениям, нам остается их проанализировать, чтобы понять лежит ли точка внутри треугольника:
Если мы имеем и положительные и отрицательные результаты, точка лежит вне треугольника, если результаты только положительные или только отрицательные, точка — внутри.
Таблица далее иллюстрирует все возможные варианты результатов векторного произведения: