🎶 Музыка и математика: исследуем ритм, гармонию и структуру

Погружение в уникальное слияние музыки и математики раскрывает неожиданные аспекты искусства и науки. Музыкальная математика — это исследование, которое выявляет структуру и красоту музыки через математические концепции. Ритм, мелодия, и гармония музыки тесно связаны с числовыми отношениями, формулами и геометрическими фигурами, что делает эту область знания не только фасцинирующей, но и глубоко познавательной.

На заре цивилизации учёные и философы заметили, что музыкальные интервалы могут быть выражены через простые численные соотношения. Это открытие стало основой для развития музыкальной теории, где математика используется для анализа и создания музыкальных произведений. От ритмических паттернов, определяющих темп и ритм произведения, до сложных гармонических структур, лежащих в основе мелодии и аккордов — всё это подчиняется математическим законам.

Гармония, один из столпов музыкальной теории, также тесно связана с математикой. Она исследует, как различные звуки могут одновременно сочетаться, создавая приятные для слуха комбинации. Эти отношения могут быть описаны с помощью математических пропорций, отражающих золотое сечение и другие геометрические соотношения, найденные в природе и искусстве.

Разбор структуры музыкальных произведений с математической точки зрения выявляет повторяющиеся паттерны и фракталы, что не только обогащает восприятие музыки, но и предоставляет композиторам новые инструменты для творчества. Эта синергия музыки и математики демонстрирует, как через числа и формулы можно выразить эмоции и красоту, делая каждое музыкальное произведение уникальным исследованием человеческого опыта и восприятия.

Видео:Математика Музыки и ЗвуковСкачать

🔢 Ритм и его математическая природа: отсчет времени в музыке

Ритм в музыке – это порядок, вносящий ясность в поток звуков, определяя их длительность и последовательность во времени. Этот элемент музыки тесно связан с математическими концепциями, такими как метрика, счет и доля. Изучение ритмических структур раскрывает их основу на числовых отношениях, подчеркивая упорядоченность и предсказуемость музыкальных произведений.

Для осмысления ритма важно понять его строение. Музыкальные такты, разделенные на равные интервалы, формируют ритмическую сетку. Число ударов в такте и их распределение создают различные ритмические паттерны, что лежит в основе восприятия музыкального темпа и грува. Эти паттерны, повторяющиеся через равные промежутки времени, обеспечивают структуру и узнаваемость музыкальной композиции.

Математика ритма также проявляется в использовании долей и пропорций при создании музыкальных произведений. Сложение и деление ритмических единиц ведет к формированию комплексных и захватывающих ритмических структур. Использование синкоп, перерывов и акцентов в определенных точках такта дополнительно усиливает динамичность и выразительность музыки.

Внедрение ритмических образцов, основанных на математических последовательностях, например, в виде фибоначчиевой последовательности или других математических формул, придает композициям уникальность и глубину. Эти методы позволяют композиторам экспериментировать с темпом, создавая произведения, в которых ритм выступает не только как основа, но и как источник вдохновения.

Анализ ритма и его математические аспекты позволяют глубже понять структуру музыкальных композиций. Размышления о времени и его музыкальном измерении открывают новые горизонты для творчества и восприятия музыки. Погружение в мир ритмических закономерностей становится путешествием по пересечению искусства и науки, где каждое открытие ведет к новым возможностям и интерпретациям.

Видео:Откуда в МУЗЫКЕ так много МАТЕМАТИКИ?Скачать

📐 Гармония и пропорции: золотое сечение в музыкальных произведениях

Гармония в музыке — это не просто сочетание звуков, но и математическое искусство, где пропорции играют ключевую роль. Золотое сечение, известное своим присутствием в искусстве и природе, также находит свое отражение в музыкальных композициях.

Этот уникальный принцип пропорциональности можно обнаружить в структуре многих известных музыкальных произведений. Он определяет точки кульминации и переходы, создавая удивительное ощущение равновесия и эстетического удовлетворения.

Исследование влияния золотого сечения на музыку открывает новые горизонты для понимания того, как математика может влиять на наше восприятие искусства и красоты.

Видео:Как устроена музыкальная гармония. Пространство кратностей – математик Роман Олейников | НаучпопСкачать

🎼 Структура музыкальных композиций: формы и математические модели

Каждое музыкальное произведение – это уникальное сочетание мелодии, ритма и гармонии, объединенных в одну структуру. Эта структура не случайна; она следует определенным математическим моделям и формам, которые создают основу для музыкальной композиции. Основы этих структур уходят корнями в глубокую древность, когда композиторы начали применять численные отношения для создания музыкального баланса и красоты.

Музыкальные формы, такие как соната, фуга или канон, основываются на строгих математических принципах. Эти формы определяют, как развивается музыкальное произведение, указывая на повторение тем, модуляцию и развитие идей в рамках композиции. Например, форма сонаты включает в себя экспозицию, развитие и рекапитуляцию, каждая из которых имеет четкую структуру и функцию в общем контексте произведения.

Математические модели в музыке не ограничиваются только формами. Они также включают в себя серийную технику, алгоритмическую композицию и даже использование математических алгоритмов для создания музыки. Серийная техника, например, использует строгий порядок для организации музыкальных элементов, таких как высота тонов, динамика и ритм, обеспечивая композитору средства для структурирования музыки на основе численных отношений.

В современной музыке математические модели и компьютерные алгоритмы открывают новые горизонты для композиторов. Они позволяют экспериментировать с звуком и структурой, создавая произведения, которые были бы невозможны без использования этих технологий. От генеративной музыки до алгоритмической композиции, эти подходы размывают границы между музыкой и математикой, демонстрируя, как математические принципы могут быть использованы для создания новых музыкальных форм и звучаний.

Видео:Музыкальная математика за 13,5 минутСкачать

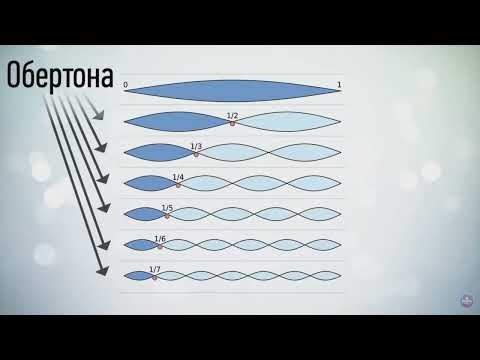
🔊 Частоты и интервалы: численное выражение музыкальных звуков

Частоты и интервалы являются основополагающими элементами музыкальной теории, представляя собой количественные характеристики звуков. Частота звука определяет его высоту, а интервалы — это различия в высоте между двумя звуками.

В музыке, каждый звук имеет определенную частоту вибрации, измеряемую в герцах (Гц). Эти вибрации создают волны, которые наше ухо воспринимает как различные ноты. Интервалы между этими нотами формируют мелодии и аккорды, которые мы идентифицируем и ценим.

Математика предоставляет инструменты для анализа и понимания этих музыкальных явлений, позволяя композиторам создавать гармоничные и эстетически приятные произведения.

Видео:Алгебра гармонии. Часть I. От физики звука к пифагорову строю / 22 векСкачать

🌐 Музыкальные масштабы и темперация: математика настройки инструментов

Основа любой музыкальной композиции скрывается в её масштабах и настройке, где математика играет ключевую роль. Масштабы определяются последовательностью звуков, которые формируют музыкальное пространство произведения. Точная настройка инструментов, основанная на математических расчётах, обеспечивает гармонию и чистоту звучания.

Темперация, система настройки, позволяет музыкантам исполнять произведения в различных тональностях без потери звуковой гармонии. Этот метод включает в себя небольшие отклонения от идеальных математических пропорций для достижения компромисса между разными тональностями. Так, равномерно темперированный масштаб, наиболее распространённый в современной музыке, делит октаву на двенадцать равных полутонов, что позволяет инструментам звучать гармонично в любой тональности.

Настройка инструментов с использованием математики не ограничивается только клавишными. Струнные, духовые, и даже ударные инструменты требуют точной настройки для достижения оптимального звучания. К примеру, расчёт длины струны для гитары или скрипки основывается на физических и математических принципах, гарантирующих точность звука на каждом ладу или позиции.

Изучение музыкальных масштабов и темперации раскрывает удивительный мир, где математика и музыка встречаются, демонстрируя, как точные расчёты могут привести к созданию красивых и гармоничных музыкальных произведений. Эта симбиоз обогащает понимание музыки, подчёркивая важность математики в искусстве настройки и создании музыкальных инструментов.

Видео:Как Пифагор придумал музыку | Математика в музыке – Роман Олейников | НаучпопСкачать

🎹 Математика и полифония: сложность в многоголосии

Полифония, одно из самых увлекательных явлений в музыке, представляет собой искусство сочетания нескольких независимых мелодических линий, которые вместе создают гармоничное целое. Этот метод композиции демонстрирует удивительную математическую точность в организации музыкального пространства, позволяя каждой линии сохранять свою уникальность при одновременном слиянии в общую структуру.

Основополагающим принципом полифонии является принцип независимости и взаимодействия голосов. Каждая мелодическая линия развивается согласно собственной логике, однако в контексте композиции все линии взаимодействуют, образуя сложные гармонические и ритмические отношения. Это требует от композитора глубоких знаний в области музыкальной теории и математики, чтобы управлять многоголосием таким образом, чтобы достигалось желаемое музыкальное воздействие.

Математические методы в полифонии проявляются в строгих правилах контрапункта, определяющих возможные и невозможные сочетания мелодических линий. Контрапункт, искусство плетения независимых мелодий в единую ткань, основывается на принципах, которые можно сравнить с математическими алгоритмами. Он предписывает, как мелодии могут двигаться относительно друг друга, создавая гармоническую богатость и предотвращая музыкальные конфликты.

Практика полифонии также включает в себя использование канона и фуги, форм, в которых строгое повторение мелодических фраз сочетается с изменением их контекста через транспозицию на разные интервалы. Это не только демонстрирует математическую основу композиционных техник, но и обеспечивает богатство музыкальных ощущений, исследуя возможности вариации и развития музыкальной идеи.

Изучение полифонии открывает новые горизонты в понимании музыки как искусства, управляемого как эмоциональными, так и интеллектуальными процессами. Способность видеть и анализировать музыкальные произведения с точки зрения их математической структуры углубляет восприятие и повышает оценку сложности и красоты музыкального искусства.

Видео:Где в музыке математика? Анна Виленская о секрете идеальной гармонии звуковСкачать

🧮 Алгоритмы и композиция: использование математики в современном сочинении музыки

Современное музыкальное творчество неразрывно связано с математикой, особенно когда речь заходит о создании сложных композиций. Алгоритмы, как математические процедуры, находят применение в процессе компоновки музыкальных произведений, обеспечивая новые способы генерации гармонии и ритма.

Использование алгоритмического подхода позволяет композиторам экспериментировать с необычными музыкальными структурами, создавая произведения, которые могут удивлять и вызывать новые эмоциональные реакции у слушателей.

Таким образом, математика открывает двери в мир бесконечных музыкальных возможностей, предоставляя инструменты для разработки уникальных звуковых пейзажей и мелодий.

Видео:Научный метод в музыке | Математика в музыке – Роман Олейников | НаучпопСкачать

💡 Музыкальная акустика: наука о звуке и его математическое изучение

Изучение музыкальной акустики раскрывает загадки звуков, которые окружают нас каждый день. Этот раздел науки обращает внимание на то, как звуковые волны взаимодействуют с различными средами, проникая в суть музыкальных тонов и гармонии. Музыкальная акустика использует математические принципы для анализа и понимания этих явлений, предоставляя нам ключ к глубинному восприятию музыки.

Одним из основных элементов музыкальной акустики является изучение частот звуковых волн. Каждый музыкальный звук характеризуется определенной частотой, которая определяет его высоту. Эти частоты не только формируют основу музыкальной гармонии, но и позволяют различать разные музыкальные инструменты и их звучание. Математический анализ частот помогает раскрыть структуру музыкальных произведений и глубже понять принципы создания гармоничного звука.

Другой важной аспект музыкальной акустики является резонанс. Это явление, при котором тело или система откликается на определенные частоты, может быть описано с помощью математических уравнений. Резонанс играет ключевую роль в создании музыкальных инструментов, так как он определяет, как звук усиливается и передается в окружающую среду. Понимание резонанса позволяет создавать инструменты с желаемыми звуковыми характеристиками и улучшать их звучание.

Музыкальная акустика также занимается изучением отражения и поглощения звука, что имеет огромное значение для акустического оформления концертных залов и студий звукозаписи. Математические модели помогают инженерам и архитекторам проектировать помещения с оптимальными акустическими свойствами, гарантируя чистоту и ясность звучания музыки.

В заключение, музыкальная акустика представляет собой мост между миром музыки и точными науками, открывая перед нами удивительные связи между математикой и искусством звуков. Через призму чисел и уравнений мы начинаем по-новому воспринимать музыку, обогащая наше понимание и восприятие этого искусства.

Видео:Связь музыки и математики Т В ЧерниговскаяСкачать

📈 Анализ и теория музыки: математический подход к музыкальной теории

Погружение в мир музыкальной теории с использованием математического анализа открывает новые горизонты для понимания структуры и гармонии композиций. Изучение взаимосвязи между математикой и музыкой начинается с абстрактных понятий, таких как частоты, интервалы и ритмы, и приводит к более глубокому осмыслению музыкальных произведений. Математический анализ в музыке включает в себя расчеты и моделирование, позволяя разработать теоретические основы для создания, интерпретации и анализа музыкальных произведений.

Один из ключевых аспектов этого подхода заключается в использовании математических моделей для изучения гармонии и полифонии. Эти модели помогают исследователям и композиторам видеть скрытые связи между различными частями музыкальной композиции, а также понимать, как различные элементы взаимодействуют для создания целостного музыкального впечатления. Математика также играет важную роль в разработке и анализе музыкальных масштабов и темперации, позволяя точно настраивать музыкальные инструменты для достижения желаемого звучания.

Современные технологии расширяют возможности математического анализа в музыке, включая использование программного обеспечения для создания музыки и цифровых аудио рабочих станций. Эти инструменты основаны на математических принципах для моделирования звуков и создания музыкальных эффектов, что дает композиторам и исполнителям беспрецедентные возможности для экспериментов с звуком.

Математический подход к анализу и теории музыки вносит вклад в наше понимание музыки как формы искусства, предоставляя инструменты для глубокого изучения и интерпретации музыкальных произведений. Он подчеркивает уникальное переплетение логики и креативности, которое лежит в основе как музыкального, так и математического творчества, раскрывая новые аспекты красоты и сложности музыки.

Видео:Математика это не ИсламСкачать

🎧 Цифровая музыка и синтезаторы: математика в электронной музыке

Цифровая музыка и синтезаторы представляют собой уникальное пересечение музыкального искусства и математической точности. Синтезаторы, используя математические алгоритмы, преобразуют электронные сигналы в звуки, позволяя музыкантам создавать широкий спектр тембров и мелодий.

Математика в электронной музыке выходит за рамки простого создания звуков; она позволяет манипулировать и сложно структурировать музыкальное пространство, открывая новые горизонты для экспериментов и инноваций.

Так, цифровая обработка звука становится не только техническим процессом, но и творческим актом, где математика служит ключом к неограниченным возможностям музыкального выражения.

Видео:Как устроена музыка. ЧАСТЬ I.Скачать

👩‍🔬 Исследования и эксперименты: математика в музыкотерапии

Музыкотерапия, сочетающая искусство и науку, обретает новое измерение благодаря математике. Подобный подход, подкрепленный численными исследованиями, раскрывает потенциал музыки в лечебных и реабилитационных целях. В этом контексте математический анализ позволяет глубже понять структуры и паттерны, на которых основана музыка, и как они влияют на человеческий мозг и его функции.

Математика применяется для анализа ритмических структур и их воздействия на психологическое состояние человека. Через изучение частотных характеристик звуков и интервалов между ними ученые определяют, какие музыкальные композиции могут способствовать снижению стресса, улучшению концентрации или стимуляции когнитивных функций.

Одним из направлений является использование алгоритмов для создания музыкальных композиций, нацеленных на конкретные терапевтические эффекты. Это включает в себя разработку программного обеспечения, способного адаптироваться к индивидуальным нуждам слушателей, учитывая их предпочтения и специфические заболевания.

Исследования в области музыкотерапии также охватывают анализ влияния музыки на физиологические процессы, включая сердечный ритм и давление, что помогает создавать музыкальные произведения, способные оказывать непосредственное воздействие на тело человека.

Фрактальная теория музыки, изучающая повторяющиеся паттерны на различных уровнях музыкальной структуры, находит применение в музыкотерапии для создания композиций, которые могут индуцировать релаксацию и медитативные состояния. Это открывает новые горизонты для использования музыки в качестве терапевтического инструмента.

Комбинируя традиционные методы музыкотерапии с математическими моделями, исследователи и практикующие врачи разрабатывают инновационные подходы к лечению и реабилитации. Это позволяет не только расширить понимание механизмов воздействия музыки на человека, но и улучшить качество и эффективность музыкотерапевтических вмешательств.

Видео:Как устроена музыка. Логика гармонии музыки.Скачать

🔄 Паттерны и повторения: фракталы в музыке

Мир музыки богат повторяющимися мотивами и структурами, напоминающими фракталы — сложные геометрические фигуры, каждая часть которых является уменьшенной копией целого. Эти повторяющиеся элементы не просто украшают музыкальные произведения, но и создают их глубинную структуру, делая музыку одновременно предсказуемой и удивительно разнообразной.

Принцип фракталов в музыке выражается через самоподобие музыкальных фраз в разных масштабах композиции. Примером могут служить музыкальные произведения, в которых одна и та же мелодическая линия повторяется в различных тональностях или темпах, создавая сложную, но гармоничную структуру. Это не только техника композиции, но и способ восприятия музыки, когда слушатель улавливает повторения и различия, внося свой вклад в интерпретацию произведения.

Фрактальные структуры в музыке также находят отражение в ритмических паттернах. Ритмические фигуры, повторяющиеся на разных уровнях временной иерархии, создают сложные, но узнаваемые текстуры. Это явление можно наблюдать во многих традиционных и современных музыкальных стилях, где повторение и изменение ритмических мотивов формирует основу композиции.

Интерес к фракталам в музыке выходит за рамки теоретического анализа и становится источником вдохновения для композиторов. Использование фрактальных принципов позволяет создавать произведения, которые поражают своей красотой и сложностью, открывая новые горизонты для музыкального творчества. Эти паттерны и повторения, основанные на математических принципах, подчеркивают универсальность музыки как языка, который может быть одновременно исследован, понят и оценен на самых разных уровнях.

Таким образом, фракталы в музыке представляют собой уникальное переплетение науки и искусства, демонстрируя, как математические концепции могут обогащать музыкальное искусство, делая его более глубоким и многогранным. Это направление открывает новые перспективы для изучения и творчества, подчеркивая взаимосвязь между природой, математикой и культурой.

Видео:МУЗЫКА, МАТЕМАТИКА и РИТМ.Скачать

🌌 Влияние музыки на математическое мышление и наоборот

Музыка и математика — две стороны одной медали, взаимно обогащающие друг друга. Музыкальные произведения часто строятся на математических принципах, в то время как математическое мышление может быть улучшено благодаря музыкальной практике.

Изучение музыки способствует развитию абстрактного мышления, улучшает память и внимание, что положительно сказывается на математических способностях. С другой стороны, математика предоставляет инструменты для анализа музыкальных композиций, раскрывая их внутреннюю структуру и закономерности.

Таким образом, музыка и математика взаимодействуют, создавая гармоничное сочетание логики и творчества, что приводит к новым открытиям и инновациям в обеих областях.

💡 Видео

Великое в малом. Музыка и математикаСкачать

Математика в музыкеСкачать

Музыка - искусство или математика? / Утренний эфирСкачать

Мини-лекция учителя музыки А.В. Зарубы "Математика - музыка... Музыка - математика..."Скачать

Математические методы в музыкеСкачать

Музыка 5. Ритм и метр в музыке. Метроном и темп. Ритм-секция — Академия занимательных наукСкачать

Пушной — математика и музыка на флексе!Скачать