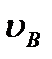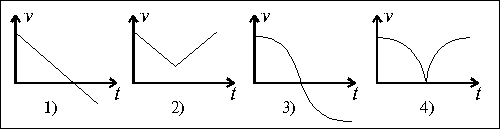При равнозамедленном движении точки по окружности по часовой стрелке

Дата добавления: 2015-08-31 ; просмотров: 13808 ; Нарушение авторских прав

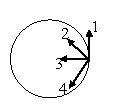
1.При равнозамедленном движении материальной точки по окружности по часовой стрелке вектор ее полного ускорения имеет направление, указанное на рисунке цифрой…

Варианты ответа: 3 4 2 1

2. Материальная точка M движется по окружности со скоростью v. На рис.1 показан график зависимости проекции скорости V_t от времени ( t– единичный вектор положительного направления, V_t – проекция на это направление). При этом вектор полного ускорения на рис.2 имеет направление …

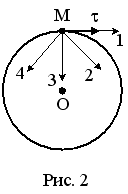
Варианты ответа: 2 3 1 4

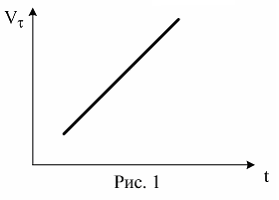
3.Материальная точка M движется по окружности со скоростью v. На рис.1 показан график зависимости проекции скорости V_t от времени ( t– единичный вектор положительного направления, V_t – проекция на это направление). При этом для нормального а_n и тангенциального а_t ускорения выполняются условия…

Варианты ответа:

4.Материальная точка M движется по окружности со скоростью v. На рис.1 показан график зависимости проекции скорости V_t от времени ( t– единичный вектор положительного направления, V_t – проекция на это направление). При этом для нормального а_n и тангенциального а_t ускорения выполняются условия…

Варианты ответа:

5.Материальная точка M движется по окружности со скоростью v. На рис.1 показан график зависимости проекции скорости V_t от времени ( t– единичный вектор положительного направления, V_t – проекция на это направление). При этом для нормального а_n и тангенциального а_t ускорения выполняются условия…

Варианты ответа:

6. Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина полного ускорения…

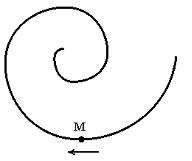
Варианты ответа: не изменяется увеличивается уменьшается

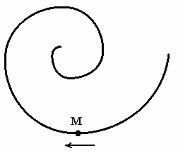
7. Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения …
Варианты ответа:

не изменяется увеличивается уменьшается

8. Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина полного ускорения…

Варианты ответа: не изменяется увеличивается уменьшается

9. Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости…

Варианты ответа:

не изменяется увеличивается уменьшается

10.Тело движется по траектории, указанной на рисунке, так, что его нормальное ускорение остается постоянным. В какой точке траектории скорость тела наибольшая?

Варианты ответа : а. Q б. K в. L

11. Тело движется по траектории, указанной на рисунке, так, что его скорость остается постоянной. В какой точке траектории нормальное ускорение тела наименьшее?

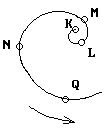
Варианты ответа:

а. K; б. L; в. M; г. N; д. Q.

12.При каком из приведенных ниже движений нормальное ускорение равно нулю?

Варианты ответа:

а. при гармонических колебаниях.

б. при криволинейном движении.

в. При равномерном движении по окружности.

г. При всех перечисленных видах движения.

д. При прямолинейном движении.

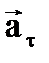
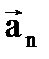
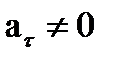
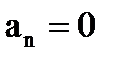
13.Если и – тангенциальная и нормальная составляющие ускорения, то соотношения: и справедливы для…

Варианты ответа:

а. прямолинейного равномерного движения;

б. прямолинейного равноускоренного движения;

в. равномерного движения по окружности;

г. неравномерного криволинейного движения

14.Если a_t и a_n – тангенциальная и нормальная составляющие ускорения, то соотношения: a_t=0, a_n =0 справедливы для…

Варианты ответа:

равномерного движения по окружности

равномерного криволинейного движения

прямолинейного равноускоренного движения

прямолинейного равномерного движения

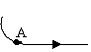
15. Тело движется с постоянной по величине скоростью по дуге окружности, переходящей в прямую, как показано на рисунке. Величина полного ускорения тела до точки А.

Варианты ответа:

постоянна, потом уменьшается до нуля

увеличивается, потом уменьшается до нуля

уменьшается, потом увеличивается

увеличивается, потом остается постоянной

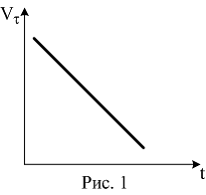
16.Тело движется с постоянной по величине скоростью по траектории, изображенной на рисунке. Для величины полного ускорения тела в точке А а_А и величины полного ускорения тела в точке В а_В справедливо соотношение…

Варианты ответа:

а_{А =} а_В =0

а_А

₂

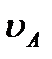
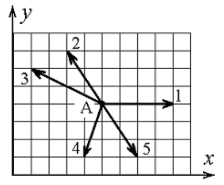
22.Радиус-вектор частицы изменяется во времени по закону r w:top=»1134″ w:right=»850″ w:bottom=»1134″ w:left=»1701″ w:header=»720″ w:footer=»720″ w:gutter=»0″/> «> 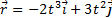. В момент времени 1 с частица оказалась в т.А. Ускорение частицы в этот момент времени имеет направление…

Варианты ответа: а. 1 б. 2 в. 3 г. 4 д. 5

23. Радиус-вектор частицы изменяется во времени по закону . В момент времени 1 с частица оказалась в т.А. Ускорение частицы в этот момент времени имеет направление…

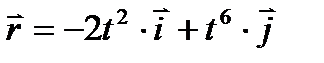
Варианты ответа: а. 1 б. 2 в. 3 г. 4 д. 5

24. На рисунке представлен график зависимости координаты от времени для тела, совершающего равнопеременное движение на некоторой планете. Определить начальную скорость этого тела.

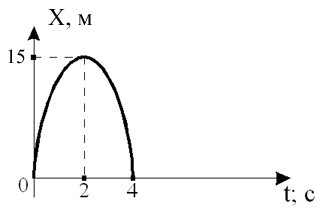
Варианты ответа:

а. 300 м/с б. 10 м/с в. 5 м/с г. 15 м/с д. 17.3 м/с

25.Линейная скорость материальной точки меняется со временем по закону V = 2t (м/с). Какой путь прошла точка за 1 секунду?

Варианты ответа: а. 1 м б. 0,5 м в. 1,5 м г. 2 м д. 2,5 м

26.Движение точки вдоль оси x задано уравнением x= 12 t – 2t 2 . Средняя скорость движения точки в интервале времени от 1 до 4 секунд равна…

а. 4 м /с б. 6 м/с в. 0,5 м /с г. 2 м /с

27.Для тела, брошенного вертикально вверх, проекция скорости тела на вертикальную ось, направленную вверх, будет изменяться в соответствии с графиком:

а. 1 б. 2 в. 3 г. 4

28. Тангенциальное ускорение точки меняется согласно графику. Такому движению соответствует зависимость скорости от времени…

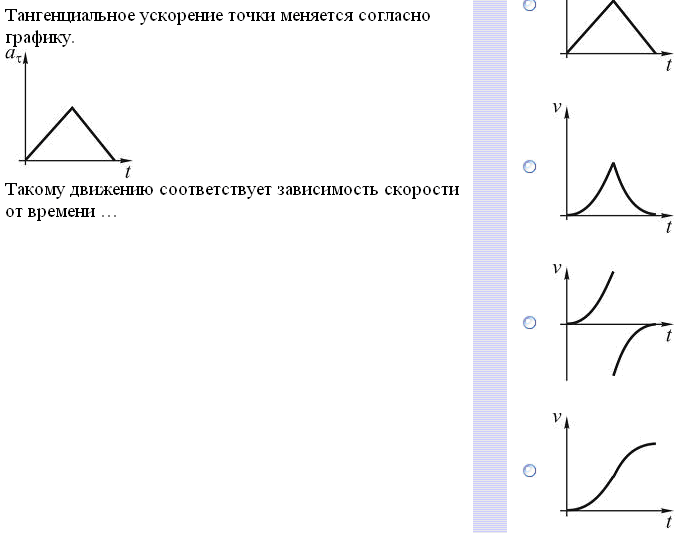
29.Тангенциальное ускорение точки меняется согласно графику. Такому движению соответствует зависимость скорости от времени…

Не нашли то, что искали? Google вам в помощь!

Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Виды движения по окружности

Угловое движение можно условно разделить на два вида:

1. Когда изменяется только направление вектора линейной скорости, а его длина не изменяется.
2. Или, когда изменяются обе характеристики вектора линейной скорости.

Во втором случае, для описания движения будем применять более сложные формулы кинематики. Так как появится еще один вид ускорения.

Центростремительное (нормальное) ускорение есть всегда, когда есть движение по окружности, при этом не важно, меняется ли скорость тела по модулю, или не меняется.

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Движение по окружности с постоянной по модулю скоростью

Пусть тело движется по окружности, но при этом длина вектора линейной скорости не меняется (рис. 1).

[left|vec right| = const]

На рисунке 1 указаны: а) – вид сбоку, б) вид сверху, вектор угловой скорости направлен к нам перпендикулярно рисунку.

Скорость будет меняться только по направлению от точки к точке, потому, что на тело действует центростремительная сила (displaystyle vec<F_<text>>) , тело обладает центростремительным (displaystyle vec<a_<text>>) (нормальным) ускорением.

Кроме линейной, тело обладает угловой скоростью. Если линейная скорость не изменяется по модулю, то длина вектора угловой скорости не меняется.

На рисунке 1а изображен вектор угловой скорости (displaystyle vec), на рисунке 1б вектор угловой скорости направлен к нам перпендикулярно плоскости рисунка. Направление, в котором тело движется по окружности, указано синей стрелкой.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Тангенциальное ускорение – когда модуль скорости меняется

Тело может увеличивать или уменьшать свою скорость, когда движется по окружности.

В таком случае, дополнительно к нормальному ускорению возникает тангенциальное (displaystyle vec<a_>) ускорение.

Тангенциальное ускорение играет роль линейного ускорения при прямолинейном движении тела. Вектор (displaystyle vec<a_>) направлен параллельно вектору (displaystyle vec) скорости.

Подобно движению по прямой, вектор ускорения – это первая производная скорости по времени, или вторая производная перемещения по времени.

Когда векторы скорости (vec) и ускорения (vec<a_>) сонаправлены (рис. 2), линейная и угловая скорости возрастают.

А когда ускорение (vec<a_>) направлено противоположно (рис. 3) вектору скорости (vec), угловая и линейная скорости уменьшаются.

С линейной скоростью (vec) связана угловая (vec) скорость.

Из рисунков 2, 3 следует: когда появляется тангенциальное ускорение, меняется и угловая скорость. Значит, тангенциальное ускорение (vec<a_>) появляется совместно с угловым (vec) ускорением и между ними есть связь.

Связь между тангенциальным и угловым ускорением выглядит аналогично связи между линейной и угловой скоростью.

В векторном виде

В скалярном виде

[ large boxed < a_= beta cdot R >]

(displaystyle vec left( frac<text><c^>right)) – угловое ускорение;

(displaystyle vec< a_> left( frac<text><c^>right)) – тангенциальное ускорение;

(R left( textright)) – радиус окружности.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Равноускоренное движение по окружности

Угловая скорость увеличивается (рис. 2), когда угловое ускорение сонаправлено с вектором угловой скорости. Когда движение происходит с постоянным ускорением, его называют равноускоренным.

Для решения задач на равноускоренное движение по окружности, поступаем аналогично равноускоренному движению по прямой. Применяем систему из двух уравнений:

[ large boxed < beginomega = omega _ + beta cdot t \ displaystyle varphi = omega_ cdot t + beta cdot frac end > ]

Первое уравнение системы – это связь между начальной (omega_ ) и конечной (omega ) скоростью. Второе уравнение – это уравнение движения.

Видео:Ускорение при равномерном движении по окружностиСкачать

Равнозамедленное движение по окружности

Когда векторы (vec) и (vec) направлены в противоположные стороны, угловая скорость (vec) уменьшается (рис. 3).

Для решения задач кинематики, в которых угловая скорость уменьшается и, движение равнозамедленное, используем систему, состоящую из таких уравнений:

[ large boxed < beginomega = omega _ — beta cdot t \ displaystyle varphi = omega_ cdot t — beta cdot frac end > ]

Видео:Физика - движение по окружностиСкачать

Общее ускорение при движении по окружности

Пусть точка движется по окружности и линейная (vec) скорость ее изменяется по модулю. При этом, точка обладает двумя видами ускорения — нормальным и тангенциальным. Эти виды ускорения обозначают символом (vec).

Примечание: Любое ускорение, обозначаемое символом «a», измеряется в метрах, деленных на секунду в квадрате.

Направление вектора общего ускорения указано на рисунке 4а, а для равнозамедленного – на рисунке 4б.

Так как векторы (vec<a_>) и (vec<a_>) всегда перпендикулярны, длину вектора общего ускорения (vec) можно найти из теоремы Пифагора:

Видео:Центростремительное ускорение. 9 класс.Скачать

I. Механика

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Видео:Лекция 6.1 | Описание движения по окружности | Александр Чирцов | ЛекториумСкачать

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Видео:Физика 10 Равномерное движение точки по окружностиСкачать

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Видео:#3.1 Движение по окружности. Центростремительное ускорение.Скачать

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Видео:РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Видео:Физика | Равномерное движение по окружностиСкачать

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

🔥 Видео

Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать