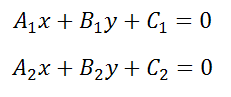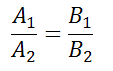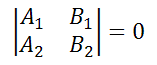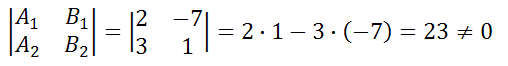Необходимым и достаточным условием параллельности двух прямых, заданных уравнением:
служит равенство их угловых коэффициентов, то есть
Если прямые заданы уравнениями в общем виде, то есть
то условие параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны:
или в другом представлении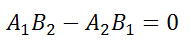 
Также это равенство можно записать в виде
Если свободные члены пропорциональны, то есть,
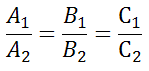
то прямые не только параллельны, но и совпадают.
4x+2y-8=0 и 8x+4y-16=0
представляют одну и ту же прямую, то есть совпадают.
Пример 2
Прямые у=4x-3 ( на графике синего цвета ) и y=4x+7 ( прямая красного цвета ) параллельны, так как у них угловые коэффициенты равны k1=k2=4
Пример 3
Прямые у=5x+1 и y=3x-4 не параллельны, так как у них угловые коэффициенты не равны, т.е. k1=5, k2=3
Пример 4
Прямые 2x+4y+7=0 и 3x+6y-5=0 параллельны, так как выражение равно нулю
Пример 5
Прямые 2x-7y+7=0 и 3x+y-5=0 не параллельны, так как выражение не равно нулю
Видео:Алгебра 7 класс. При каком значении k график функции y = kx - 2 проходит через точку А(15; -7)Скачать
при каких значениях k прямые kx+3y+5=0 и (k+1)x-2y-1=0 параллельны
Преобразуем
у=-(к/3)х-5/3
у=((к+1)/2)х-1/2
Прямые параллельны, если -к/3=(к+1)/2
-2к=3к+3
к=-3/5
Когда нормальные векторы (k;3) и (k+1;-2) коллинеарны.
k/(k+1)=-3/2
2k=-3k-3
5k=-3
k=-3/5
Варианты ответов:
1) -3 и 2
2) -3/5
3) -3 и 5
4) 3/5
5) -5 и 3
Видео:При каких значениях параметра c прямая y=c имеет с графиком ровно одну общую точку.Скачать
Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Расстояние от точки до прямой на плоскости
ПРЯМАЯ НА ПЛОСКОСТИ
Взаимное расположение прямых на плоскости. Угол между прямыми на плоскости. Расстояние от точки до прямой на плоскости
Показать, при каких условиях прямые на плоскости параллельны, пересекаются, совпадают. Рассмотреть случаи, когда прямые заданы каноническими, общими или уравнениями с угловым коэффициентом. Научить находить косинус угла между пересекающимися прямыми и координаты точки их пересечения. Научить находить расстояние от точки до прямой на плоскости и расстояние между параллельными прямыми.
1) Школьники должны знать:
− условия, при которых прямые пересекаются, параллельны, совпадают, в случаях, если прямые заданы общими уравнениями, каноническими, уравнениями с угловым коэффициентом;
− условия, при которых прямые перпендикулярны;
− формулу для нахождения расстояния от точки до прямой на плоскости;
− формулу для нахождения косинуса угла между пересекающимися прямыми в случаях, если прямые заданы общими уравнениями, каноническими, уравнениями с угловым коэффициентом.
2) Школьники должны уметь:
− выяснять взаимное расположение прямых на плоскости;
− находить угол между прямыми на плоскости;
− находить расстояние от точки до прямой на плоскости;
− находить расстояние между параллельными прямыми на плоскости.
Взаимное расположение прямых на плоскости
Прямые на плоскости могут совпадать, пересекаться или быть параллельными.
1.Пусть на плоскости заданы общими уравнениями две прямые L1 и L2:
где 
и 
– нормальные векторы прямых L1 и L2, соответственно.
а) совпадают, если
− нормальные векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, лежит также и на второй прямой
.
б) параллельны, если
− нормальные векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, не лежит на второй прямой.
.
в) пересекаются, если нормальные векторы прямых не коллинеарны, а значит, их координаты не пропорциональны, т. е.
.
2.Пусть на плоскости заданы прямые L1 и L2 каноническими уравнениями:
а) совпадают, если
− направляющие векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, лежит также и на второй прямой
и 
.
б) параллельны, если
− направляющие векторы прямых коллинеарны, а значит, их координаты пропорциональны;
− точка, лежащая на первой прямой, не лежит на второй прямой.
и 
.
в) пересекаются, если направляющие векторы прямых не коллинеарны, а значит, их координаты не пропорциональны, т. е.
3.Если прямые L1 и L2 заданы уравнениями с угловым коэффициентом
а) совпадают, если k1 = k2 и b1 = b2;
б) параллельны, если k1 = k2 и b1 ¹ b2;
в) пересекаются, если k1 ¹ k2.
Угол между прямыми на плоскости
Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.
1.Пусть на плоскости заданы прямые L1 и L2 общими уравнениями:
Тогда косинус наименьшего угла между прямыми L1 и L2 на плоскости равен модулю косинуса угла между нормальными векторами этих прямых:
В случае если прямые L1 и L2 перпендикулярны, их нормальные векторы также перпендикулярны, а значит, скалярное произведение нормальных векторов должно быть равно нулю, т. е. 
.
2.Пусть прямые L1 и L2 заданы каноническими уравнениями:
Тогда косинус наименьшего угла между прямыми L1 и L2 равен модулю косинуса угла между направляющими векторами этих прямых:
2. Пусть прямые L1 и L2 заданы уравнениями с угловым коэффициентом
Тогда тангенс наименьшего угла между прямыми L1 и L2 можно найти по формуле:
,
где k1 и k2 – угловые коэффициенты прямых L1 и L2.
Очевидно, что две прямые будут параллельны, если их угловые коэффициенты будут равны.
Итак, условие параллельности двух прямых:
Если две прямые перпендикулярны, т. е. угол φ = p/2, мы получим
Это будет иметь место, когда
Итак, условие перпендикулярности двух прямых:
Расстояние от точки до прямой на плоскости
Расстояние от точки до прямой, не содержащей эту точку, есть длина перпендикуляра, проведенного из этой точки на прямую.
Расстояние от точки до прямой можно вычислить:
1) Как длину отрезка перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот;
2) Используя координатно – векторный метод.
Пусть на плоскости заданы прямая L и точка M, не принадлежащая этой прямой
–
расстояние от точки М0(x0, y0) до прямой L.
Замечание. Расстояние между двумя параллельными прямыми на плоскости можно найти по последней формуле, если находить расстояние от любой точки, принадлежащей одной прямой, до другой прямой.
Даны координаты точек A(4, 1), B(2, −1), C(−3, 5). Найти угол между медианой и высотой, проведенными из вершины A.
Напишем уравнение высоты AH. Для любой точки M(x, y), лежащей на прямой AH, вектор 
перпендикулярен вектору 
, а значит, скалярное произведение этих векторов должно быть равно нулю, т. е. 
.
и 
,
Итак, уравнение высоты AH:
Напишем уравнение медианы, проведенной из вершины A. Найдем координаты точки D. Точка D − середина отрезка BC, значит, ее координаты можно найти как среднее арифметическое координат точек B и C. Координаты точек B(2, −1) и C(−3, 5), тогда координаты точки D:
Для любой точки N(x, y), лежащей на медиане AD, вектор 
коллинеарен вектору 
, а значит, координаты этих векторов должны быть пропорциональны. Найдем координаты векторов и :
Запишем условие пропорциональности координат:
(умножим на (1/2));
По свойству пропорций получим:
.
Получили общее уравнение медианы AD:
.
Косинус наименьшего угла между прямыми равен модулю косинуса угла между нормальными векторами этих прямых.
Уравнение прямой AH: Тогда нормальный вектор этой прямой − 
. Уравнение прямой AD: . Тогда нормальный вектор этой прямой − 
.
.
Ответ: 
.
Даны координаты точек A(4, 1), B(2, −1), C(−3, 5). Найти расстояние от точки A до прямой BC.
Напишем уравнение прямой BC. Для любой точки N(x, y), лежащей на прямой BC, вектор 
коллинеарен вектору 
, а значит, координаты этих векторов должны быть пропорциональны:
.
Перемножив по свойству пропорций, перейдем к общему уравнению прямой:
Тогда общее уравнение прямой BC:
.
Точка A(4, 1) 
BC. Расстояние от точки до прямой на плоскости можно найти по формуле:
где 
.
.
Ответ: расстояние от точки A до прямой BC равно 
.
Выяснить взаимное расположение прямых L1 и L2. Если прямые пересекаются, то найти угол между ними и координаты точки их пересечения, а если параллельны, то найти расстояние между ними:
L1: 
;
L2: 
;
Запишем координаты нормальных векторов прямых L1 и L2:
L1: , тогда 
– нормальный вектор прямой L1;
L2: , тогда 
– нормальный вектор прямой L2.
Найдем отношение координат нормальных векторов прямых:
.
Так как координаты нормальных векторов пропорциональны, то векторы 
и 
коллинеарны, а значит, прямые L1, и L2 либо параллельны, либо совпадают.
Прямые параллельны так как
.
Расстояние между прямыми найдем, как расстояние от точки М1, лежащей на прямой L1, до прямой L2 по формуле:
где 
.
Найдем координаты точки M1, принадлежащей прямой L1. Для этого одну из координат, например y0, примем равной нулю, тогда x0 = 4, значит, точка 
.
Ответ: прямые параллельны, расстояние между ними равно 
.
Выяснить взаимное расположение прямых L1 и L2. Если прямые пересекаются, то найти угол между ними и координаты точки их пересечения, а если параллельны, то найти расстояние между ними:
Найдем направляющие векторы прямых L1 и L2:
,
то координаты направляющих векторов не пропорциональны. Следовательно, прямые L1 и L2 пересекаются.
Косинус наименьшего угла между прямыми равен модулю косинуса угла между направляющими векторами этих прямых.
Найдем координаты точки пересечения прямых L1 и L2. Для этого получим общие уравнения этих прямых.
Пусть точка М (x0, y0) − точка пересечения прямых L1 и L2. Тогда координаты точки М должны удовлетворять обоим уравнениям. Решим систему уравнений:
Следовательно, точка 
− точка пересечения прямых L1 и L2.
Ответ: прямые пересекаются, 
, точка пересечения прямых − точка .
Задачи для усвоения пройденного материала.
1. Найти расстояние от точки А(−4, 1) до прямой, проходящей через точки B(1, −1), C(1, 5).
2. Выяснить взаимное расположение прямых 
и 
.
3. Найти точку пересечения медиан треугольника, вершинами которого являются точки 
4. Найти точку пересечения высот треугольника, вершинами которого являются точки
5. Написать уравнение прямой, проходящей через точку 
и составляющей угол 450 с прямой 
.
6. Найти угол между прямыми 
и
1. При каких значениях параметров прямые 
и 
параллельны? совпадают? пересекаются?
2. При каких значениях параметров прямые 
и 
параллельны? совпадают? пересекаются?
3. При каких значениях параметров прямые 
и 
параллельны? совпадают? пересекаются?
4. Как найти угол между пересекающимися прямыми,?
5. Как найти координаты точки пересечения прямых?
6. Как найти расстояние между параллельными прямыми?
7. При каких значениях параметров прямые 
и 
параллельны? совпадают? пересекаются?
🎬 Видео
Параллельные прямые | Математика | TutorOnlineСкачать
Прямая в пространстве. Лекция.Скачать
ЗАДАНИЕ 22. ПОСТРОИТЬ ГРАФИК ФУНКЦИИ. НАХОДИМ КОЭФФИЦИЕНТ К. ОГЭ 2021Скачать
Мокроусов И.С. | Лекция 18 по Алгебре и геометрии | ВМК МГУСкачать
6. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ НЕ ИМЕЕТ КОРНЕЙСкачать
Перпендикулярные прямые. 6 класс.Скачать
14.05.2024 Двадцатая лекция по линейной алгебре и геометрии (квадрики)Скачать
Разбор досрока, математика, ЕГЭ 2023, 13, 16, 18 заданияСкачать
Мокроусов И.С. | Семинар N+3 по Алгебре и геометрии | ВМК МГУСкачать
Параллельные прямые. 6 класс.Скачать
Линейная функция График Свойства Ч2 |Математика ЗнатикаСкачать
Алгебра и геометрия 6. Прямые и плоскость. Плоскость в пространствеСкачать
Линейная алгебра с элементами аналитической геометрии. Лекция 3Скачать
АиСД, лекция 26:вычислительная геометрияСкачать
Прямые m и n параллельны. Найдите ∠3, если ∠1=24°, ∠2=90° | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать
Геометрия, 11 класс ЕМН, СОЧ за II четвертьСкачать
Высшая математика лекция 8Скачать
Алгебра и геометрия. Лекция 7. Прямая в пространстве. Алгебраические кривые в пространствеСкачать
