In this post, we will learn how to detect lines and circles in an image, with the help of a technique called Hough transform.
- What is Hough transform?
- Hough transform to detect lines in an image
- Equation of a line in polar coordinates
- Accumulator
- Step 1 : Initialize Accumulator
- Step 2: Detect Edges
- Step 3: Voting by Edge Pixels
- HoughLine: How to Detect Lines using OpenCV
- Line Detection Result
- HoughCircles : Detect circles in an image with OpenCV
- Circle Detection Result
- Subscribe & Download Code
- Обнаружение кругов с использованием OpenCV | питон
- Преобразование хафа для поиска окружностей python
- 🔥 Видео
Видео:Распознавание объектов на Python | Поиск объектов на изображении | TensorFlow, PixelLibСкачать

What is Hough transform?
Hough transform is a feature extraction method for detecting simple shapes such as circles, lines etc in an image.
A “simple” shape is one that can be represented by only a few parameters. For example, a line can be represented by two parameters (slope, intercept) and a circle has three parameters — the coordinates of the center and the radius (x, y, r). Hough transform does an excellent job in finding such shapes in an image.
The main advantage of using the Hough transform is that it is insensitive to occlusion.
Let’s see how Hough transform works by way of an example.
Видео:[Python] Введение в распознавание контуров через OpenCVСкачать
![[Python] Введение в распознавание контуров через OpenCV](https://i.ytimg.com/vi/oDCqxgc2wog/0.jpg)
Hough transform to detect lines in an image
Equation of a line in polar coordinates
From high school math class we know the polar form of a line is represented as:
(1)
Here 
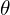
You may be tempted to ask why we did not use the familiar equation of the line given below
The reason is that the slope, m, can take values between – 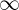
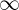
You may also have a follow-up question. In the 
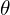

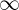

Accumulator
When we say that a line in 2D space is parameterized by 
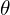

Imagine a 2D array where the x-axis has all possible 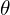

This 2D array is called an accumulator because we will use the bins of this array to collect evidence about which lines exist in the image. The top left cell corresponds to a (-R, 0) and the bottom right corresponds to (R, 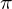
We will see in a moment that the value inside the bin (
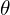

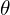
The following steps are performed to detect lines in an image.
Step 1 : Initialize Accumulator
First, we need to create an accumulator array. The number of cells you choose to have is a design decision. Let’s say you chose a 10×10 accumulator. It means that 
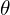
Step 2: Detect Edges
Now that we have set up the accumulator, we want to collect evidence for every cell of the accumulator because every cell of the accumulator corresponds to one line.
How do we collect evidence?
The idea is that if there is a visible line in the image, an edge detector should fire at the boundaries of the line. These edge pixels provide evidence for the presence of a line.
The output of edge detection is an array of edge pixels
Step 3: Voting by Edge Pixels
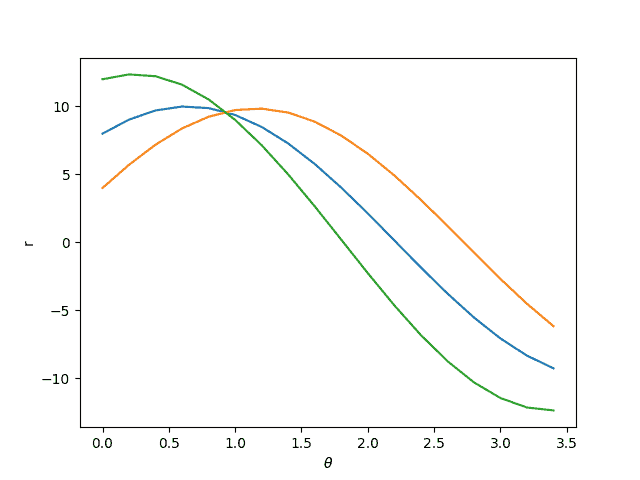
For every edge pixel (x, y) in the above array, we vary the values of 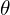
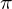

In the Figure below we vary the 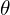

As you can see, these curves intersect at a point indicating that a line with parameters 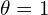
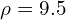
Typically, we have hundreds of edge pixels and the accumulator is used to find the intersection of all the curves generated by the edge pixels.
Let’s see how this is done.
Let’s say our accumulator is 20×20 in size. So, there are 20 distinct values of 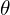

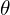

We do this for every edge pixel and now we have an accumulator that has all the evidence about all possible lines in the image.
We can simply select the bins in the accumulator above a certain threshold to find the lines in the image. If the threshold is higher, you will find fewer strong lines, and if it is lower, you will find a large number of lines including some weak ones.
Видео:Урок #3 Python / Распознавание контуров OpenCVСкачать

HoughLine: How to Detect Lines using OpenCV
In OpenCV, line detection using Hough Transform is implemented in the function HoughLines and HoughLinesP [Probabilistic Hough Transform]. This function takes the following arguments:
- edges: Output of the edge detector.
- lines: A vector to store the coordinates of the start and end of the line.
- rho: The resolution parameter
in pixels.
- theta: The resolution of the parameter
in radians.
- threshold: The minimum number of intersecting points to detect a line.
Download Code To easily follow along this tutorial, please download code by clicking on the button below. It’s FREE!
Python:
C++:
Line Detection Result
Below we show a result of using hough transform for line detection. Bear in mind the quality of detected lines depends heavily on the quality of the edge map. Therefore, in the real world Hough transform is used when you can control the environment and therefore obtain consistent edge maps or when you can train an edge detector for the specific kind of edges you are looking for.

HoughCircles : Detect circles in an image with OpenCV
In the case of line Hough transform, we required two parameters, (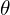

coordinates of the center of the circle.
- radius.
As you can imagine, a circle detector will require a 3D accumulator — one for each parameter.
The equation of a circle is given by
(2)
The following steps are followed to detect circles in an image: –
- Find the edges in the given image with the help of edge detectors (Canny).
- For detecting circles in an image, we set a threshold for the maximum and minimum value of the radius.
- Evidence is collected in a 3D accumulator array for the presence of circles with different centers and radii.
The function HoughCircles is used in OpenCV to detect the circles in an image. It takes the following parameters:
- image: The input image.
- method: Detection method.
- dp: the Inverse ratio of accumulator resolution and image resolution.
- mindst: minimum distance between centers od detected circles.
- param_1 and param_2: These are method specific parameters.
- min_Radius: minimum radius of the circle to be detected.
- max_Radius: maximum radius to be detected.
Python:
C++:
HoughCircles function has inbuilt canny detection, therefore it is not required to detect edges explicitly in it.
Circle Detection Result
The result of circle detection using Hough transform is shown below. The quality of result depends heavily on the quality of edges you can find, and also on how much prior knowledge you have about the size of the circle you want to detect.

Subscribe & Download Code
If you liked this article and would like to download code (C++ and Python) and example images used in this post, please click here. Alternately, sign up to receive a free Computer Vision Resource Guide. In our newsletter, we share OpenCV tutorials and examples written in C++/Python, and Computer Vision and Machine Learning algorithms and news.
Видео:Поиск объектов на видео с Python и TensorFlow с нуля, cтроим и обучаем нейросеть UNetСкачать

Обнаружение кругов с использованием OpenCV | питон
Обнаружение кругов находит множество применений в биомедицинских применениях, от обнаружения радужной оболочки до сегментации лейкоцитов. Применяемая методика аналогична той, которая используется для обнаружения линий, как обсуждалось в этой статье .
Основы обнаружения круга
Круг можно описать следующим уравнением:
Чтобы обнаружить круги, мы можем зафиксировать точку (x, y). Теперь нам нужно найти 3 параметра: a, b и r. Поэтому проблема в трехмерном пространстве поиска. Чтобы найти возможные круги, алгоритм использует трехмерную матрицу, называемую «Матрица накопителя», для хранения потенциальных значений a, b и r. Значение a (координата x центра) может варьироваться от 1 до строк, b (координата y центра) может варьироваться от 1 до столбцов, а r может варьироваться от 1 до maxRadius = 
Ниже приведены шаги алгоритма.
- Инициализация матрицы накопителя: Инициализация матрицы строк измерений * cols * maxRadius с нулями.
- Предварительная обработка изображения: примените к изображению размытие, оттенки серого и детектор краев. Это сделано для того, чтобы круги выглядели как затемненные края изображения.
- Цикл по точкам: выбрать точку
на изображении.
- Исправление r и прохождение циклов a и b: используйте двойной вложенный цикл, чтобы найти значение r, варьируя a и b в заданных диапазонах.
for a in range (rows):
for b in range (cols):
r = math.sqrt((xi — a) * * 2 + (yi — b) * * 2 )
Функция HoughCircles в OpenCV имеет следующие параметры, которые могут быть изменены в соответствии с изображением.
Detection Method: OpenCV has an advanced implementation, HOUGH_GRADIENT, which uses gradient of the edges instead of filling up the entire 3D accumulator matrix, thereby speeding up the process.
dp: This is the ratio of the resolution of original image to the accumulator matrix.
minDist: This parameter controls the minimum distance between detected circles.
Param1: Canny edge detection requires two parameters — minVal and maxVal. Param1 is the higher threshold of the two. The second one is set as Param1/2.
Param2: This is the accumulator threshold for the candidate detected circles. By increasing this threshold value, we can ensure that only the best circles, corresponding to larger accumulator values, are returned.
minRadius: Minimum circle radius.
maxRadius: Maximum circle radius.
Ниже приведен код для поиска кругов с использованием OpenCV на изображении выше.
import numpy as np
img = cv2.imread( ‘eyes.jpg’ , cv2.IMREAD_COLOR)
# Преобразовать в оттенки серого.
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Blur используя ядро 3 * 3.
gray_blurred = cv2.blur(gray, ( 3 , 3 ))
# Применить преобразование Хафа на размытое изображение.
cv2.HOUGH_GRADIENT, 1 , 20 , param1 = 50 ,
param2 = 30 , minRadius = 1 , maxRadius = 40 )
# Нарисуйте круги, которые обнаружены.
if detected_circles is not None :
# Преобразовать параметры круга a, b и r в целые числа.
for pt in detected_circles[ 0 , :]:
a, b, r = pt[ 0 ], pt[ 1 ], pt[ 2 ]
# Нарисуйте окружность круга.
cv2.circle(img, (a, b), r, ( 0 , 255 , 0 ), 2 )
# Нарисуйте маленький круг (радиус 1), чтобы показать центр.
cv2.circle(img, (a, b), 1 , ( 0 , 0 , 255 ), 3 )
Видео:Лабораторная работа "Обобщенное преобразование Хафа" Часть 1Скачать

Преобразование хафа для поиска окружностей python
Copy raw contents
Copy raw contents
[П]|[РС]|(РП) Преобразования Хафа
Преобразования Хафа — это метод нахождения линий, кругов и других простых форм на изображении (Хаф разработал данное преобразование для применения в физических экспериментах. Внедрение преобразования для решения задач компьютерного зрения осуществили Duda и Hart). Первоначально преобразование Хафа применялось для нахождения линий, т.к. является относительно быстрым способом нахождения прямых линий на бинарном изображении. В дальнейшем данное преобразование обобщили для более сложных задач, чем просто поиск линий.
Преобразование Хафа для линий
Теоретической подоплекой преобразования Хафа для линий является то, что любая точка на бинарном изображении, возможно, является частью некоторого множества линий. Если описать каждую линию по её наклону a и сдвигу b <Roman — наклон и пересечение (или наклон-сдвиг) — параметры уравнения прямой y = k•x + b, где k — угловой коэффициент прямой, вычисляемый через тангенс, а пересечение b — коэффициент сдвига прямой по оси y так, чтобы прямая пересекала ось y на высоте b>,то точка на исходном изображении преобразуется во множество точек на плоскости (a, b), соответствующие всем линиям, проходящих через эту точку (рисунок 6-9). Если преобразовать каждый ненулевой пиксель во входном изображении в такой набор точек в выходном изображении и просуммировать все подобные внесения, тогда линия, появившаяся на входном изображении (то есть на плоскости (x,y)) будет соответствовать локальному максимуму в выходном изображении (то есть на плоскости (a,b)). Поскольку суммируется вклад от каждой точки, плоскость (a,b) принято называть накопительной плоскостью (в дальнейшем просто накопитель).
Может оказаться, что плоскость вида наклон-сдвиг не лучший способ представления всех линий, проходящих через точку (из-за значительно различной плотности линий в зависимости от наклона и от того, что интервал возможных наклонов лежит в диапазоне от –∞ до +∞) . По этой причине, в численных расчетах используется другая параметризация преобразования изображения. Предпочтительная параметризация представляет каждую линию как точку в полярных координатах (ρ, θ), при чем эта линия проходит через указанную точку, но линия должна быть перпендикулярной к радиус-вектору от начала координат до этой точки на линии (рисунок 6-10). Уравнение для такой прямой:
Рисунок 6-9. Преобразование Хафа для линий находит множество линий на каждом изображении. Некоторые из них ожидаемые, но другие могут не быть таковыми
Рисунок 6-10. Точка (

Алгоритм преобразования Хафа не является явным для пользователя. Вместо этого он просто возвращает локальный максимум на плоскости (ρ, θ). Однако, необходимо понимать процесс преобразования, чтобы осознавать назначения входных аргументов функции, выполняющей преобразования Хафа для линий.
OpenCV поддерживает два вида преобразований Хафа для линий: обычное преобразование Хафа (SHT) и прогрессивное (улучшенное) вероятностное преобразование Хафа (PPHT). Ранее уже был рассмотрен алгоритм SHT. PPHT является его разновидностью и также вычисляет протяжённость каждой линии в дополнение к их наклону (рисунок 6-11). Алгоритм назван «вероятностным», т.к. вместо добавления каждой возможной точки на накопительную плоскость, он добавляет только часть из них. Идея состоит в том, что если существует максимум на плоскости, то, в любом случае, хотя бы частичное попадание в этот максимум будет достаточным условием, чтобы обнаружить линию; как результат — существенное снижение времени выполнения вычислений. Для обоих случаев в OpenCV существует одна функция, которая, в зависимости от входных параметров, принимает решение о выполнение того или иного метода.
Первый аргумент — это исходное изображение. Оно должно быть 8-битным, но при этом будет трактоваться как бинарное (т.е. все ненулевые значения будут восприниматься как равные единицы). Второй аргумент — указатель на место, где будет храниться результат, который может быть либо хранилищем в памяти (CvMemoryStorage из главы 8), либо матрицей размера Nx1 (при этом количество строк N будет также еще ограничивать максимальное число возвращаемых линий). Следующий аргумент method может быть CV_HOUGH_STANDARD, CV_HOUGH_PROBABLISTIC, CV_HOUGH_MULTI_SCALE для SHT, PPHT и многопараметрического варианта SHT (MSHT) соответственно.
Следующие два аргумента, rha и theta, устанавливают желательное разрешение для линий (т.е. разрешение накопительной плоскости). Параметр rho вычисляется в пикселях, а параметр theta в радианах, поэтому накопительную плоскость можно рассматривать как двухмерную гистограмму с ячейками размерностью rho пикселей на theta радиан. Значение параметра threshold определяет величину, при достижении которой сообщается о нахождении линии. Этот последний параметр на практике несколько мудрёный, при чем он не нормализуется, поэтому ожидается, что сам разработчик будет его масштабировать с учетом роста размерности входного изображения для алгоритма SHT. Помните, этот параметр, в действительности, определяет количество точек, которое должна содержать линия, чтобы быть добавленной в возвращаемый список линий.
Рисунок 6-11. Сначала выполнен проход при помощи детектора границ Canny (param1 = 50, param2 = 150), результат показан в оттенках серого. Затем произведено прогрессивное вероятностное преобразование Хафа (param1 = 50, param2 = 10), результат показан белым. Заметьте, что преобразование Хафа в основном правильно обнаруживает чёткие линии
Аргументы param1 и param2 алгоритм SHT не использует. Для алгоритма PPHT param1 задает минимальную длину для возвращаемого сегмента линии, а аргумент param2 задает расстояние между коллинеарными сегментами, необходимое для того, чтобы алгоритм не склеил их вместе в один сегмент большей длины. Для многопараметрического варианта SHT эти два параметра применяются для указания наивысшего разрешения до которого параметры возвращаемых линий должны быть вычислены. Многопараметрический SHT сначала вычисляет положение линий с учетом разрешений rho и theta, а затем начинает уточнение результатов до степени параметров param1 и param2 соответственно (т.е. конечное разрешение rho – это rho делённое на param1, а конечное разрешение для theta равно theta делённому на param2).
Возвращаемое значение функции зависит от входных параметров. Если параметр line_storage матрица, тогда возвращаемое значение будет NULL. В этом случае, матрица должна быть типа CV_32FC2 для SHT или многопараметрического SHT и CV_32SC4 для PPHT. В первых двух случаях величины ρ и θ для каждой линии будут помещены в двух каналах массива. В случае PPHT, четыре канала будут содержать значения x и y для начальной и конечной точек возвращаемого сегмента. И для всех этих случаев, количество строк в массиве будет обновлено функцией cvHoughLines2() до количества возвращаемых линий.
Если параметр line_storage содержит указатель на хранилище в памяти (более подробно об этом будет рассказано в главе 8), тогда возвращаемым значением будет указатель на структуру последовательности CvSeq. В этом случае, можно получить каждую линию или сегмент линии из последовательности при помощи подобной команды:
где lines это возвращаемое значение функции cvHoughLines2(), а i — индекс запрашиваемой линии. В этом случае, line будет указателем на данные запрашиваемой линии, при чем line[0] и line[1] будут действительными числами, соответствующие значениям ρ и θ (для SHT и MSHT), либо указателем на структуру из парных значений CvPoint для начальной и конечной точек сегмента (для алгоритма PPHT).
Преобразование Хафа для окружностей
Преобразование Хафа для окружностей (рисунок 6-12) работает почти аналогично только что описанному преобразованию Хафа для линий. «Почти» только лишь потому, что — если выполнить точно аналогичные действия — накопительная плоскость будет замещена плоскостью объема с тремя измерениями: одно для x, одно для y и последнее для радиуса круга r. Это приводит к значительно большим затратам памяти и значительно меньшей скорости выполнения. Реализация преобразования Хафа для окружности в OpenCV уходит от этой проблемы, применяя несколько хитрый метод, называемый градиентным методом Хафа.
Градиентный метод Хафа работает следующим образом. Вначале изображение проходит фазу поиска краев (использование функции cvCanny()). Затем для каждой ненулевой точки краев изображения ищется локальный градиент (вычисляется путем расчета производных Собеля первого и второго порядка для x и y при помощи функции cvSobel()). Используя этот градиент, каждая точка линии обозначается как наклон — от установленного минимума до указанного максимального расстояния — итерационно изменяя накопитель. В тоже время, запоминается расположение каждой ненулевой точки на изображении краев. Центры-кандидаты затем выбираются из тех точек (двухмерного) накопителя, величины которых выше заданного порога и, одновременно, больше всех их непосредственных соседей. Эти центры-кандидаты сортируются в порядке убывания их величины в накопителе, так, что центры с наибольшим количеством пикселей выбираются первыми. Далее, для каждого центра, анализируются все ненулевые пиксели. Эти пиксели сортируются в соответствии с их расстоянием от центра. Обрабатывая от наименьших расстояний до наибольших радиусов, выбирается единственный радиус, который лучше всего подходит ненулевым пикселям. Центр сохраняется, если он имеет достаточное количество ненулевых пикселей на краях на изображении и если расстояние от любого ранее выбранного центра удовлетворяет заданному значению.
Эта реализация позволяет алгоритму выполняться намного быстрее и, что еще более важно, позволяет обойти проблему разрастания трехмерного накопителя, что приводит к значительно большому зашумлению и нестабильно отражаемому результату. С другой стороны, этот алгоритм имеет несколько недостатков.
Рисунок 6-12. Преобразование Хафа для круга находит несколько кругов на тестовом шаблоне и (правильно) не находит ничего на фотографии
Во-первых, применение производных Собеля для вычисления локального градиента — и предположение, что он может быть рассмотрен как локальный тангенс — численно не стабильное решение. Он может давать верный результат «большую часть времени», при этом на выходе не исключено присутствие некоторого количества шума.
Во-вторых, каждый ненулевой пиксель на гранях на изображении рассматривается как центр-кандидат, поэтому для малого значения порога накопителя время выполнения алгоритма резко возрастет. В-третьих, поскольку для каждого центра выбирается только одна окружность, то в случае существования концентрических окружностей, используется только одна из них.
И наконец, поскольку центры рассматриваются в возрастающем порядке значений из накопителя и к тому же новые центры не добавляются, если они слишком близки к уже добавленным центрам, в случае концентрических кругов (либо около концентрических), предпочтение может отдаваться тем, у которых наибольший размер. (Указано «может» потому что существует некоторый шум, исходящий от производных Собеля; на гладком изображении с бесконечным расширением алгоритм будет определенным)
Принимая во внимание все выше сказанное, рассмотрим функцию OpenCV, которая реализует алгоритм Хафа для окружностей:
Функция преобразования Хафа для окружностей cvHoughCircles() имеет параметры, похожие на параметры в функции для линий. Исходное изображение должно быть 8-битным. Значительное отличие между cvHoughCircles() и cvHoughLines2() в том, что последняя функция запрашивает бинарное изображение. Функция cvHoughCircles() внутренне (автоматически) сама вызывает функцию cvSobel() (Внутренне вызывается функция cvSobel(), вместо cvCanny(). Это связано с тем, что cvHoughCircles() необходимо определить направление градиента для каждого пикселя, а это сложно выполнить для бинарной карты краев), поэтому вполне хватает и изображения в оттенках серого.
Аргумент circle_storage может быть либо массивом, либо хранилищем в памяти — зависит от предпочтений разработчика. Если массив, то он должен иметь одну колонку типа CV_32FC3; три канала используются для хранения значений положения и радиуса круга. Если хранилище в памяти, то окружности будут преобразованы в последовательности OpenCV, а функция cvHoughCircles() возвратит указатель на эту последовательность. (При указании в circle_storage указателя на массив, возвращаемым значением функции будет NULL). Аргумент method всегда должен быть равен CV_HOUGH_GRADIENT.
Аргумент dp является разрешением накопителя. Этот аргумент позволяет создавать накопитель более низких разрешений, чем исходное изображение. ((!)Есть смысл делать это, поскольку нет никаких оснований для существования окружностей, которые ровно подходят под количество категорий, таких как высота или ширина изображения сами по себе (!)). Если аргумент dp равен 1, тогда разрешение будет таким же, как и у исходного изображения; если аргумент dp больше 1, тогда разрешение будет в dp раз меньше (в случае dp = 2, будет половинным). Значение dp не может быть меньше 1.
Аргумент min_dist задает минимальное расстояние между двумя окружностями, чтобы алгоритм рассматривал их как две разные окружности.
Для применяемого (и требуемого на данный момент) метода CV_HOUGH_GRADIENT, следующие два параметра, param1 и param2, являются порогами для краев (Canny) и накопителя соответственно. В данном случае может смутить, что Canny сам по себе запрашивает два разных параметра для порогов. На самом деле внутренний вызов функции *cvCanny()*устанавливает в качестве верхнего порога значение равное param1, а нижний порог устанавливает равным половине величине param1. Параметр param2 применяется к накопителю в точно таком же смысле, как и параметр threshold для cvHoughLines().
Последние два параметра — это минимально и максимально возможные значения радиуса для окружностей, которые ищутся. Это означает, что они являются радиусами окружностей, для которых накопитель имеет представление. Пример 6-1 отражает пример использования функции cvHoughCircles().
Пример 6-1. Использование cvHoughCircles() для получения последовательности найденных окружностей на изображение в оттенках серого
Стоит заострить внимание на том, что независимо от все возможных применяемых приемов, описать окружности можно только при помощи трех степеней свободы (x, y и r), в то время как для линий достаточно только двух (ρ и θ). Как результат, алгоритм поиска окружностей, по сравнению с алгоритмом поиска линий, затрачивает на выполнение больше времени и памяти. Принимая во внимание данный факт, неплохо было бы ограничивать радиус окружности насколько это возможно в той или иной ситуации (Хотя cvHoughCircles() улавливает центры достаточно точно, он иногда не способен найти правильный радиус. Поэтому в приложениях, где требуется только нахождение центра (либо там, где для нахождения радиуса можно применить другие механизмы), величину радиуса, возвращаемую cvHoughCircles можно игнорировать). Преобразование Хафа было расширено произвольными формами Балларда в 1981, в основном рассматривая формы, как наборы градиентных граней.
🔥 Видео
Лекция 9 Канни, Хаф, Харрис,SIFTСкачать

Компьютерное зрение. Пишем распознавание дорожной полосы на Python (cv2)Скачать

Распознавание текста с изображения на Python | EasyOCR vs Tesseract | Компьютерное зрениеСкачать

Учим программу распознавать текст на картинках, видео, играх ▲ Python + OpenCV + TesseractСкачать

Урок №10. Распознавание и отслеживание объектов по форме. Beyond RoboticsСкачать
Подсчёт объектов на изображении Python | Компьютерное зрениеСкачать

Лабораторная работа "Обобщенное преобразование Хафа" Часть 3Скачать

Изучение Python OpenCV / Урок #2 – Работа с изображениями и видеоСкачать

Изучение Python OpenCV / Урок #3 – Создание объектов и вывод информацииСкачать

РАСПОЗНАВАНИЕ АВТОМОБИЛЬНЫХ НОМЕРОВ С ПОМОЩЬЮ PYTHON | КОМПЬЮТЕРНОЕ ЗРЕНИЕ | PYTESSERACT, OPENCVСкачать

УРОК 2. Как сделать АВТОКЛИКЕР для Windows, Linux, macOS! Кликаем по изображениям! Python pyautogui!Скачать

Строим Нейронную Сеть для Распознавания Изображений за 20 минутСкачать

Компьютерное зрение. Python. Поиск объектов на изображении. Mediapipe. Find face in the image. Test.Скачать

Распознавание объектов на Python / Глубокое машинное обучениеСкачать


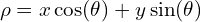
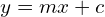
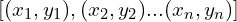
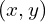 coordinates of the center of the circle.
coordinates of the center of the circle.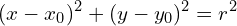

 на изображении.
на изображении.


