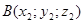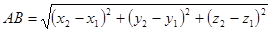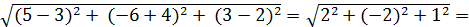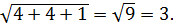МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО
Разработал преподаватель: Игнатьева Елена Сергеевна
Решение задач по теме: «Уравнение окружности, сферы, плоскости. Расстояние между точками»
— применить умения в использовании теоретических сведений для составления уравнений окружности, сферы, плоскости.
1. Рабочая тетрадь в клетку
2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.
3. Калькулятор простой.
I Вариант II Вариант
1. Дан ∆ ABC с вершинами в точках Дан ∆ ABC с вершинами в точках
A (7; 3; -2) A (2; 0; 5)
B (1; 3; 6) B (3; 4; 0)
С (0; 0; -1). C (2; 4; 0).
Найти длину средней линии, Найти длину средней линии,
параллельной AB . параллельный BC .
2. Составить уравнение плоскости, Составить уравнение плоскости,
проходящей через точку А и проходящей через точку В и
перпендикулярный вектору AB , перпендикулярный вектору AB ,
если А(2; 3; -4), В(-1; 2; 2). если А(-2; 1; 3), В(1; -2; 4).
3. Сфера задана уравнением
( x -1) 2 + y 2 +( z -2) 2 = 9 x 2 +( y +3) 2 +( z -2) 2 = 25
a ) Назовите координаты центра и радиус сферы.
б) Определите, принадлежит ли данной сфере точки:
1. Внимательно прочитать тему и цель практической работы .
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
1.Расстояние между точками.
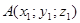
AB =
2. Уравнение плоскости.
Уравнение плоскости, проходящей через данную точку и перпендикулярной данному вектору.
Ненулевой вектор n, перпендикулярный плоскости, называют ее нормальным вектором. Если дана точка М(х0;у0; z 0) и нормальный вектор n = (A, B, C) плоскости, то ее уравнение имеет вид A ( x — x 0 ) + B ( y — y 0) + C ( z — z 0)
Равенство выражает необходимое и достаточное условие перпендикулярности двух векторов n и M 0 M .
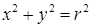
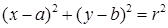
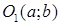
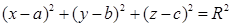
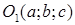
При выполнении практической работы рассмотрите следующие примеры:
Дан ∆АВС с вершинами в точках А(3; -4; 2), В(-5; 6; 7), С(5; -6; 3).
Найти длину средней линии, параллельной АС.
MN — средняя линия
AC =
=
Составить уравнение плоскости, проходящей через точку M (1; -2; 4) и перпендикулярный вектору MN , N (3; 4; 5).
MN=(3-1; 4+2; 5-4); MN=(2; 6; 1); a=2; b=6; c=1.
Сфера задана уравнением
( x +2) 2 +( y -5) 2 + z 2 =16.
а) Назовите координаты центра и радиус сферы.
б) Определите принадлежат ли данной сфере точки: А(-2; 9; 0) и В(1; 3; 2)
а) (-2; 5; 0) – координаты центра.
R = 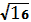
(-2+2) 2 +(9-5) 2 +0 2 =16
А принадлежит сфере.
(1+2) 2 +(3-5) 2 +2 2 =16
В не принадлежит 17=16 (неверно).
Вопросы для закрепления теоретического материала к практическому занятию:
1. Записать формулу расстояния между точками.
2. Уравнение плоскости.
3. Уравнение окружности.
4. Уравнение сферы.
Название практической работы.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
1. Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.
2. Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.
3. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
4. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
5. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
6. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017
7. Башмаков М.И. Математика: Учебник. — М., 2016.
Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Практическая работа №28 по теме: Уравнение прямой и окружности
Выполните на листах для практических работ. Принести после карантина.
Практическая работа №28
по теме: Уравнение прямой и окружности
Цель: изучить теоретические основы темы и выполнить задания по теме.
1 Изучите теоретические основы темы и примеры решения задач. Сделайте записи в тетрадь
Основные теоретические положения
Используем два уже известных факта и выведем уравнение окружности:
1. Все точки окружности находятся в данном расстоянии (радиус) от данной точки (центр);

Допустим, что центр окружности находится в точке C(xC;yC), а радиус окружности равен R.
Любая точка P(x;y) на этой окружности находится на расстоянии R от центра C, значит справедливо равенство
Это и есть уравнение окружности с центром C и радиусом R. Координаты всех точек, которые находятся на окружности, удовлетворяют уравнение.
Если центр окружности находится в начале координат (0;0), то уравнение окружности имеет вид x2+y2=R2


Упростим уравнение – раскроем скобки и приведем подобные слагаемые, получим:




Тогда уравнение прямой примет вид: 
2 Выполните задания
1. Закончите фразу, чтобы получилось верное высказывание:
Уравнение 
2. Начертите прямую, заданную уравнением y – x + 3 = 0.
3. Среди следующих утверждений укажите истинные и ложные:
а) уравнение окружности в декартовых координатах имеет вид 
б) прямые, задаваемые уравнениями y = 5x – 4 и y = 5x + 2, пересекаются.
4. Приведите уравнение прямой 12x – 5y – 65 = 0 к виду y = kx + b (выберите ответ).
Ответы: а) y = 12x + 65; б) 
Видео:Уравнение окружности (1)Скачать

Решение задач по теме: «Уравнение окружностей»
Разделы: Математика
За неделю до проведения урока класс делится на четыре группы. Каждая готовит презентацию, отражающую название команды.
1. Образовательные:
2. Развивающие:
3. Воспитательные:
Ход урока
I. Организационный момент.
В начале урока выдается командам оценочный лист ( Приложение 1 ) с целью самостоятельной оценки учащимися степени участия каждого члена команды в подготовке к уроку и его проведении.
Рассказываются правила урока. За каждое правильное решение команде выдается лепесток определенного цвета:
все ответы верные – красный;
одна ошибка – зеленый;
две ошибки – жёлтый.
Лепестки крепятся на магнитную доску, образуя цветок.
Итоговая оценка выставляется с учетом этого бланка, а также учитывается количество и цвет набранных командой лепестков в цветке на доске.
2. Знакомство с командами (представление презентаций, Приложение 2 ).
3. Актуализация знаний учащихся.
– На последних уроках геометрии мы познакомились с еще одним способом решения задач МЕТОДОМ КООРДИНАТ.
Задавая фигуры уравнением и выражая в координатах геометрические соотношения, мы применяем алгебру к геометрии. Так мы поступили, когда выразили через координаты основную геометрическую величину – расстояние между точками, а затем, когда вывели уравнение окружности и прямой.
Пользуясь координатами, можно истолковывать уравнения и неравенства геометрически и таким образом применять геометрию к алгебре и анализу. Графическое изображение функций – первый пример такого применения метода координат
Метод координат в соединении с алгеброй составляет раздел геометрии, называемый “Аналитической геометрией”.
Сегодня я предлагаю еще раз поговорить об уравнении окружности и проследить, как алгебра помогает в решении геометрических задач.
4. Разминка.
– На доске записан ряд уравнений. Какие фигуры они задают?
Команды получают карточки с заданием. Время обдумывания 2мин.
По истечению времени идет опрос команд по очереди.
1  | 7.  |
2 . . | 8.  |
3.  | 9.  |
4.  | 10.  |
5.  | 11.  |
6.  | 12. |

Учитель показывает как, выделив полный квадрат, получить уравнение окружности.
Оценить результат работы команд.
Выясните, будет ли данные уравнения задавать окружность, если да, то укажите радиус и координаты центра. Если нет, то почему?
Каждая из команд получают свою карточку. Время 7 минут.
1.  | 1.  |
2.  | 2.  |
3.  | 3.  |
1.  | 1.  |
2  | 2  |
3  | 3  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Последние уравнение в каждой карточке не задает окружность, и учащиеся поясняют почему. Оценить ответы.
1. Как могут взаимораспологаться две окружности? Дается время(3 мин.). Предлогается ребятам нарисовать различные варианты на ватмане и показать рисунки. После демонстрации и обсуждения всевозможных вариантов Предлогается следующая задача.
2. Как взаиморасположены линии заданные уравнениями?

Изобразите ответ на обратной стороне ватмана (на нем, заранее, нанесена система координат.)
Ответ:
O
Значит: первая внутри второй.
Результат этого задания оценивается следующим образом:
Команда, выполнившая первая – красный; вторая – зеленый; третья – желтый
После подведения итогов предлагается задача общая для всех команд.
Командам выдается карточка с кратким описанием условия. Текст задачи зачитывается.
Окружность задана уравнением 
Точка с координатами (5;4) является центром другой окружности касающейся первой внешним образом. Напишите уравнение этой окружности.
Вопросы для обсуждения:
-Поможет ли рисунок в решении задачи?
-Что можно узнать из уравнения первой окружности?
-Что надо знать, чтобы записать уравнение второй окружности?
-Как можно узнать радиус второй окружности?
Ответ:
Перед следующим заданием полезно повторить:
Какая окружность называется описанной около треугольника?
Что значит, точка принадлежит графику уравнения?
Что необходимо знать для написания уравнения окружности?
Написать уравнение окружности описанной около треугольника с заданными координатами вершин.
Какие, алгебраические, приемы могут быть использованы для решения поставленной задачи? (составление систем уравнений и приемы их решения).
| 3. С (3;-7) | 4. В (1;-4) |
| Д (8;-2) | К (4;5) |
| К (6;2) | Д (3;-2) |
1.  | 2.  |
3.    | 4 . . |
Следующую задачу решает учитель.
Задача: Что представляет собой множество точек плоскости, отношение расстояний от которых до двух данных точек есть величина постоянная?
Решение: Впервые эту задачу сформулировал и решил Аполлоний Пергский, (260-170 гг. до н.э.)
Решение получилось очень сложное – поскольку применены геометрические приемы. Однако в работах французского математика Рене Декарта эта задача решена более элегантно. Декарт применил метод координат.
Я предлагаю посмотреть на это решение. Итак, пусть даны две точки ,А и В и некоторое положительное число k, равное отношению расстояний до точки М.
1случай. Если k=1,тогда множество точек М есть серединный перпендикуляр к отрезку АВ.
2 случай. Пусть k целое не отрицательное число не равное 1
Для удобства решения возьмем k=2 , т.е. МА: МВ=2.
Введем систему прямоугольных координат. Совместим начало отсчета с точкой В. В качестве положительной полуоси x возьмем луч ВА. (рис.2)
Тогда получим следующие координаты точек: В(0,0), А(a,0), М(x,y). Пусть a=3 опять для простоты рассуждений.
Тогда, пользуясь формулами расстояния между двумя точками, запишем:

Получили уравнение окружности с центром в точке (-1;0) и радиусом r=2.
Значение радиуса не случайно вспомним, что мы выбрали k=2.
Решая задачу в общем виде т.е. при условии ,что точка А имеет координаты (a;0) и k

Такая окружность называется окружностью Апполония.
Подводится итог урока. Выставляются оценки.
📽️ Видео
9 класс, 6 урок, Уравнение окружностиСкачать

Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Уравнение окружности. Практика. Урок 7. Геометрия 9 классСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать

Уравнение окружностиСкачать

УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

9 класс, 7 урок, Уравнение прямойСкачать

Составляем уравнение окружностиСкачать

№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Математика это не ИсламСкачать

Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать

УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать

Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать