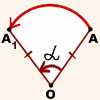
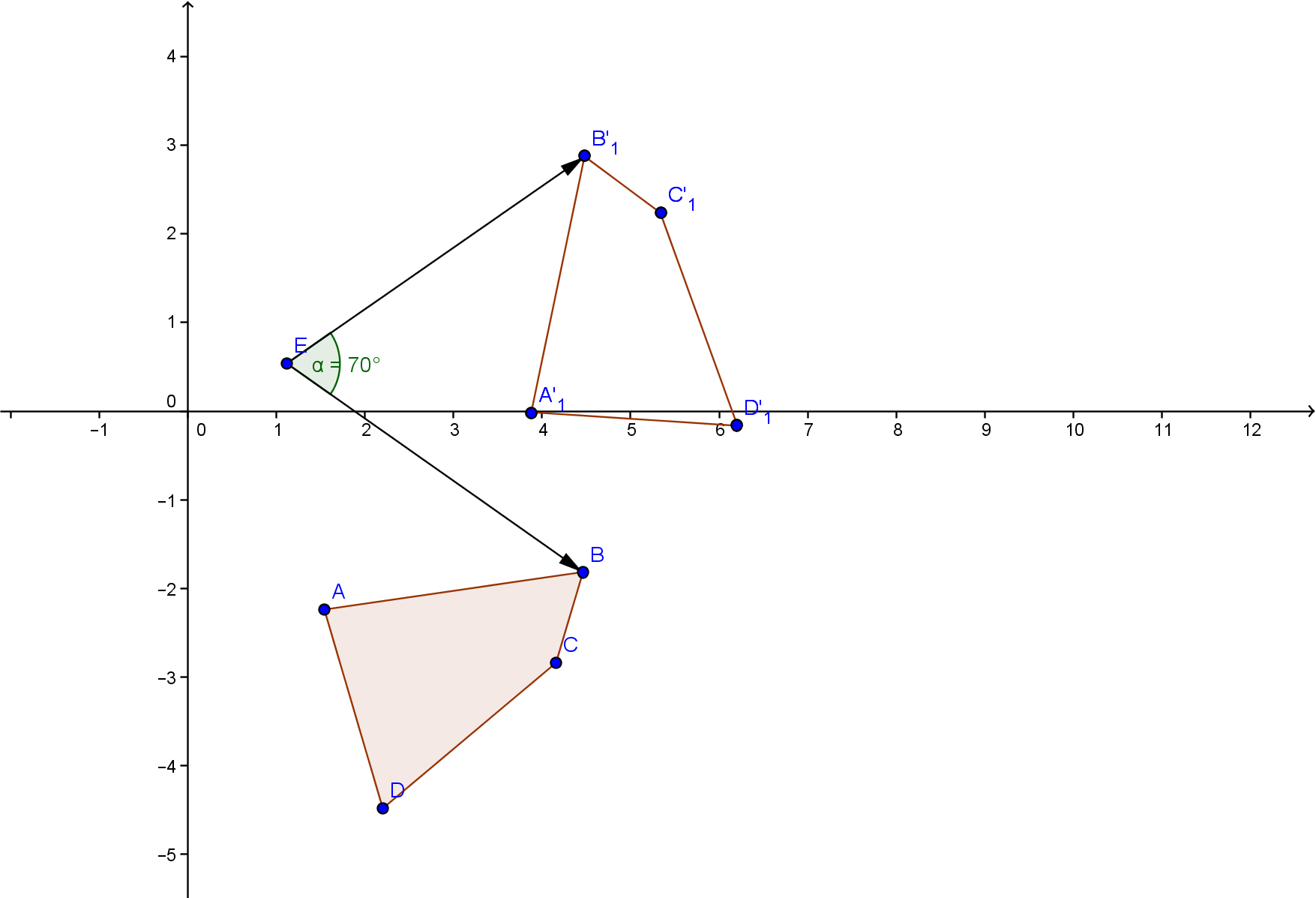
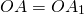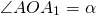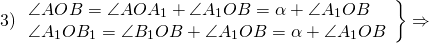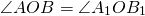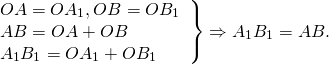Отметим на плоскости точку O — центр поворота. Зададим угол α — угол поворота.
Поворот плоскости вокруг точки O на угол α — это отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, что
При этом точка O остаётся на месте (отображается сама в себя), а все остальные точки поворачиваются вокруг точки O в одном и том же направлении — либо по часовой стрелке, либо против часовой стрелки.
Поворот является движением
(то есть отображением плоскости на себя, сохраняющим расстояние).
Если точки A, O и B не лежат на одной прямой.
Пусть точка O — центр поворота, α — угол поворота. При повороте вокруг точки O на угол α против часовой стрелки точка A отобразится в точку A1, точка B — в точку B1.
Проведём отрезки AB и A1B1.
Рассмотрим треугольники AOB и A1OB1.
2) OB=OB1 (по определению поворота).
Следовательно, треугольники AOB и A1OB1 равны (по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон: AB=A1B1.
Если точки A, O и B лежат на одной прямой.
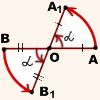
При повороте в направлении по часовой стрелке все рассуждения аналогичны.
Равенство A1B1=AB означает, что при повороте расстояние между точками сохраняется, а значит, поворот является движением.
Видео:Поворот фигуры. Построить поворот фигур вокруг точки на угол по часовой или против часовой стрелкиСкачать
Поворот точек на произвольный угол онлайн
| Координаты фигуры, разделенные через пробел |
| Угол поворота в градусах (если положительное то против часовой стрелки) |
| Точка относительно которой проводится поворот |
| Новые координаты полученные при повороте фигуры(точки) на заданный угол |
Поворот — это движение фигуры в пространстве вокруг неподвижной точки, принадлежащей этому же пространству.
Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать  СинтаксисКоординаты — строка, содержащая координаты в виде x:y (где x — абсцисса координаты, y — ордината координаты), разделенные хотя бы одним пробелом Точка вращения — точка, относительно которой будет осуществляться поворот, всех заданных координат. Поворот в градусах — поворот фигуры на заданный угол. Если число положительное — то поворот производится ПРОТИВ часовой стрелке, если отрицательный, то ПО часовой стрелке. Видео:9 класс, 33 урок, ПоворотСкачать  ПримерыПример: задан треугольник следующими координатами A(1:1) B (5:5) C(0:7) Необходимо повернуть треугольник на 30 градусов против часовой стрелки относительно точки с координатами 3:3 Видео:Поворот | Обоснование | ПрименениеСкачать  Геометрия. 9 классОтметим на плоскости точку О – центр поворота и зададим угол α – угол поворота. Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что ОМ = ОМ1 и угол МОМ1 равен α. Этот вид отображения плоскости на себя называется поворотом. При этом точка М отображается в точку М1. 1. Проведем луч ОА. При этом точка А отображается в точку А1, точка отображается в точку В1, точка С отображается в точку С1. 📸 ВидеоПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС И ПОВОРОТ 9 класс геометрия АтанасянСкачать  ПоворотСкачать 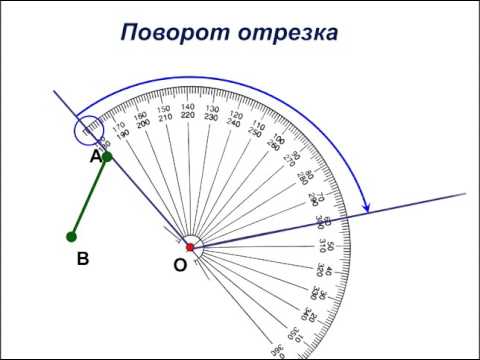 Параллельный перенос. Симметрия. Поворот | МатематикаСкачать  Построение треугольника, симметричного данному относительно точки, принадлежащей его сторонеСкачать  ВПР 6 класс. 12 задание. Фигура симметиичная данной относительно оси.Скачать  Поворот фигуры в PowerPoint вокруг вершиныСкачать  Центральная симметрия. 6 класс.Скачать  #192 ПОВОРОТ И ПЕРЕНОС // ТРЕУГОЛЬНИКСкачать  Пошаговая схема поворота на 150° против часовой стрелки.Скачать  Построение натуральной величины треугольника методом вращенияСкачать  Симметрия относительно точки (центральная симметрия). Пример 2Скачать  8 класс, 9 урок, Осевая и центральная симметрияСкачать  Симметрия относительно точки. 6 классСкачать  Геометрия 8 класс (Урок№7 - Осевая и центральная симметрия.)Скачать  Математика 6 Поворот и центральная симметрияСкачать  ГомотетияСкачать  |
