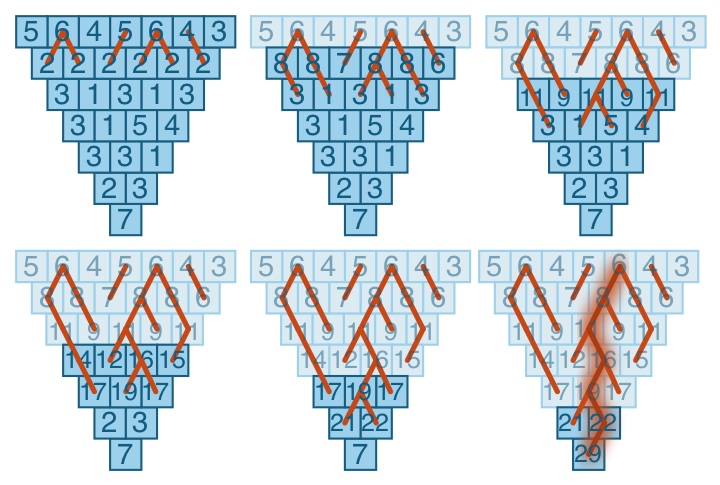Решение на питоне заданий из модуля 7.9 с сайта stepik.org из курса «Поколение python: курс для начинающих». Предыдущий модуль 7.8.
Численный треугольник 3
Дано натуральное число nn. Напишите программу, которая печатает численный треугольник с высотой равной nn, в соответствии с примером:
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
16 17 18 19 20 21
…
Формат входных данных
На вход программе подается одно натуральное число.
Формат выходных данных
Программа должна вывести треугольник в соответствии с условием.
Примечание. Используйте вложенный цикл for.
Численный треугольник 4
Дано натуральное число nn. Напишите программу, которая печатает численный треугольник с высотой равной nn, в соответствии с примером:
1
121
12321
1234321
123454321
…
Формат входных данных
На вход программе подается одно натуральное число.Формат выходных данных
Программа должна вывести треугольник в соответствии с условием.
Примечание. Используйте вложенный питон цикл for.
Делители-1 ?️
На вход программе подается два натуральных числа aa и bb (a while .
Сумма факториалов
Дано натуральное число nn. Напишите программу, которая выводит значение суммы 1!+2!+3!+ldots+n!1!+2!+3!+…+n!.
Формат входных данных
На вход программе подается одно натуральное число.
Формат выходных данных
Программа должна вывести значение суммы 1!+2!+3!+ldots+n!1!+2!+3!+…+n!.
Примечание 1. Факториалом натурального числа nn, называется произведение всех натуральных чисел от 11 до nn, то естьn!=1cdot2cdot3cdot…cdot nn!=1⋅2⋅3⋅…⋅n
Примечание 2. Задачу можно решить без вложенного цикла. Напишите две версии программы =)
Простые числа
На вход программе подается два натуральных числа aa и bb (a
Видео:7.9 Численный треугольник 4. "Поколение Python": курс для начинающих. Курс StepikСкачать

Программа Python для печати треугольника Паскаля
В этом руководстве мы обсудим, как напечатать треугольник Паскаля с помощью программы Python. Но сначала давайте разберемся, что такое треугольник Паскаля.
Видео:7.9 Численный треугольник 3. "Поколение Python": курс для начинающих. Курс StepikСкачать

Вступление
Треугольник Паскаля – это захватывающая математическая концепция, в которой треугольный массив формируется путем суммирования смежных элементов в предыдущей строке. Проще говоря, каждое число генерируется путем суммирования соседней строки, а внешние края треугольника всегда равны 1. Он назван в честь известного французского математика Блеза Паскаля. Ниже представлен треугольник Паскаля.
На изображении выше первая строка равна 1. Вторая строка содержит 2 единицы, а третья строка – 1 2 1, которая формируется путем суммирования указанной выше строки. Таким образом, он следует альтернативному шаблону во всем треугольнике и так далее.
Видео:#26. Треугольник Паскаля как пример работы вложенных циклов | Python для начинающихСкачать

Алгоритм печати треугольника Паскаля в Python
Ниже приведен шаг, используемый для печати треугольника Паскаля.
- Шаг – 1: Получение данных от пользователя для определения количества строк.
- Шаг – 2: Объявление пустого списка, в котором будут храниться значения.
- Шаг – 3: Используя цикл for, который будет перебирать от 0 до n – 1, добавить подсписки в список.
- Шаг – 4: Теперь добавить 1 в список.
- Шаг – 5: Используя цикл for, определить значение числа внутри соседней строки треугольника.
- Шаг – 6: Распечатать треугольник Паскаля в соответствии с форматом.
- Шаг – 7: Выход.
Давайте разберемся с реализацией алгоритма в программе Python:
Запускаем программу еще раз.
В приведенной выше программе мы взяли несколько строк от пользователя в качестве входных. Мы объявили пустой список. Затем мы использовали цикл for, который добавлял подсписок в пустой список. Следующий добавляется ко всем подспискам. Внутренний цикл for определил, что число внутри треугольника является суммой соседней строки выше. В конце концов, мы использовали цикл for для печати треугольника Паскаля в соответствии с форматом.
Способ 2
Мы можем использовать другой метод, следуя биномиальному коэффициенту, вся строка начинается с 1, а i-я запись в строке номера строки – это биномиальный коэффициент C(строка, i). Формула приведена ниже.
Временная сложность указанного выше метода равна 0(N2).
Способ 3
Этот метод является оптимизированным способом печати треугольника Паскаля. Этот метод основан на степени 11.
Как мы можем видеть в приведенном выше коде, когда мы вводим количество строк пять. Это дало неверный результат. Это означает, что он работает только до n
Видео:Треугольник ПаскаляСкачать

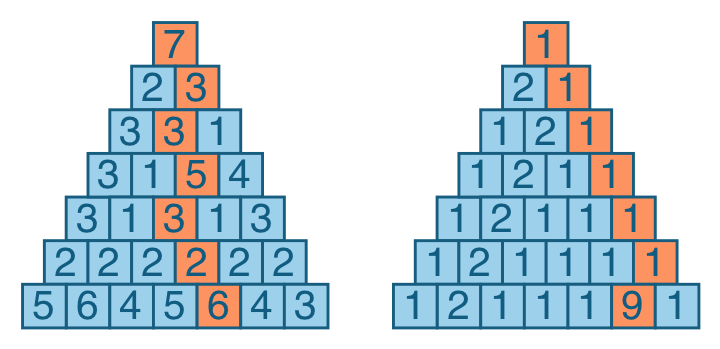
Золотая пирамида — задача про треугольник, составленный из чисел
В этом выпуске рассмотрим классическую задачу, известную под названием «Золотая гора». На CheckiO её реализовали в этой задаче.
Представьте себе треугольник, составленный из чисел. Одно число расположено в вершине. Ниже размещено два числа, затем три, и так до нижней грани. Вы начинаете на вершине, и нужно спуститься к основанию треугольника. За каждый ход вы можете спуститься на один уровень и выбрать между двумя числами под текущей позицией. По ходу движения вы «собираете» и суммируете числа, которые проходите. Ваша цель — найти максимальную сумму, которую можно получить из различных маршрутов.
Рассмотрим различные методы решения.
Рекурсия
Первым делом в голову приходит мысль использовать рекурсию и просчитать все пути от вершины. Когда мы спускаемся на один уровень, то все доступные числа ниже образуют новый меньший треугольник, и можно запустить нашу функцию уже для нового подмножества и так пока не достигнем основания.
Как мы видим, на первом уровне мы запустим нашу функцию два раза, затем 4, 8, 16 раз и так далее. В итоге мы получим сложность алгоритма 2 N и, например, для 100-уровневой пирамиды нам нужно будет уже где-то ≈10 30 вызовов функции. Многовато.
Динамическое программирование
Что если попробовать использовать принцип динамического программирования и разбить нашу проблему на множество мелких подзадач, результаты которых мы затем аккумулируем. Попробуйте взглянуть на треугольник вверх ногами. А теперь на второй уровень (то есть предпоследний от основания). Для каждой ячейки мы можем решить, каким будет лучший выбор в наших маленьких трёхэлементных треугольничках. Выбираем лучший, суммируем с рассматриваемой ячейкой и записываем результат. Таким образом, мы получили наш треугольник, но на один уровень ниже. Повторяем данную операцию снова и снова. В результате нам нужно (N-1)+(N-2)+…2+1 операций и сложность алгоритма равна N 2 .
Решения игроков CheckiO
Пользователь gyahun_dash написал интересную реализацию описанного выше метода ДП в своем решении «DP». Он использовал reduce, чтобы проходить по парам строк, и map чтобы обработать каждую из них.
Игрок evoynov использовал двоичные числа, чтобы перебрать все возможные маршруты, представленные как последовательность 1 и 0 в своем решении «Binaries». И это наглядный пример сложности алгоритма с рекурсией и перебором всех маршрутов.
И чтобы не было скучно, посмотрим на легкий мозгодробитель от пользователя nickie и его однострочник «Functional DP», который только формально состоит из двух строк. Конечно, это решение из категории «Творческих» («Creative»). Не думаю, что автор использует такое на боевом коде. А просто для так для веселья, почему бы и нет.
Вот и всё на сегодня. Делитесь вашими идеями и мыслями.
Спасибо CheckiO за интересную задачу.
🎬 Видео
7.8 Звездный треугольник. "Поколение Python": курс для начинающих. Курс StepikСкачать

7.8 Численный треугольник 1. "Поколение Python": курс для начинающих. Курс StepikСкачать

4.3 Треугольник Паскаля 1. "Поколение Python": курс для продвинутых. Курс StepikСкачать
7.1 Звездный треугольник. "Поколение Python": курс для начинающих. Курс StepikСкачать
14.1 Звездный треугольник. "Поколение Python": курс для начинающих. Курс StepikСкачать

4.3 Вид треугольника. "Поколение Python": курс для начинающих. Курс StepikСкачать
Как нарисовать треугольник на языке python? | треугольник на питонеСкачать

числовой треугольник в PythonСкачать

Решение простых задач на python | Площадь и периметр прямоугольного треугольникаСкачать

28 Вложенные циклы PythonСкачать

Треугольник Паскаля Python. Коэффициенты для Бинома НьютонаСкачать

13.1 Звездный треугольник 1. "Поколение Python": курс для начинающих. Курс StepikСкачать

13.2 Звездный треугольник. "Поколение Python": курс для начинающих. Курс StepikСкачать

Найти площадь прямоугольника, треугольника или круга. Решение задачи на PythonСкачать
Треугольник Паскаля на PythonСкачать

6.1 Площадь треугольника. "Поколение Python": курс для начинающих. Курс StepikСкачать