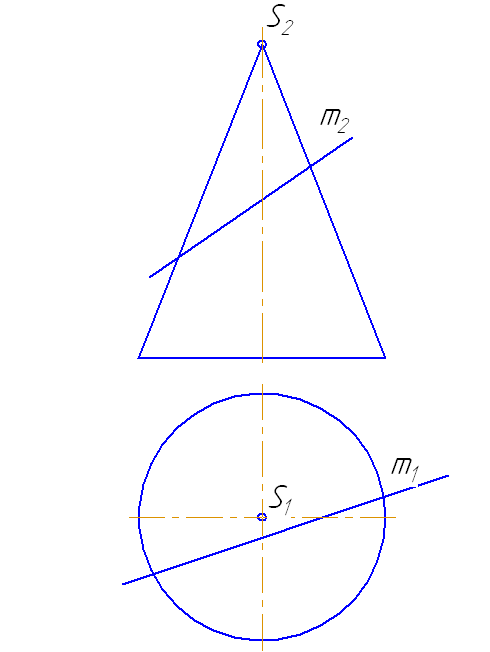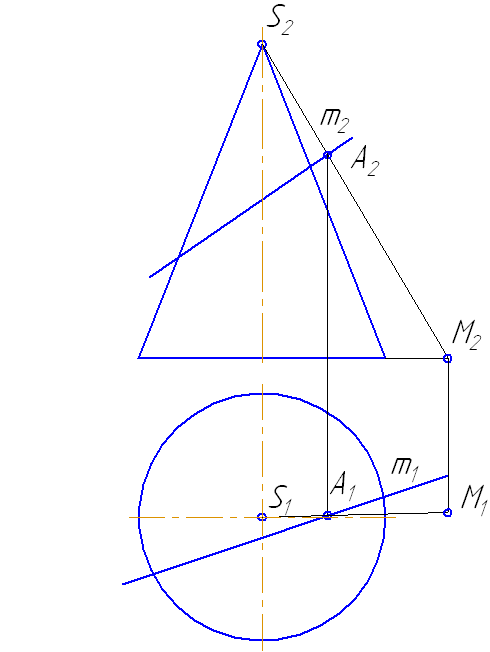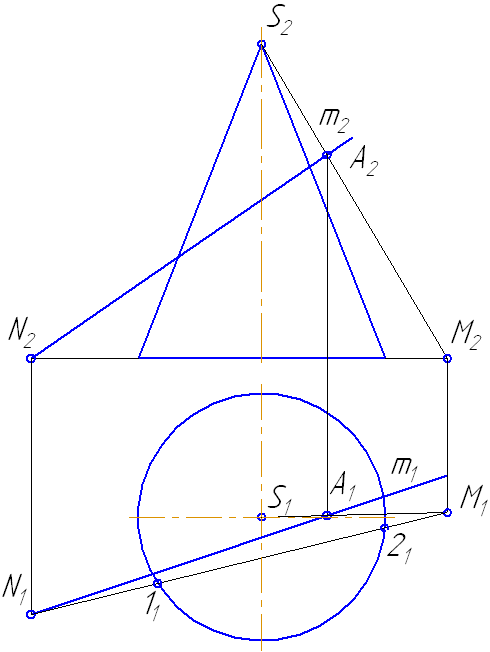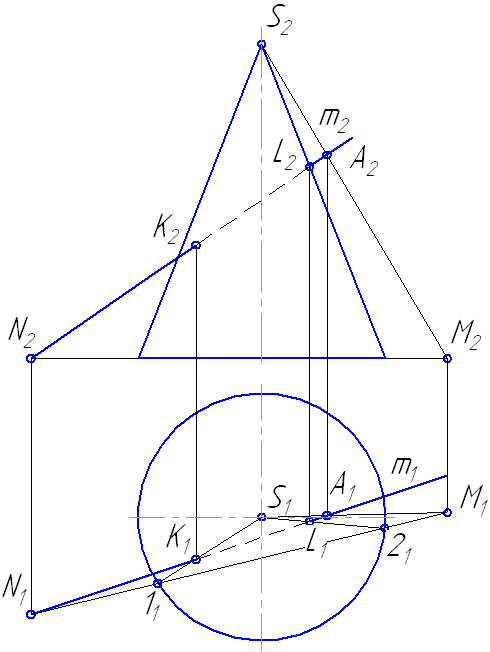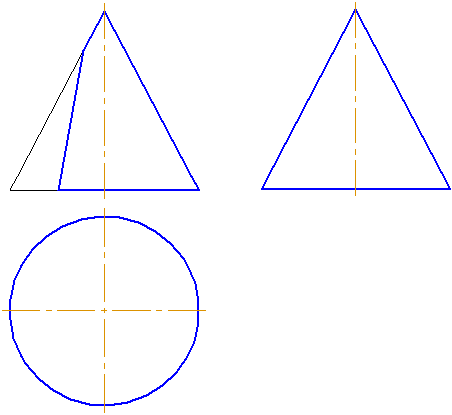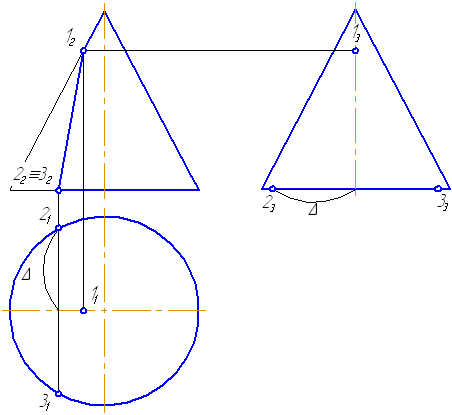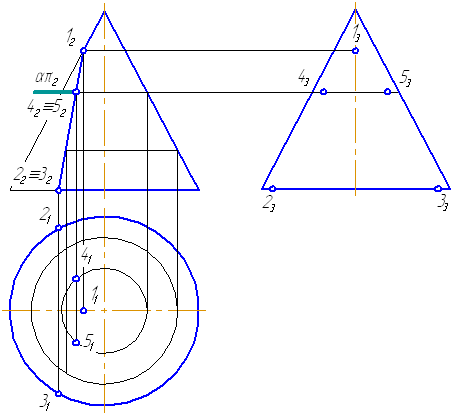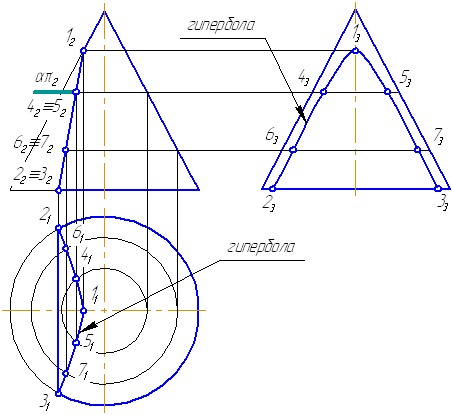Поверхности образующиеся перемещением окружности постоянного или переменного радиуса носят название

Параметризация

1. С помощью параметризации осуществляется оценка:
   1. Формы, положения оригинала и его частей.
2. Согласно теории параметризации, по отношению друг к другу параметры:
   1. Независимы.
3. Процесс измерения параметров начинается:
   1. Назначения системы параметризации.
4. Система параметризации выбирается вне оригинала при определении:
   1. Параметров положения
5. На чертежах параметры реализуются:
   1. Условными обозначениями, геометрическими условиями, размерами.
6. Связь между количеством параметров, необходимых для выделения из множества фигур единственной фигуры, количеством параметра формы ПФ, положения ПП, параметров, заменяемых геометрическими условиями ГУ, выражается соотношением:
   1. П = ПП + ПФ — ГУ.
7. Система параметризации называется связанной с оригиналом при определении:
   1. Параметров формы.
8. Количество параметров, позволяющих определить положение произвольной точки в пространстве, носит название:
   1. Размерность пространства.
9. Процесс и результат задания параметров для какого – либо оригинала называют:
   1. Параметризация
10. В зависимости от вида задания параметры бывают
    1. Формальные или действительные
11. Условия, возникающие между элементами оригиналов воспринимаемые на глаз сопровождаемые условными обозначениями, называют
    1. Геометрическим

Аксонометрия

1. Классификация аксонометрических изображений на изометрию, диметрию, триметрию производится на основании:
   1. Соотношения показателей по всем осям.
2. Показатели искажения по всем осям различны в:
   1. Триметрии.
3. Классификация аксонометрии на прямоугольную и косоугольную производится на основании:
   1. Направления проецирующих лучей по отношению к плоскости проекций.
4. Показатели искажения по всем осям одинаковы в:
   1. Изометрии.
5. Аксонометрический чертеж оригинала получают на:
   1. Одной плоскости проекций.
6. Вторичной проекцией точки называется:
   1. Проекция проекции точки на любую координатную плоскость.
7. Аксонометрические оси – это:
   1. Аксонометрические проекции осей натуральной системы координат.
8. Аксонометрия может быть получена проецированием:
   1. 2. Только параллельным.
9. Сущность метода аксонометрии состоит в том, что оригинал относят к некоторой системе координат и затем проецируют на плоскость проекций вместе с:
   1. 2. Координатной системой.
10. Основой для вторичной проекции аксонометрии оригинала может служить:
    1. Любой из стандартных видов.
11. Аксонометрию оригинала получают на:
    1. Одной плоскости проекций
12. Классификация аксонометрий на прямоугольные и косоугольные производится на основании:
    1. величины угла
13. Выберите из предложенных коэффициентов искажения по осям фронтальной динаметрического проекции
    1. 1;0,5;1
14. Вторичная горизонтальная точка проекции А строится по
    1. Абсциссе орденате и аппликате
15. Плоскость на которой получаются аксонометрическую проекцию называют
    1. аксонометрическая
16. Основой для вторичной проекции точки являются
    1. Проекции точки на любую из координатных плоскостей

К линейчатым поверхностям относят:

Множество линий, заполняющих поверхность так, что через каждую точку поверхности в общем случае проходит одна линия этого множества, носит название:

Образующая поверхность вращения может быть:

Плоской и пространственной кривой.

Линейчатая поверхность в общем случае однозначно определяется:

Конечное множество точек, задающих поверхность, носит название:

2. Точечного каркаса.

Очерк поверхности – это:

2. Проекции поверхности.

В начертательной геометрии классификация поверхностей производится на основании:

2. Формы образующих и закона образования.

Геликоиды – это винтовые поверхности, образующими которых являются:

Поверхности, образующими которых являются прямые линии, называются:

Поверхности, образующими перемещением окружности постоянного или переменного радиуса, называются:

ГЧО поверхности включает: образующую прямую т и ось вращения і. Если milj, образуется поверхность

К коникам НЕ относится

Для однозначного задания поверхности на чертеже необходимо и достаточно решить вопрос о принадлежности поверхности произвольной

Проекции каркаса могут быть построены, если задан

К коникам НЕ относится

К линейчатым поверхностям НЕ относится

Поверхность, образованная непрерывной совокупностью замкнутых плоских сечений, определенным образом ориентированных в пространстве, носит название

В процессе образования поверхности образующая НЕ может

Определитель поверхности — это

Набор гесметрическик фигур и алгоритм их взаимодействия

Вращательно поступательным перемещением точки

Плоскость, перпендикулярная оси вращения, пересекает поверхность по

Поверхность, образованная непрерывной совокупностью последовательных положений некоторой линии, перемещающейся в пространстве, носит название

Циклическая поверхность с образующей постоянного вида называется

К линейчатым поверхностям не относятся

Двуполостный гиперболоид вращения

Плоскость, проходящая через ось вращения, пересекает поверхность по

Поверхность, полученная вращением эллипса вокруг малой оси, называется

Поверхность, образованная движением прямой т, параллельной плоскости параллелизма по двум направляющим кривым линиям, называется

В НГ классификация поверхностей производится на основании

Формы образующей и закона образования

Коноид — поверкность, образованная движением прямолинейной образующей, параллельной плоскости

Двум направляющим, кривой и прямой

ГЧО поверхности включает: образующую прямую т и ось вращенияj. Если m.lj. образуется поверхность

ГЧО поверхности включает: образующую прямую т и ось вращения j. Если m скрещивается с j. Образуется поверхность

Геликоиды — это винтовые поверхности, образующими которых являются

ГЧО поверхности включает: образующую прямую и ось вращения j. Если mnj, образуется поверхность

Образующая циклической поверхности может быть

Образующая винтовой поверхности может быть

Прямой или кривой
Проекционный метод

1. Только для параллельного проецирования действительно одно из перечисленных утверждений, а именно:
   1. Отношение отрезков прямой равно отношению их проекций.
2. Только для параллельного проецирования действительно одно из перечисленных утверждений, а именно:
   1. Проекции параллельных прямых параллельны.
3. Свойства оригинала, не искажающиеся при проецировании, носят название:
   1. Инварианты.
4. Не является инвариантом проецирования следующее утверждение:
   1. Прямой угол всегда проецируется без искажения.
5. Без исключения операция центр. проецирования осуществляться:
   1. Может в проективном пространстве.
6. Свойство чертежа передавать достоверную информацию об оригинале, которая позволяет восстановить форму оригинала и его положение в пространстве, носит название:
   1. 3. Обратимости.
7. Свойство чертежа вызывать пространственное представление об оригинале носит название:
   1. 4. Наглядности.
8. Чертеж, на котором построены или имеется возможность построить две проекции оригинала, носит название:
   1. 2. Полного.
9. Чертеж, на котором имеются средства для восстановления метрики пространства оригинала, носит название:
   1. 3. Метрически определенного.
10. Методы центрального (ЦП) и параллельного (ПП) проецирования в проективном пространстве находятся в следующей логической связке:
    1. пп частный случай цп
11. Масштаб уклона плоскости – это градуированная проекция:
    1. линии наибольшего ската плоскости
12. схема получения проекционного чертежа ортогональными проецированием на две взаимно перпендикулярное плоскости проекции при внешней параметризации оригинала носит название
    1. эпюр Монжа

Числовые отметки

1. Заложение прямой, соответствующее единице превышения, носит название
   1. Уклон
2. Длина горизонтальной проекции отрезка прямой носит название
   1. Заложение
3. На чертеже с числовыми отметками о положении изображенного объекта по высоте позволяет судить
   1. Наличие числовых отметок
4. На чертеже с числовыми отметками стрелкой, острие которой направленно от точек, имеющих большие отметки к точкам, имеющим меньшие отметки, указывается
   1. Направление спуска прямой
5. Разность значений числовых отметок двух точек носит название
   1. Превышение
6. Уклоном прямой называется
   1. Тангенс угла наклона прямой к плоскости проекций
7. Совокупность ортогональной проекции точки на некоторую горизонтальную плоскость с числом, выражающим расстояние от точки до этой плоскости, называется
   1. Проекцией с числовой отметкой
8. Уклон прямой
   1. Обратно пропорционален интервалу прямой
9. Масштаб уклона плоскости — это градуированная проекция
   1. Линии наибольшего ската плоскости
10. На чертеже с числовыми отметками заданы точки А, В, С, D. Выше плоскости нулевого уровня расположена(-ы) точка(-и)
    1. АиВ
11. На чертеже с числовыми отметками заданы точки А. В. С, D. Ниже плоскости нулевого уровня расположена(-ы) точка
    1. C

начертательная геометрия

1. Изображение, являющееся носителем геометрической информации об оригинале, является его:
   1. Геометрической моделью.
2. Предметом начертательной геометрии НЕ является разработка:
   1. Методов исследования оригиналов по их уравнениям.
3. Начертательная геометрия – это раздел геометрии, в котором объекты окружающего мира исследуются с помощью:
   1. Чертежей.
4. Дисциплина «Начертательная геометрия» относится к группе дисциплин:
   1. Изучающих научную аргументацию основ будущей профессии.
5. Основоположником начертательной геометрии как науки, является:
   1. Гаспер Монж.
6. Дисциплины, изучаемые студентами в вузе, относится
   1. К любой из названных групп
7. Объекты окружающего мира в рамках НГ принято называть
   1. Оригиналами
8. Дальше других точек от фронтальной плоскости проекции находится
   1. Точка В
9. Ближе других точек к горизонтальной плоскость проекции находится
   1. Точка Д
10. Дальше других точек от профильной плоскости проекции находится
    1. Точка А

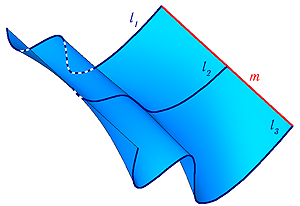
Способы преобразования проекций применяются для решения:

Способы преобразования проекций применяются с целью нахождения:

Истинных величин фигур и рациональных способов решения задач.

Оригинал остается неподвижным относительно исходных плоскостей проекций при использовании способа:

Замены плоскостей проекций.

Оригинал остается неподвижным относительно исходных плоскостей проекций при использовании способа:

Оригинал изменяет свое положение относительно исходных плоскостей проекций при использовании способа:

Вращения вокруг линии уровня.

Оригинал изменяет свое положение относительно исходных плоскостей проекций при использовании способа:

2. Плоскопараллельного перемещения.

При использовании способа замены плоскостей проекций новая плоскость проекций по отношению к незаменяемой плоскости проекций располагается:

При использовании способа замены плоскостей проекций расстояние от новой оси до новой проекции точки:

Равно расстоянию от заменяемой оси до заменяемой проекции точки.

К четырем основным задачам на преобразование можно отнести:

3. Обе названные задачи.

К четырем основным задачам на преобразование можно отнести:

3. Обе названные задачи.

Плоскопараллельным называется перемещение, при котором все точки оригинала перемещаются:

Параллельно плоскости проекций.

Плоскопараллельное перемещение возможно относительно:

Любой из плоскостей проекций.

Траектория движения каждой точки оригинала при плоскопараллельном перемещении относительно горизонтальной плоскости проекций находится:

В горизонтальной плоскости.

Траектория движения каждой точки оригинала при плоскопараллельном перемещении относительно фронтальной плоскости проекций находится:

Во фронтальной плоскости.

При плоскопараллельном перемещении относительно горизонтальной плоскости проекций остается равной самой себе, изменяя лишь свое положение:

Горизонтальная проекция оригинала.

При плоскопараллельном перемещении относительно фронтальной плоскости проекций остается равной самой себе, изменяя лишь свое положение:

Фронтальная проекция оригинала.

Частным случаем плоскопараллельного перемещения является способ:

Плоскость вращения точки относительно оси вращения расположена:

При вращении вокруг фронтально-проецирующей оси траектория точки проецируется в виде окружности на:

Фронтальную плоскость проекций.

В начертательной геометрии задачи на определение взаимного положения оригиналов носят название:

В начертательной геометрии задачи на определение истинных величин фигур носят название:

Способы преобразования проекций НЕ применяются для:

Определения видимости элементов фигур.

Для преобразования плоскости общего положения в плоскость уровня способом ЗПП требуется:

Для преобразования плоскости общего положения в проецирующую плоскость способом ЗПП требуется:

Для преобразования плоскости общего положения в проецирующую плоскость способом ППП требуется:

Для преобразования плоскости общего положения в плоскость уровня способом ППП требуется:

Для преобразования прямой общего положения в проецирующую прямую способом ЗПП требуется:

Для преобразования прямой общего положения в проецирующую прямую способом ППП требуется:

Для преобразования прямой общего положения в прямую уровня способом ППП требуется:

Для преобразования прямой общего положения в прямую уровня способом ЗПП требуется:

Тени, получаемые на неосвещенной поверхности фигуры, называются:

Действительной тенью точки на плоскость проекций является:

след светового луча на первой, встретившейся на его пути, плоскости проекций

При стандартном освещении тень горизонтального отрезка на горизонтальной плоскости проекций:

параллельна самому отрезку

Преобразовать плоскость общего положения в горизонтальной плоскость уровня одним поворотом можно используя способ

вращения вокруг горизонтали

Для того что бы преобразовать общего положения в горизонтальную плоскость уровня одним поворотом ось вращения должна является

Горизонтальная линия уровня

По отношению к незаменяемой плоскости новая плоскость проекции располагается

Расстояние от новой оси до новой проекции точки

Равно расстоянию от заменяемой оси до заменяемой проекции точки

Видео:Лекция 5. Поверхности вращения. часть 1.Скачать

Лекция 7. Поверхности

Видео:ПоверхностиСкачать

7.1. Поверхности. Образование и задание поверхности на чертеже

Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с проектированием, конструированием и изготовлением различных поверхностей. Большинство задач прикладной геометрии сводится к автоматизации проектно-конструкторского процесса и воспроизведения сложных поверхностей. Способы формообразования и отображения поверхностей составляют основу инструментальной базы трехмерного моделирования современных систем автоматизированного проектирования.

Рассматривая поверхности как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0, можно выделить алгебраические поверхности (F(x,y,z)— многочлен n-ой степени и трансцендентные (F(x,y,z)— трансцендентная функция.

Если алгебраическая поверхность описывается уравнением n-й степени, то поверхность считается поверхностью n-го порядка. Произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет исследуемая поверхность. Порядок поверхности может быть определен также числом точек её пересечения с произвольной прямой, не принадлежащей целиком поверхности, считая все точки (действительные и мнимые).

Поверхность можно рассматривать, как совокупность последовательных положений l₁,l₂… линии l перемещающейся в пространстве по определенному закону (Рисунок 7.1). В процессе образования поверхности линия l может оставаться неизменной или менять свою форму — изгибаться или деформироваться. Для наглядности изображения поверхности на эпюре Монжа закон перемещения линии l целесообразно задавать графически в виде одной линии или целого семейства линий (m, n, p…).

Подвижную линию принято называть образующей (l_i), неподвижные – направляющими (m). Такой способ образования поверхности принято называть кинематическим .

Примером такого способа могут служить все технологические процессы обработки металлов режущей кромкой, когда поверхность изделия несёт на себе «отпечаток» режущей кромки резца, т.е. её поверхность можно рассматривать как множество линий конгруэнтных профилю резца.

Рисунок 7.1 — Кинематическая поверхность

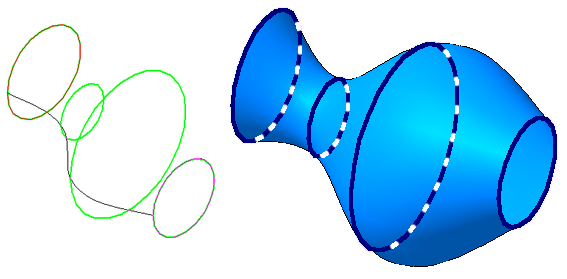
По виду образующей различают поверхности линейчатые и нелинейчатые , образующая первых – прямая линия, вторых – кривая.

Линейчатые поверхности в свою очередь разделяют на развертывающиеся , которые можно без складок и разрывов развернуть на плоскость и неразвертывающиеся .

Значительный класс поверхностей формируется движением окружности постоянного или переменного радиуса. Такие поверхности носят название циклические (Рисунок 7.2).

Рисунок 7.2 — Циклическая поверхность

Если группировать поверхности по закону движения образующей линии, то большинство встречающихся в технике поверхностей можно разделить на:

• поверхности вращения;
• винтовые поверхности;
• поверхности с плоскостью параллелизма;
• поверхности параллельного переноса.

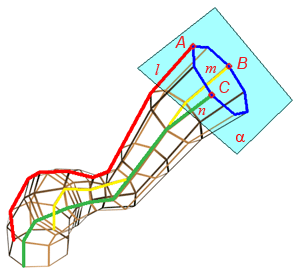
Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).

Для графического изображения поверхности на чертеже используется её каркас.

Множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества, называется каркасом поверхности .

Поверхность может быть задана и конечным множеством точек, которое принято называть точечным каркасом .

Проекции каркаса могут быть построены, если задан определитель поверхности – совокупность условий, задающих поверхность в пространстве и на чертеже.

Различают две части определителя: геометрическую и алгоритмическую.

Геометрическая часть определителя представляет собой набор постоянных геометрических элементов (точек, прямых, плоскостей и т.п.), которые могут и не входить в состав поверхности.

Вторая часть – алгоритмическая (описательная) – содержит перечень операций, позволяющий реализовать переход от фигуры постоянных элементов к непрерывному каркасу.

Например, циклическая поверхность, каркас которой состоит из восьмиугольников (Рисунок 7.3), может быть задан следующим образом:

• Геометрическая часть определителя: три направляющих l, m, n.

• Алгоритмическая часть: выбираем плоскость α; находим точки А, В, С, в которых α пересекает соответственно направляющие l, m, n. Строим восьмиугольник, определяемый тремя найденными точками. Переходим к следующей плоскости и повторяем построение

Рисунок 7.3 –Образование циклической поверхности

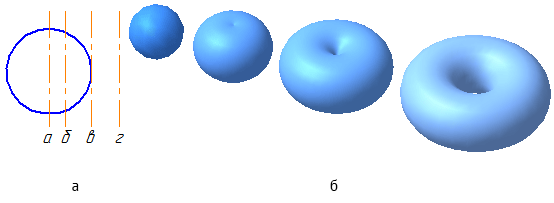
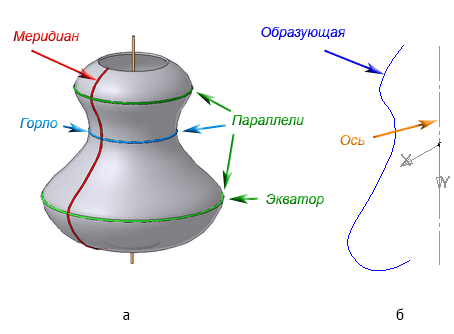
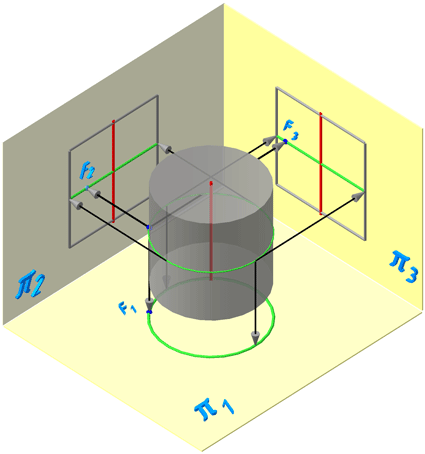
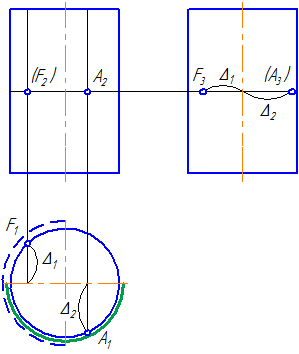
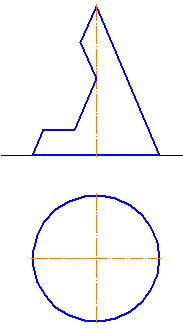
Видео:Лекция 5.Поверхности вращения. Часть 5.Скачать

7.2. Поверхности вращения

Поверхностями вращения называются поверхности, полученные вращением образующей вокруг неподвижной оси (Рисунок 7.5).

Цилиндрическая и коническая поверхности бесконечны (т.к. бесконечны образующие); сферическая, торовая поверхности — конечны.

Сферическая поверхность – частный случай торовой поверхности. При вращении окружности вокруг осей б, в, г (Рисунок 7.4, а) получим торовую поверхность (Рисунок 7.4, б), а вокруг оси а – сферическую.

Рисунок 7.4 – Образование поверхностей вращения

Рисунок 7.5 – Элементы поверхности вращения

Каждая точка образующей линии при вращении вокруг оси описывает окружность, которая располагается в плоскости, перпендикулярной оси вращения. Эти окружности называются параллелями (Рисунок 7.5).

Наименьшая параллель называется горлом , наибольшая – экватором .

Линия пересечения поверхности вращения плоскостью, проходящей через ось, называется меридианом .

Линия пересечения поверхности вращения плоскостью, проходящая через ось, параллельно фронтальной плоскости проекций, называется главным меридианом .

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

7.3. Цилиндрическая поверхность

Цилиндрическая поверхность образуется движением прямой линии, которая в любом своём положении параллельна данному направлению и пересекает криволинейную направляющую (Рисунок 7.6).

Цилиндр – геометрическое тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими все образующие данной поверхности.

Взаимно параллельные плоские фигуры, ограниченные цилиндрической поверхностью, называются основаниями цилиндра .

Если нормальное сечение (плоскость сечения перпендикулярна образующим) имеет форму окружности, то цилиндрическая поверхность называется круговой .

Если образующие цилиндрической поверхности перпендикулярны к основаниям, то цилиндр называется прямым, в противном случае – наклонным .

Рассмотрим проецирование прямого кругового цилиндра и принадлежащей ему точки F.

Условимся, что фронтальная проекция точки F – невидима (Рисунок 7.6).

Рисунок 7.6 – Проецирование цилиндра на плоскости проекций

Горизонтальная и профильная проекции точки F будут видимы.

При определении видимости, образующие, которые находятся на части, обращённой к наблюдателю и обозначенной на π₁ сплошной зелёной линией – на плоскости проекции π₂ видны, а которые находятся на части, обозначенной толстой штриховой линией – видны на π₃.

Пусть точка А на π₂ видима (Рисунок 7.7). Тогда на π₁ она будет видима, а на π₃ невидима.

Рисунок 7.7 – Эпюр прямого кругового цилиндра и принадлежащих ему точек

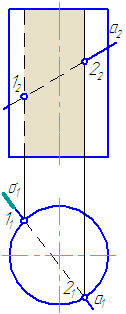
Видео:Лекция VI-2. Устойчивость откосов и склоновСкачать

7.4. Пересечение прямой с поверхностью прямого кругового цилиндра

Для построения точек пересечения прямой линии с поверхностью прямого кругового цилиндра не требуется дополнительных построений. На горизонтальной плоскости проекций точки пересечения (1 и 2) находятся сразу. Фронтальные проекции строим по линиям связи.

Но в общем случае, алгоритм решения рассмотрим на следующем упражнении.

Рисунок 7.8 – Пересечение прямой с поверхностью прямого кругового цилиндра

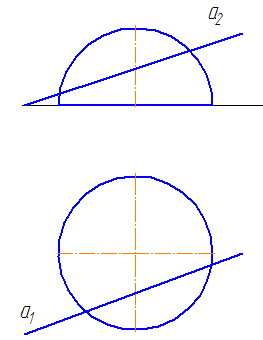
Видео:Лекция 6. Метрические задачиСкачать

Упражнение

Заданы: прямой круговой цилиндр с осью вращения, перпендикулярной плоскости проекций π₁ и прямая а общего положения (Рисунок 7.8).

Построить точки пересечения прямой а с поверхностью цилиндра.

Для построения точек пересечения прямой с поверхностью цилиндра необходимо:

1. Заключить прямую во вспомогательную секущую плоскость частного положения σ (горизонтально-проецирующую).
2. Построить фигуру пересечения поверхности цилиндра горизонтально-проецирующей плоскостью: результат пересечения — четырехугольник (на π₂ условно заштрихован).
3. Найти точки «входа» и «выхода» прямой: на пересечении её фронтальной проекции с фронтальными проекциями сторон четырёхугольника (они же — проекции образующей цилиндра);

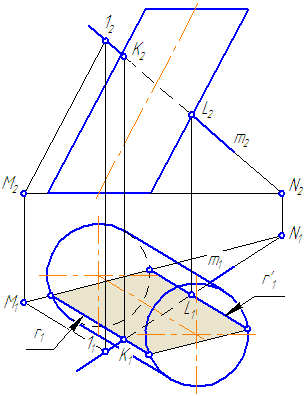
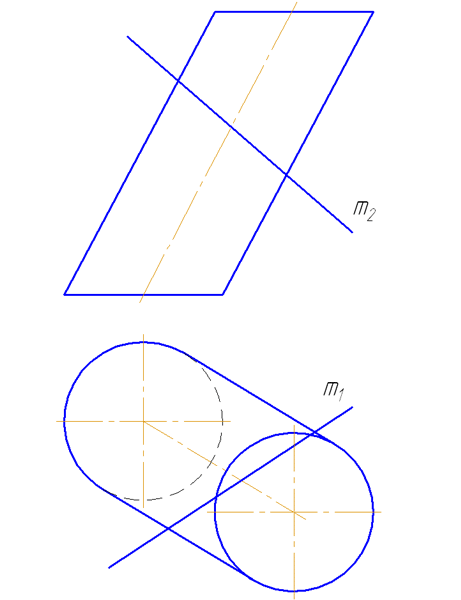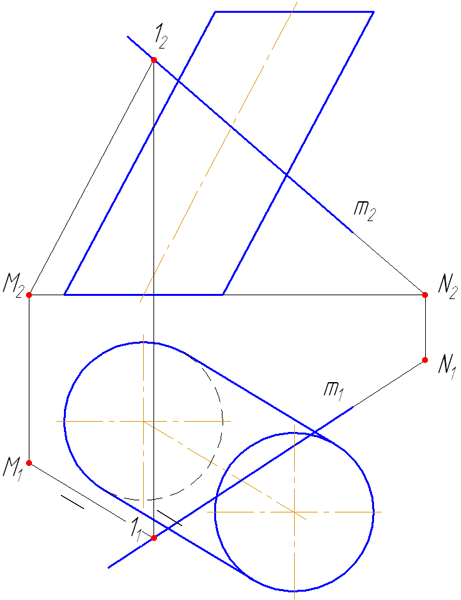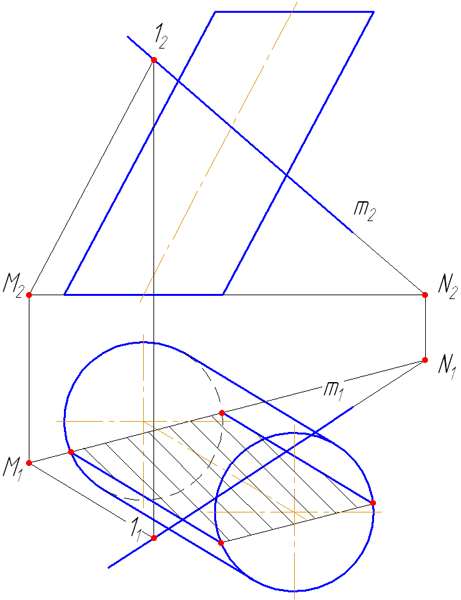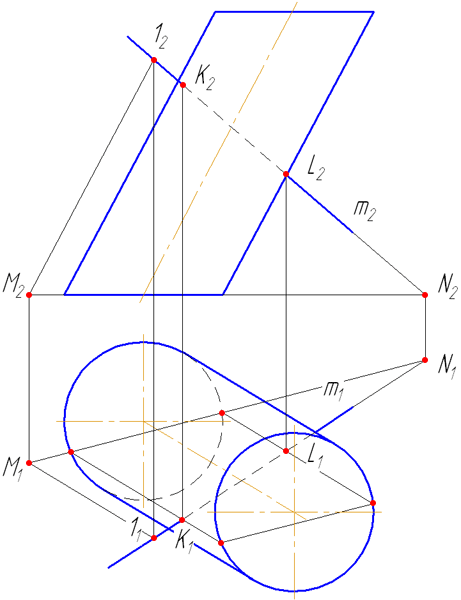
Прямая а пересекается со сторонами сечения в двух точках – 1 и 2.

Определим видимость участков прямой: очевидно, что между точками 1-2 прямая невидима, а на плоскости проекций π₂ будет ещё невидим участок прямой от точки 1 до левой крайней образующей.

Видео:Пересечение линии и поверхностиСкачать

7.5. Пересечение прямой с поверхностью наклонного цилиндра

Видео:Образование поверхностей перемещением кривых, 1973Скачать

Упражнение

Заданы : наклонный круговой цилиндр с осью вращения, наклонной к плоскости проекций π₁ и прямая mобщего положения (Рисунок 7.9).

Построить точки пересечения прямой mс поверхностью цилиндра.
Решение :

Для построения точек пересечения прямой с поверхностью цилиндра необходимо:

Рисунок 7.9 – Пересечение прямой с наклонным цилиндром

1. Заключить прямую m во вспомогательную плоскость σ, дающую в сечении наиболее простую фигуру – четырехугольник (σ параллельна оси цилиндра или образующим). Эту плоскость зададим двумя пересекающимися прямыми m∩(1M);
2. Построить горизонтальный след плоскости σ (прямую пересечения σ с плоскостью проекций π₁) как проходящую через горизонтальные следы прямых m и (1M) (точки пересечения прямых с плоскостью проекций π₁ (основания)) – (MN);
3. Найти точки пересечения MN с окружностью основания цилиндра. Через эти точки провести образующие r, по которым плоскость σ пересекает боковую поверхность цилиндра:

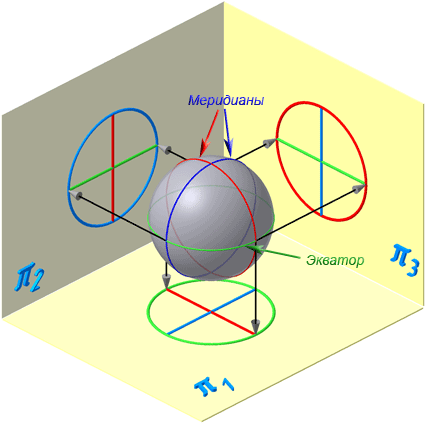
На анимации ниже представлена последовательность построения точек пересечения прямой с наклонным цилиндром.

Видео:Задачи 4.3.8 и 4.3.9.Скачать

7.6. Сферическая поверхность

Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.

Шаром называется тело, ограниченное сферической поверхностью.

Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).

Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.

Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.

Рисунок 7.10 – Проецирование сферической поверхности

Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой .

Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек

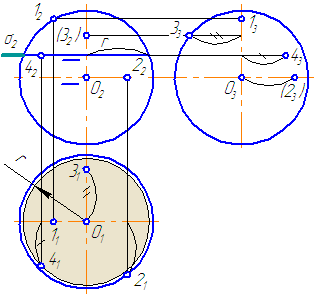
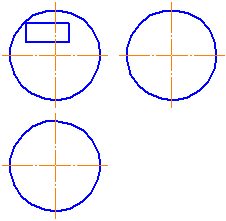
Видео:Начертательная геометрия (задача 4-10). Пересечение поверхностей.Скачать

Упражнение

Заданы: сферическая поверхность тремя проекциями (Рисунок 7.11) и фронтальные проекции точек 1, 2, 3, 4.

Необходимо построить горизонтальные и профильные проекции заданных точек.

• Проанализируем их расположение на поверхности сферы. Точки 1, 2, 3 лежат на очерковых образующих сферы.
• Точка 1 принадлежит главному меридиану (очерковой окружности на π₂), проекция которого на π₁ совпадает с проекцией горизонтальной оси, на π₃ – с проекцией вертикальной оси.
• Недостающие проекции точки 1 находим посредством линий проекционной связи. Все проекции точки 1 видимы.
• Рассмотрим положение точки 2. Точка 2 принадлежит экватору (очерковой окружности на π₁), проекции которого на π₂ и π₃ совпадают с проекцией горизонтальной оси. Горизонтальная проекция точки 2 строится посредством линии проекционной связи, для построения профильной проекции необходимо измерить расстояние, отмеченное дугой, и отложить его по линии связи от точки О₃ вправо. Профильная проекция точки 2 невидима.
• Точка 3 принадлежит очерковой окружности на π₃, которая также является меридианом, проекции которого на π₂ и π₁ совпадают с проекцией вертикальной оси. Профильная проекция точки строится посредством линии проекционной связи. Для построения горизонтальной проекции точки 3 необходимо расстояние, отмеченное на π₃ двумя засечками, отложить на π₁ вверх от точки О₁. Горизонтальная и профильная проекции точки 3 видимы.
• Для построения проекций точки 4 необходимо ввести вспомогательную секущую плоскость (зададим плоскость σ//π₁ и σ⊥π₂). Плоскость σ пересекает поверхность сферы по окружности радиусом r. На π₁ строим данное сечение и по линии проекционной связи находим 4₁. Для построения профильной проекции необходимо расстояние, отмеченное засечкой, отложить по линии проекционной связи на π₃ вправо от оси. Все проекции точки 4 видимы.

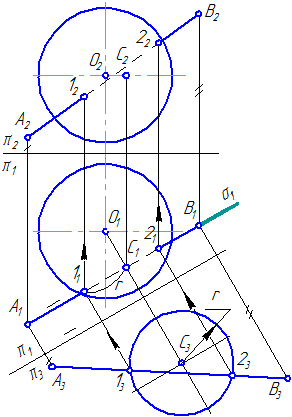
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

7.7. Пересечение прямой с поверхностью сферы

Видео:Лекция 9. Гранные поверхностиСкачать

Упражнение

Заданы: сфера и прямая общего положения АВ.

Найти: точки пересечения прямой с поверхностью сферы (точки «входа» и «выхода»).

Чтобы найти точки пересечения прямой с поверхностью сферы необходимо:

1. Заключить прямую во вспомогательную плоскость, пересекающую поверхность сферы так, чтобы получались простые фигуры (например, круг, ограниченный окружностью);
2. Построить фигуру пересечения сферы вспомогательной плоскостью;
3. Найти общие точки прямой и контура фигуры (окружность): так как прямая и окружность лежат в одной плоскости, то они, пересекаясь, образуют точки, общие для прямой и сферы, которые и будут являться искомыми точками (Рисунок 7.12).

• Через прямую проводим плоскость σ. Пусть σ⊥π₁ и пересекает сферу по окружности радиусом r. С – центр окружности сечения ОС⊥σ:

Рисунок 7.12 – Пересечение прямой с поверхностью сферы

• Введём π₃⊥π₁ и π₃//σ₁. Построим проекцию окружности сечения на π₃ и проекцию А₃В₃.
• Находим точки их пересечения 1₂ и 2₃.
• Определим видимость участков прямой.
• На π₁ точки 1 и 2 находятся на переднем полушарии, следовательно, на π₂ они видимы.

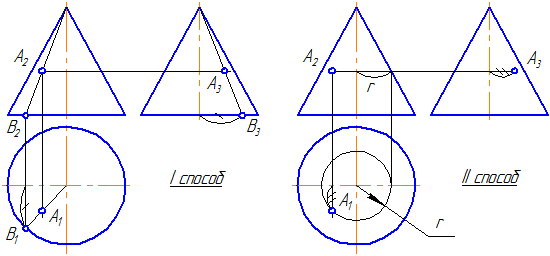
Видео:Начертательная геометрия Лекция №8 ( 2 часть ) Пересечение поверхностейСкачать

7.8. Коническая поверхность

Коническая поверхность образуется движением прямой линии (образующей), которая в любом своем положении проходит через неподвижную точку и пересекает криволинейную направляющую (имеет две полости).

Тело, ограниченное замкнутой конической поверхностью вершиной и плоскостью, называется конусом .

Плоская фигура, ограниченная конической поверхностью, называется основанием конуса .

Часть конической поверхности, ограниченная вершиной и основанием, называется боковой поверхностью конуса .

Если основание конуса является кругом, то конус называется круговым .

Если вершина конуса расположена на перпендикуляре к основанию, восстановленному из его центра, то конус называется прямым круговым .

Рисунок 7.13 – Принадлежность точки конической поверхности

Рассмотрим вопрос принадлежности точки А поверхности конуса.
Дана фронтальная проекция точки А и она видима (Рисунок 7.13).

1 способ . Для построения ортогональных проекций точки, расположенной на поверхности конуса, построим проекции образующей, проходящей через данную точку. При таком положении точки А все её проекции – видимы.

2 способ . Точка А лежит на параллели конуса радиусом r. На π₁ строим проекцию окружности (параллели) и по линии проекционной связи находим А₁. По двум проекциям точки строим третью.

Видео:Начертательная геометрия задача 3-1Скачать

7.9. Пересечение прямой с поверхностью конуса

Пусть задан прямой круговой конус и прямая общего положения m (Рисунок 7.14). Найти точки «входа» и «выхода» прямой с поверхностью конуса.

1. Через прямую m проводим вспомогательную секущую плоскость σ, дающую в сечении наиболее простую фигуру.
2. Применение в качестве вспомогательной секущей плоскости проецирующей плоскости в данном случае нецелесообразно, так как в сечении получится кривая второго порядка, которую нужно строить по точкам.

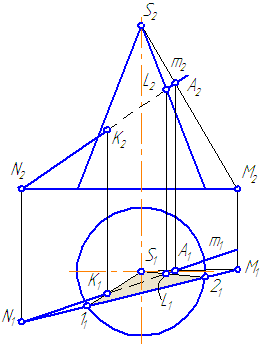
Наиболее простая фигура – треугольник. Для этого секущая плоскость σ должна пройти через вершину S. Плоскость зададим с помощью двух пересекающихся прямых σ=SM∩MN или, что, то же самое, (σ=SM∩m).

1. Возьмем на прямой m точку А и соединим её с вершиной. Прямая SA пересечёт плоскость основания в точке М.
2. Построим горизонтальные проекции этих объектов.
3. Продлим фронтальную проекцию прямой m до пересечения с плоскостью основания в точке N.

Рисунок 7.14 – Построение точек пересечения прямой с поверхностью конуса

1. Построим её горизонтальную проекцию.
2. Соединим точки M₁N₁, на пересечении с окружностью основания получим точки 1 и 2.
3. Строим треугольник сечения конуса плоскостью σ, соединив точки 1 и 2 с вершиной S.
4. На пересечении образующих 1-S и 2-S с прямой m получим искомые точки K и L.
5. Определим видимость прямой относительно поверхности конуса.

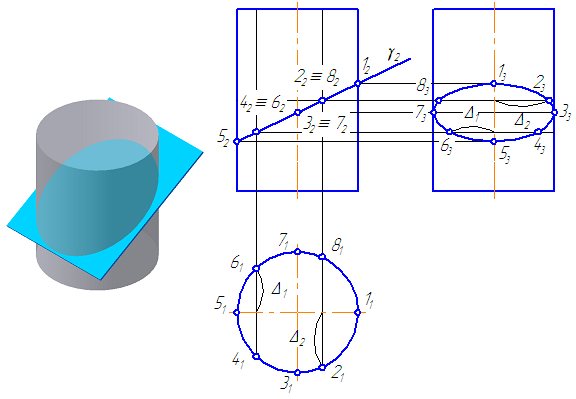
На анимации ниже представлена последовательность построения точек пересечения прямой с поверхностью конуса.

Видео:Начертательная геометрия (задача 4-5) Пересечение поверхностейСкачать

7.10. Пересечение цилиндра плоскостью

Пусть плоскость сечения γ – фронтально-проецирующая (Рисунок 7.15).

1. Если плоскость сечения γ параллельна оси цилиндра, то она пересекает цилиндр по четырехугольнику.
2. Если плоскость сечения γ перпендикулярна оси цилиндра, то она пересекает цилиндр по окружности.
3. Если плоскость сечения γ не параллельна и не перпендикулярна оси цилиндра в сечении эллипс.

Рассмотрим алгоритм построения сечения – эллипс (Рисунок 7.15):

Рисунок 7.15 – пересечение цилиндра плоскостью

1. Находим и строим характерные точки (точки, не требующие дополнительных построений) – в нашем случае, точки принадлежащие крайним образующим – 1, 3, 5, 7. Одновременно с этим, данные точки определяют величину большой и малой оси эллипса.
2. Для построения участка эллипса необходимо построить не менее 5-ти точек (так как лекальная кривая второго порядка определяется как минимум пятью точками). Для построения точек 2, 4, 6, 8 возьмем на π₁ произвольно расположенные образующие цилиндра, которые проецируются на данную плоскость проекции в точки.
3. Построим вторые проекции данных образующих. Из точек пересечения вторых проекций образующих с проекцией плоскости сечения γ проводим линии связи к π₃. Для построения третьей проекции, например, точки 6 измеряем расстояние Δ₁ и откладываем его по соответствующей линии связи на π₃. Симметрично ей, относительно оси вращения, строим точку 4. Аналогично строятся другие точки.

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

7.11. Пересечение сферы плоскостью

Плоскость пересекает поверхность сферы всегда по окружности. Задачу пересечения плоскости со сферой мы рассматривали при решении задачи построения точек пересечения прямой с поверхностью сферы (см. выше).

Видео:Лекция 11. Винтовые поверхностиСкачать

7.12. Пересечение конуса плоскостью

Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π₂ (Рисунок 7.16).

1. Если плоскость проходит через вершину (1) – в сечении две образующие и прямая пересечения с плоскостью основания.
2. Если плоскость перпендикулярна оси вращения конуса (2) – в сечении окружность.
3. Если плоскость не параллельна ни одной образующей (пересекает все образующие (3)) – в сечении эллипс.
4. Если плоскость параллельна одной образующей конуса – в сечении парабола (на примере – плоскость сечения (4) параллельна крайней образующей конуса).
5. Если плоскость параллельна двум образующим (пересекает обе полости конической поверхности (5)) – в сечении гипербола (рисунок 7.17).

Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса

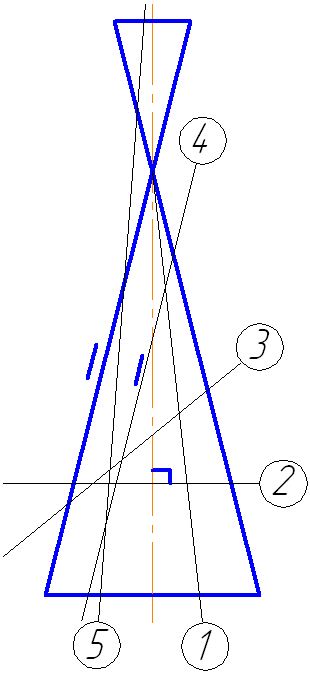
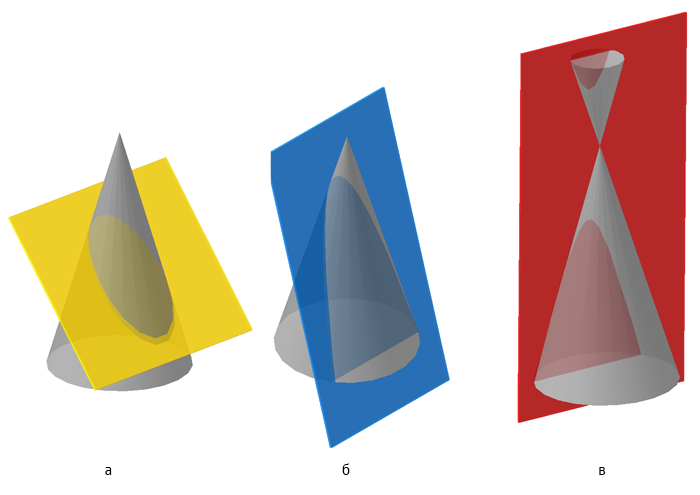
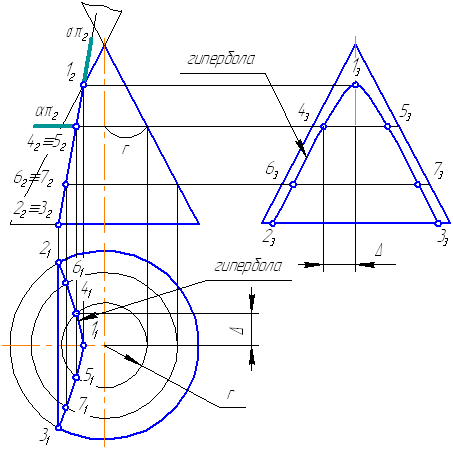
Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.

Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)

Рассмотрим пример построения сечения конической поверхности плоскостью.

Рисунок 7.19 – Построение пересечения конической поверхности плоскостью

Пусть задана секущая проецирующая плоскость σ⊥π₂ (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.

1. Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.
2. Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π₂ и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π₁. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π₁ и π₃ совпадают с линиями проекционной связи.
3. На пересечении этих двух сечений на плоскости проекций π₁ строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.
4. Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.
5. Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.

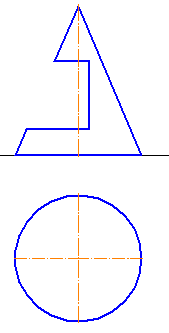
На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.

Видео:Пересечение поверхностей. Построение линии пересечения.Скачать

7.13. Задачи для самостоятельной работы

1. Достроить проекции сферы с заданным вырезом (Рисунок 7.20).

Рисунок 7.20
2-3. Построить три проекции конуса с призматическим отверстием (Рисунки 7.21, 7.22).

Рисунок 7.21

Рисунок 7.22
4. Построить точки «входа» и «выхода» прямой при пересечении её с поверхностью полусферы (Рисунок 7.23).

Рисунок 7.23

📸 Видео

Пересечение поверхностей призмы и полусферы. Пошаговое видео. Инженерная графикаСкачать