Постройте сумму и разность векторов изображенных на рисунке

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a + b = <a_x + b_x; a_y + b_y> » data-order=» a + b = <a_x + b_x; a_y + b_y> » style=»min-width:55.0847%; width:55.0847%;»> a + b = <a_x + b_x; a_y + b_y>Для трехмерных задач

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a + b = <a_x + b_x; a_y + b_y; a_z + b_z> » data-order=» a + b = <a_x + b_x; a_y + b_y; a_z + b_z> «> a + b = <a_x + b_x; a_y + b_y; a_z + b_z>Для n-мерных векторов

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a + b = <a₁ + b₁; a₂ + b₂; . a_n + b_n> » data-order=» a + b = <a₁ + b₁; a₂ + b₂; . a_n + b_n> «> a + b = <a₁ + b₁; a₂ + b₂; . a_n + b_n>

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: ( a + b ) + c = a + ( b + c )

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (- a ) = 0

Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.

Видео:Сложение векторов. 9 класс.Скачать

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:

Формула вычитания векторов

Элементы вектора c равны попарной разности соответствующих элементов a и b .

<table data-id="251" data-view-id="251_83403" data-title="Формулы вычитания векторов" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a — b = <a_x — b_x; a_y — b_y> » data-order=» a — b = <a_x — b_x; a_y — b_y> » style=»min-width:55.0847%; width:55.0847%;»> a — b = <a_x — b_x; a_y — b_y>Для трехмерных задач

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a — b = <a_x — b_x; a_y — b_y; a_z — b_z> » data-order=» a — b = <a_x — b_x; a_y — b_y; a_z — b_z> «> a — b = <a_x — b_x; a_y — b_y; a_z — b_z>Для n-мерных векторов

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a — b = <a₁ — b₁; a₂ — b₂; . a_n — b_n> » data-order=» a — b = <a₁ — b₁; a₂ — b₂; . a_n — b_n> «> a — b = <a₁ — b₁; a₂ — b₂; . a_n — b_n>

Видео:Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Примеры задач

Задание 1
Вычислим сумму векторов и .

Задание 2
Найдем разность векторов и .

Видео:8 класс, 43 урок, Сумма двух векторовСкачать

Сложение и вычитание векторов.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Сложение и вычитание векторов.

Сумма двух векторов. Законы сложения векторов. Правило параллелограмма.

Представим себе такую ситуацию. Направляясь из школы домой, вам захотелось пить и вы решили зайти сначала в магазин, а затем уже домой. Цель достигнута: вы из школы добрались домой. Сейчас мы описали принцип первого правила сложения векторов.

Чтобы найти вектор суммы двух векторов и , нужно:

совместить параллельным переносом начало вектора с концом вектора ;

провести вектор из начала вектора в конец вектора ;

получившийся вектор и есть вектор суммы: .

Если к вектору прибавить нулевой вектор по правилу треугольника, то получим вектор , т.е. справедливо равенство: .

Утверждение. Если и – произвольные точки, то .

Сложение векторов подчиняется алгебраическим законам.

ТЕОРЕМА. Для любых векторов и справедливы равенства:

Доказательство теоремы в случае, когда векторы коллинеарны достаточно простое. Его вы можете провести самостоятельно. Мы рассмотрим случай, когда данные векторы неколлинеарны.

1). Отметим произвольную точку и отложим от этой точки вектор . Воспользуемся правилом треугольника и прибавим к нему вектор . Вектором суммы этих двух векторов является вектор . (Рисунок слева).

Теперь от точки и отложим вектор . По правилу треугольника прибавим к нему вектор . Вектором суммы этих двух векторов является вектор . (Рисунок справа).

– параллелограмм и точка совпадает с точкой . Значит, , т.е.

2). От точки отложим вектор , от точки отложим вектор , а от точки – вектор . Найдём суммы векторов по правилу треугольника.

При доказательстве первой формулы получился параллелограмм, причём, из точки выходят два вектора и , а вектор их суммы является диагональю параллелограмма. На основе этого возникает второе правило геометрического сложения векторов.

Чтобы найти вектор суммы двух векторов и , нужно:

совместить параллельным переносом начала векторов и ;

на этих векторах достроить параллелограмм;

вектором суммы является вектор, который лежит на диагонали параллелограмма, имеющий своё начало в начале исходных векторов.

Сумма нескольких векторов.

Сложение нескольких векторов происходит по принципу правила треугольника. Складываются два вектора, к вектору суммы прибавляется следующий вектор и т.д. Приведём пример.

Отметим точку и отложим от неё вектор . Прибавим к нему вектор по правилу треугольника. . Теперь к вектору прибавим вектор . . К вектору прибавляем вектор . . Осталось к вектору прибавить вектор . .

Итак, . Значит, суммой векторов является вектор, с началом в начале первого вектора и концом – в конце последнего. Такое сложение векторов называется правилом многоугольника.

Чтобы найти вектор суммы нескольких векторов, нужно:

последовательно совместить параллельным переносом начало последующего вектора с концом предыдущего;

вектором суммы всех векторов является вектор, с началом в начале первого вектора и концом – в конце последнего.

Определение. Разностью двух векторов и называется такой вектор , что при сложении его с вектором получается вектор .

Вычитание векторов можно производить, руководствуясь двумя понятиями: следствием из правила треугольника сложения векторов; определением разности двух чисел. Разберём каждое из них.

Сложим векторы и по правилу треугольника. По рисунку видно, что . Отсюда, и . Значит, разность двух векторов можно составить, совмещая их начала, либо совмещая их концы. Отсюда два правила:

Чтобы найти вектор разности двух векторов, нужно:

совместить параллельным переносом начала этих векторов;

вектором разности является вектор с началом в конце второго вектора и концом в конце первого вектора.

Чтобы найти вектор разности двух векторов, нужно:

совместить параллельным переносом концы этих векторов;

вектором разности является вектор с началом в начале первого вектора и концом в начале второго вектора.

Далее, из алгебры мы знаем, что для того, чтобы из числа вычесть число , нужно к числу прибавить число, противоположное числу , т.е. . Такое же правило справедливо и для векторов.

ТЕОРЕМА. Для любых векторов справедливо равенство:

1. Найдём разность векторов по I правилу. Вектором разности является вектор (рисунок слева). А теперь найдём сумму векторов по правилу треугольника, где – вектор, противоположный вектору . Вектором суммы является вектор (рисунок справа). Не трудно заметить, что . Они сонаправлены и имеют одинаковые модули.

2. А теперь докажем то же самое аналитически. По определению разности векторов,

Что и требовалось доказать.

Из этой теоремы следует третье правило вычитания векторов.

Чтобы найти вектор разности двух векторов, нужно к первому вектору прибавить вектор, противоположный второму.

Используя это правило вычитания векторов, способ сложения векторов выбирается произвольно.

Вектор является суммой векторов и . Определите, какой из четырёх рисунков верный.

Проведите векторы . Какая геометрическая фигура у вас получилась?

Вектор является разностью векторов и . Определите, какой из четырёх рисунков верный.

Вектор является суммой векторов и . Определите, какой из четырёх рисунков верный.

Выразите вектор через векторы , используя рисунок.

Выразите вектор через векторы , используя рисунок.

Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?

Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?

Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?

Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?

Длина вектора равна , а длина вектора равна . Сколько различных целых значений может принимать длина вектора ?

В квадрате проведены диагонали и . Укажите номера верных утверждений.

– параллелограмм. Найдите сумму векторов .

– прямоугольник. Диагонали и пересекаются в точке . Укажите номера верных утверждений.

параллелограмм. Выразите векторы и через векторы и .

– параллелограмм. Выразите векторы и через векторы и .

– прямоугольник. Выразите векторы и через векторы и .

– параллелограмм. Выразите векторы и через векторы и .

Найдите длины векторов , изображённых на клетчатой бумаге с размерами клетки 1 х 1.

Две стороны прямоугольника равны 20 и 21. Найдите длину суммы векторов и .

Две стороны прямоугольника равны 7 и 24. Найдите длину разности векторов и .

На каждом рисунке найдите длину вектора (размеры клетки 1 х 1).

На каждом рисунке найдите длину суммы векторов и (размеры клетки 1 х 1).

На каждом рисунке найдите длину разности векторов и , изображённых на клетчатой бумаге с размерами клетки 1 х 1.

Краткое описание документа:

Теоретическая часть данной разработки содержит определения, свойства, правила, связанные с геометрическим сложением и вычитанием векторов. К каждому понятию предложен рисунок, разобраны примеры. Практическая часть разработки содержит задания на построение суммы и разности векторов, а также аналитическое определение суммы и разности векторов. Есть задания, встречающиеся на ОГЭ.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 954 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 684 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 67 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Сложение векторов. Правило параллелограмма. 9 класс.Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 504 643 материала в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

§ 2. Сложение и вычитание векторов

Другие материалы

• 16.10.2019
• 806
• 0

• 16.10.2019
• 205
• 0

• 15.10.2019
• 133
• 0

• 15.10.2019
• 151
• 1

• 15.10.2019
• 145
• 2

• 15.10.2019
• 913
• 0

• 20.09.2019
• 211
• 0

• 19.09.2019
• 1224
• 247

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 16.10.2019 4030
• DOCX 370.1 кбайт
• 72 скачивания
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Колесник Марина Анатольевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 3 года и 10 месяцев
• Подписчики: 0
• Всего просмотров: 260830
• Всего материалов: 132

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Умножение вектора на число. 9 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили создать в школах «ящики доверия» для обращений к психологу

Время чтения: 1 минута

В Рособрнадзоре видят предпосылки к снижению качества знаний у школьников на фоне пандемии

Время чтения: 1 минута

Минпросвещения намерено решить вопрос с третьей сменой в школах в 2023 году

Время чтения: 1 минута

Все школы Ненецкого АО перевели на удаленку

Время чтения: 1 минута

Санкт-Петербургский госуниверситет переходит на дистанционное обучение

Время чтения: 1 минута

Школы Пскова перевели на дистанционное обучение

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📸 Видео

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

сложение ВЕКТОРОВ вычитание ВЕКТОРОВ 9 класс геометрия АтанасянСкачать

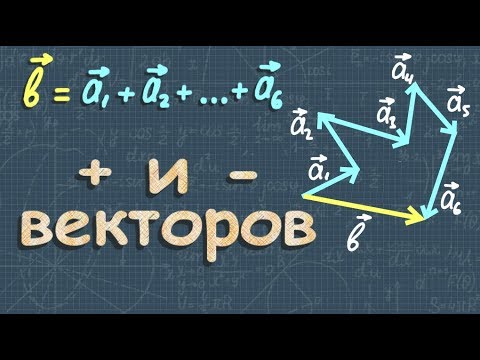
Сложение и вычитание векторов практикумСкачать

Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

10 класс, 40 урок, Сложение и вычитание векторовСкачать

10 класс, 41 урок, Сумма нескольких векторовСкачать

Геометрия 9 класс (Урок№3 - Вычитание векторов)Скачать

Координаты вектора. 9 класс.Скачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать