- Глава 5. Окружность Ответы к параграфу 5.1 Окружность и прямая
- Задание № 408
- Задание № 409
- Задание № 410
- Задание № 411
- Задание № 412
- Задание № 413
- Задание № 414
- Задание № 415
- Задание № 416
- Задание № 417
- Задание № 418
- практические работы по наглядной геометрии методическая разработка по геометрии (5 класс) на тему
- Скачать:
- Предварительный просмотр:
- Расстояние между прямыми в пространстве онлайн
- Предупреждение
- Расстояние между прямыми в пространстве − теория, примеры и решения
- 1. Расстояние между параллельными прямыми в пространстве
- 2. Расстояние между скрещивающимися прямыми в пространстве
- 🔍 Видео
Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Глава 5. Окружность
Ответы к параграфу 5.1 Окружность и прямая
Задание № 408
Что можно сказать о взаимном расположении прямой и окружности, если расстояние от центра окружности до прямой равно 4 см, а радиус окружности равен:
а) 3 см;
б) 4 см;
в) 6 см?
Подсказка. Сделайте схематический рисунок.
а) Прямая и окружность не имеют общих точек.
б) Прямая и окружность касаются друг друга.
в) Прямая и окружность пересекаются.
Задание № 409
Начертите произвольную окружность и отметьте на ней точку A. Постройте касательную к окружности в точке A.
Задание № 410
К окружности, радиус которой равен 6 см, проведены две параллельные касательные (рис. 5.3). Чему равно расстояние между ними?
6 + 6 = 12 (см) − расстояние между касательными.
Ответ: 12 см.
Задание № 411
Начертите две параллельные прямые. Постройте какую−нибудь окружность, для которой эти прямые являются касательными. Сколько таких окружностей можно построить? Где лежат их центры?
Окружностей можно построить множество. Центры этих окружностей лежат на прямой, параллельной данным и равноудаленной от них.
Задание № 412
Прямая k и окружность пересекается в точках A и B. Прямая k перемещается к центру окружности параллельно самой себе. В какой момент длина отрезка AB будет наибольшей? Сделайте соответствующий рисунок.
Длина отрезка AB будет наибольшей, когда прямая k проходит через центр окружности. В этом случае отрезок AB будет являться диаметром окружности.
Задание № 413
Проведите прямую и постройте какую−нибудь окружность радиусом 3 см, для которой эта прямая являются касательной. Сколько таких окружностей можно построить? Где расположены их центры?
Можно построить бесконечное множество таких окружностей. Их центры будут лежать по обе стороны от данной прямой на прямых, параллельных данной, на расстоянии, равному радиусу окружности 3 см.
Задание № 414
Проведите прямую и отметьте на ней произвольную точку M. Постройте несколько окружностей разных радиусов, касающихся данной прямой в точке M. Где лежат центры всех таких окружностей?
Центры окружностей лежат на прямой, перпендикулярной данной прямой.
Задание № 415
Начертите в тетради квадрат со стороной 8 см. Постройте окружность, касающуюся всех сторон квадрата.
Задание № 416
Представьте данное число в виде произведения двух десятичных дробей (укажите два решения):
а) 0,12;
б) 0,064;
в) 0,0002;
г) 0,3.
б) 0,064 = 0,4 * 0,16 = 0,8 * 0,08
в) 0,0002 = 0,1 * 0,002 = 0,001 * 0,2
Задание № 417
Найдите значение каждого из выражений:
1) 25 − 3,6 * 1,5 + 2,5;
2) (25 − 3,6) * (1,5 + 2,5);
3) 25 − 3,6 * (1,5 + 2,5).
Задание № 418
1) В полиэтиленовый пакет, выдерживающий 5 кг, положили 1,8 кг огурцов, а яблок в 1,5 раза больше. Не порвется ли пакет?
2) Представьте, что вы хотите помочь бабушке подготовить материал для изготовления шерстяного ковра из ниток разного цвета. Чтобы получить нужный узор, 1/10 всех ниток должна быть красного цвета, 2/5 − синего, 3/20 − коричневого, остальные − белого. У бабушки имеется 700 г ниток белого цвета. Рассчитайте, сколько граммов ниток каждого цвета надо взять для выполнения работы.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

практические работы по наглядной геометрии
методическая разработка по геометрии (5 класс) на тему
Практические работы по наглядной геометрии для 5-6 классов
Видео:Параллельные прямые. 6 класс.Скачать

Скачать:
| Вложение | Размер |
|---|---|
| naglyadnaya_geometriya.docx | 115.4 КБ |
| prakt_po_naglyadnoy_geom.docx | 171.6 КБ |
Бесплатный марафон подготовки к ЕГЭ на зимних каникулах
Учи.Дома запускает бесплатный марафон в котором каждый день. В течении 5 дней утром ты будешь получать одно задание по выбранному предмету, а вечером его решение. Твоя задача, успеть выполнение задание до того как получишь ответ.
Бесплатно, онлайн, подготовка к ЕГЭ
Видео:Перпендикулярные прямые. 6 класс.Скачать

Предварительный просмотр:
Практическая работа № 1
«Окружность»
(выполняется на нелинованной бумаге)
Отметьте точки А и В . Проведите окружность с центром в точке А , проходящую через точку В . Выполните следующие задания:
1. Измерьте и запишите, чему равен радиус окружности.
2. Проведите диаметр окружности и обозначьте его.
3. Постройте окружность с центром в точке В радиусом 4 см.
Практическая работа № 2
«Ломаная»
(выполняется на нелинованной бумаге)
Начертите ломаную из трех звеньев, обозначьте ее. Выполните следующие задания:
1. Измерьте и запишите длину каждого звена ломаной.
2. Вычислите длину ломаной.
3. Постройте отрезок, длина которого равна длине ломаной.
Практическая работа № 3
«Углы»
(выполняется на нелинованной бумаге)
Выполните следующие задания:
1. Постройте угол АОВ , равный 40°.
2. Проведите луч ОС так, чтобы угол АОС был прямым, угол СОВ — тупым.
3. Проведите луч ОK — биссектрису угла СОВ .
4. Вычислите величину угла KОА .
Практическая работа № 4
«Прямоугольники»
(выполняется на нелинованной бумаге)
Начертите прямоугольник и обозначьте его. Выполните следующие задания:
1. Измерьте и запишите длины сторон прямоугольника.
2. Вычислите периметр прямоугольника.
3. Проведите одну из диагоналей прямоугольника. Измерьте длину диагонали и сравните ее с длиной большей стороны прямоугольника.
4. Измерьте угол между диагональю и большей стороной прямоугольника. Запишите величину этого угла.
Практическая работа № 5
«Треугольники»
(выполняется на нелинованной бумаге)
Начертите равнобедренный треугольник и обозначьте его. Выполните следующие задания:
1. Измерьте и запишите величины углов треугольника.
2. Запишите, каким является ваш треугольник: прямоугольным, остроугольным или тупоугольным.
3. Выполните необходимые измерения и найдите периметр треугольника.
Практическая работа № 6
«Площади»
(выполняется на клетчатой бумаге)
Постройте прямоугольник со сторонами 5 см и 4 см. Выполните следующие задания:
1. Разбейте прямоугольник на квадраты со стороной 1 см. Заштрихуйте какой-нибудь квадрат, площадь которого равна 1 см 2 .
2. Вычислите площадь прямоугольника.
3. Начертите еще один прямоугольник, одна сторона которого равна 10 см, а площадь равна площади первого прямоугольника.
Практическая работа № 7
«Многогранники»
(выполняется на клетчатой бумаге)
Возьмите модель многогранника и выполните следующие задания:
1. Определите число вершин многогранника.
2. Поставьте многогранник на лист бумаги и обведите нижнюю грань. Начертите таким же образом все его грани. Укажите равные грани (соедините их линиями).
3. Подсчитайте и запишите, сколько у данного многогранника ребер.
Практическая работа № 8
«Прямоугольный параллелепипед»
(выполняется на клетчатой бумаге)
Рассмотрите рисунок и выполните задания:
1. Выпишите все невидимые грани параллелепипеда.
2. Известны длины ребер: АВ = 3 см, АD = 6 см, AK = 4 см. Запишите длины ребер MN, NL, DL .
3. Начертите грань АВМK в натуральную величину.
Практическая работа № 1
«Пересекающиеся прямые»
(выполняется на нелинованной бумаге)
Проведите прямую а . На прямой а отметьте точку В. Отметьте точку С , не лежащую на прямой а . Выполните следующие задания:
1. Проведите через точку С прямую, перпендикулярную прямой а .
2. Проведите через точку В прямую с , пересекающую прямую а под углом 30°.
3. Надпишите величины трех других углов между прямыми а и с .
Практическая работа № 2
«Параллельные прямые»
(выполняется на клетчатой бумаге)
Скопируйте рисунок и выполните следующие задания:
1. Укажите на вашем рисунке величины углов, образовавшихся при пересечении прямых с и b .
2. Проведите какую-нибудь прямую, параллельную прямой с .
Практическая работа № 3
«Расстояние»
(выполняется на нелинованной бумаге)
Проведите прямую а и отметьте точку В , не лежащую на этой прямой. Выполните следующие задания:
1. Определите расстояние от точки В до прямой а .
2. Проведите прямую с , параллельную прямой а . Найдите расстояние между прямыми а и с .
Практическая работа № 4
«Окружности»
(выполняется на нелинованной бумаге)
Отметьте точки А и В , расстояние между которыми равно 5 см. Выполните следующие задания:
1. Постройте окружность с центром в точке А радиусом 2 см.
2. Проведите окружность с центром в точке В , пересекающую первую окружность. Измерьте и запишите, чему равен ее радиус.
3. Постройте две окружности с центром в точке В , касающиеся первой окружности. Запишите, чему равны их радиусы.
Практическая работа № 5
«Осевая симметрия»
(выполняется на нелинованной бумаге)
Проведите прямую k и отметьте точки А, В и С, не лежащие на этой прямой. Выполните следующие задания:
1. Постройте точки, симметричные точкам А, В и С относительно прямой k . Обозначьте их.
2. Запишите пары точек, симметричных относительно прямой k .
3. Начертите окружность с центром в точке А , проходящую через точку В . Постройте окружность, симметричную ей относительно прямой k .
Практическая работа № 6
«Треугольник»
(выполняется на нелинованной бумаге)
Постройте равнобедренный треугольник, если его боковые стороны равны 5 см, а угол между ними равен 40°. Вычислите величины двух других углов построенного треугольника.
Практическая работа № 7
«Параллелограмм»
(выполняется на нелинованной бумаге)
Постройте какой-нибудь параллелограмм, стороны которого равны 3 см и 5 см. Обозначьте его АВСD . Выполните следующие задания:
1. Запишите длину каждой стороны параллелограмма. Вычислите его периметр.
2. Измерьте и запишите величину угла СDА . Укажите равный ему угол параллелограмма.
3. Постройте центр симметрии параллелограмма и обозначьте его буквой О .
Практическая работа № 8
«Призма»
(выполняется на клетчатой бумаге)
Скопируйте пятиугольную призму и выполните следующие задания:
1. Закрасьте основания призмы.
2. Выпишите видимые боковые ребра призмы.
3. Длины ребер оснований призмы равны 10 см, боковые ребра — 15 см. Найдите длину проволоки, необходимой для изготовления каркаса призмы.
Устные упражнения на развитие воображения
Упражнение «Пять предметов» . Представьте пять предметов меньше вашего мизинца (колпачок ручки, горошина и т.д.). Представьте пять предметов больше автобуса (кит, поезд и т.п.). Представьте пять предметов, имеющих форму шара.
Упражнение «Анализ чертежа». Рассмотрите чертеж. Из каких фигур он состоит? Каково их взаимное расположение? Мысленно уберите с чертежа одну из фигур, «верните» ее назад. Проделайте это для остальных фигур. Как можно построить такой чертеж? В каком порядке будут появляться фигуры на вашем чертеже? Предложите несколько вариантов построения.
Упражнение «Зрительный след». Если, посмотрев на некий объект, вы закроете глаза, то его образ автоматически сохранится в вашей памяти еще на какое-то время. Постарайтесь соединить зрительную память с вашим мысленным представлением. Например, посмотрите на развертку куба, закройте глаза и рассмотрите картинку, сохраненную в памяти. Когда образ потускнеет, откройте глаза, посмотрите на развертку, снова закройте глаза и снова посмотрите на ее образ в вашей памяти. Повторите это несколько раз в удобном для вас темпе, пока хотя бы на секунду не вырисуется четкая картина. После этого постарайтесь уже сознательно воспроизвести мысленный образ развертки. А теперь усложним задачу: аналогично предыдущему, будем рассматривать процесс сворачивания развертки и воспроизводить его по памяти.
Упражнение «Геометрические тела». Представьте куб. Не старайтесь сразу же создать образ: вначале подробно изучите взаимное расположение граней, ребер, вершин. Мысленно манипулируя кубом, рассмотрите его со всех сторон, в том числе и изнутри. Постарайтесь получить ощущение объемности. Проделайте это с параллелепипедом, призмой, пирамидой, додекаэдром, октаэдром, икосаэдром. Выполните аналогичное задание для сферы и шара.
Упражнение «Фигуры вращения». Представьте себе, что проволочная модель прямоугольника вращается вокруг одной из его сторон. Пусть скорость вращения сначала небольшая, а затем увеличьте скорость вращения. Какую фигуру опишет прямоугольник? Выполните это упражнение для прямоугольного треугольника, вращающегося вокруг одного из катетов, вокруг гипотенузы; окружности, вращающейся вокруг диаметра; ромба, вращающегося вокруг оси симметрии.
Упражнение «Образы идей». Вообразите себе идею симметрии. Это определенный образ чего-то симметричного, или вы способны создать абстрактный образ Симметрии, не представляя себе ничего конкретного? Много ли в нем деталей? Проделайте это с идеями: равенства, параллельности, перпендикулярности, пересечения, измерения.
Исследования и эксперименты
«Угол с вершиной на окружности». Постройте окружность и проведите ее диаметр АВ . Постройте угол АСВ с вершиной С , лежащей на окружности. Каким: острым, прямым или тупым, является этот угол? Постройте и измерьте еще два угла с вершинами на окружности, «опирающиеся» на диаметр. Какой вывод можно сделать?
«Сколько диагоналей у многоугольника» . Число диагоналей многоугольника можно подсчитать так: 1) найти число диагоналей, выходящих из одной вершины, — их на 3 меньше, чем вершин (начертите семиугольник и проведите все диагонали из одной вершины); 2) умножить это число на число вершин; 3) разделить результат на 2 (объясните, почему). Сколько диагоналей у семиугольника? стоугольника? У какого многоугольника 9 диагоналей?
«Какие многогранники могут получиться при разрезании куба плоскостью» . Вылепите куб из пластилина и, выбирая разные направления, разрежьте его на две части. Нарисуйте куб и покажите для каждого случая, как проходит по кубу линия разреза.
«Пересекающиеся прямые» . Изобразите все случаи взаимного расположения трех прямых на плоскости (их 4). Какое наибольшее число точек пересечения могут иметь три прямые? четыре прямые? пять прямых?
«Сумма углов треугольника» . Начертите на листе бумаги 5–6 различных треугольников. Измерьте величины углов каждого треугольника. Для каждого треугольника найдите сумму его углов. Выскажите предположение о сумме углов любого треугольника.
«Сколько осей симметрии у правильных многоугольников». Сколько осей симметрии у правильного треугольника? четырехугольника? пятиугольника? десятиугольника? Нарисуйте эти фигуры от руки и проведите их оси симметрии. Сколько осей симметрии у правильного стоугольника? девяностодевятиугольника? Запишите выражение для вычисления числа осей симметрии правильного n -угольника.
Задания прикладного характера
1. Изготовьте все развертки куба (их 11).
2.Сделайте развертки правильных многогранников и склейте эти модели.
3. Вылепите из пластилина: куб, шар, цилиндр, конус, треугольную пирамиду, треугольную призму.
4. Выполните необходимые измерения и вычислите площадь: классной комнаты, школьного здания, школьной территории.
5. Выполнив необходимые измерения, найдите расстояние от своего места в классе до окна, доски, двери, ближайшей стены.
Темы проектных работ
1. План школьной территории
2. Этот симметричный мир
3. Геометрия города будущего
4. Как измеряли наши предки
5. Правильные многогранники в природе и творениях человека
6. Геометрия на клетчатой бумаге
Контроль учебных достижений
В отличие от арифметического, геометрический материал не так существенно связан с формированием и отработкой опорных умений, составляющих базу и основу для дальнейшего продвижения по курсу, поэтому было бы неверно проводить контроль за его усвоением так же жестко. Здесь целесообразно после изучения законченного блока взаимосвязанных вопросов проводить тематические проверочные работы, например — в форме теста. За их выполнение выставляется обычная отметка. Учитель может выставлять отметки по своему усмотрению, принимая во внимание все педагогические функции отметки, учитывая и индивидуальные особенности учащихся, и особенности выполнения конкретных заданий, и характер изучаемой темы. Примеры таких тематических тестов приводятся ниже.
Предлагаемые тесты направлены на проверку владения основным понятийным аппаратом по конкретной теме. Чтобы проверка носила комплексный характер, она должна содержать и проверку владения практическими навыками построения фигур и выполнения измерений. Для этого тесты могут быть дополнены заданиями практического характера, можно воспользоваться практическими работами, приведенными выше, или их аналогами. Таким образом, тест будет состоять из двух частей: теоретической и практической.
Для итоговой проверки и оценки усвоения материала по наиболее важным вопросам в конце изучения курса также можно воспользоваться тестом. Такая форма проверки позволяет охватить большой объем материала и может содержать задания как теоретического, так и практического характера. Это может стать хорошим мониторингом готовности к изучению систематического курса геометрии, предстоящего будущим семиклассникам.
Итоговый тест, приведенный в конце лекции, состоит из двух частей. Часть 1 содержит задания, проверяющие владение учащимися основными понятиями курса, умение «читать» геометрический чертеж, часть 2 — задания, проверяющие владение практическими навыками построения геометрических фигур и конфигураций.
В части 1 представлены задания с двумя типами ответов: с выбором ответа, где учащийся должен выбрать один верный, на его взгляд, вариант ответа из трех предложенных, и с кратким ответом, когда учащийся должен записать полученный им в ходе решения задачи ответ в отведенную для этого строку. Все необходимые вычисления могут выполняться устно или на черновике. Во всех заданиях, связанных с вычислением геометрических величин, при записи ответа учащийся должен указать единицы измерения, при этом перевода одних единиц в другие не требуется, но если единицы указаны неправильно или дано только числовое значение, то выполнение этого задания не может быть засчитано как верное.
Практическая часть работы выполняется на отдельном листе нелинованной бумаги. Построения должны быть выполнены с помощью чертежных инструментов (если не оговорено отдельно) точно, аккуратно, тонко заточенным карандашом. При этом никаких обоснований или дополнительных объяснений построений, а также записи с использованием символов от учащихся не требуется. На чертеже должны оставаться все вспомогательные линии, которые необходимо провести в ходе выполнения построений. Это дает учителю возможность проанализировать степень овладения алгоритмом построения. Если необходимые при построении линии на чертеже отсутствуют, это свидетельствует о том, что оно, скорее всего, подгонялось, выполнялось на глаз, выполнение задания засчитано быть не может.
Каждое верно выполненное задание и первой, и второй частей оценивается одним баллом; при этом задания 11 и 14 состоят из двух подзаданий, за выполнение каждого из которых выставляется 1 балл. Таким образом, максимальное число баллов, которое может быть получено за выполнение теста, равно 16. Можно предложить такую систему оценивания: ученик получает отметку «5», если он набрал 14 и более баллов, отметку «4», если набрал не менее 11 баллов, отметку «3» — не менее 8 баллов.
1. Математика: Контрольные работы для 5– 6 кл. общеобр. учреждений / Л.В. Кузнецова и др. — М.: Просвещение, 2005.
2. Математика: учеб. для 5 кл. / Под ред. Г.В. Дорофеева, И.Ф. Шарыгина. — М.: Просвещение, 2008.
3. Математика: учеб. для 6 кл. / Под ред. Г.В. Дорофеева, И.Ф. Шарыгина. — М.: Просвещение, 2008.
1. Не выполняя измерений, для каждого отрезка укажите его длину.
А. ______________________________________________
Б. ______________________________________________
В.______________________________________________
Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Расстояние между прямыми в пространстве онлайн
С помощю этого онлайн калькулятора можно найти расстояние между прямыми в пространстве. Дается подробное решение с пояснениями. Для вычисления расстояния между прямыми в пространстве, задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:6 класс. Урок 3. Пересекающиеся и параллельные прямые: теорияСкачать

Расстояние между прямыми в пространстве − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
 . . | (1) |
 , , | (2) |
Прямые (1) и (2) в пространстве могут совпадать, быть паралленьными, пересекаться, или быть скрещивающимся. Если прямые в пространстве пересекаются или совпадают, то расстояние между ними равно нулю. Мы рассмотрим два случая. Первый − прямые параллельны, и второй − прямые скрещиваются. Остальные являются частыми случаями. Если при вычислении расстояния между параллельными прямыми мы получим расстояние равным нулю, то это значит, что эти прямые совпадают. Если же расстояние между скрещивающимися прямыми равно нулю, то эти прямые пересекаются.
1. Расстояние между параллельными прямыми в пространстве
Рассмотрим два метода вычисления расстояния между прямыми.
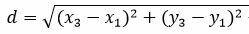  |
которое и является расстоянием между прямыми L1 и L2 (Рис.1).
 |
Пример 1. Найти расстояние между прямыми L1 и L2:
 | (3) |
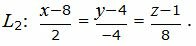 | (4) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Найдем проекцию точки M1 на прямую L2. Для этого построим плоскость α, проходящей через точку M1 и перпендикулярной прямойL2.
Для того, чтобы плоскость α было перепендикулярна прямой L2, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L2, т.е. в качестве нормального вектора плоскости α можно взять направляющий вектор прямой L2. Тогда уравнение искомой плоскости, проходящей через точку M1(x1, y1, z1) имеет следующий вид:
| m2<x−x1)+p2(y−y1)+ l2(z−z1)=0 | (5) |
| 2(x−1)−4(y−2)+ 8(z−1)=0 |
После упрощения получим уравнение плоскости, проходящей через точку M1 и перпендикулярной прямой L2:
| 2x−4y+ 8z−2=0 | (6) |
Найдем точку пересечения прямой L2 и плоскости α, для этого построим параметрическое уравнение прямой L2.
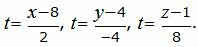 |
Выразив переменные x, y, z через параметр t, получим параметрическое уравнение прямой L2:
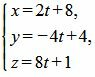 | (7) |
Чтобы найти точку пересечения прямой L2 и плоскости α, подставим значения переменных x, y, z из (7) в (6):
 |
Решив уравнение получим:
 | (8) |
Подставляя полученное значение t в (7), получим точку пересеченияпрямой L2 и плоскости α:
 |
Остается найти расстояние между точками M1 и M3:
 |
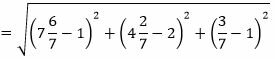  |
Ответ: Расстояние между прямыми L1 и L2 равно d=7.2506.
Метод 2. Найдем расстояние между прямыми L1 и L2 (уравнения (1) и (2)). Во первых, проверяем параллельность прямых L1 и L2. Если направляющие векторы прямых L1 и L2 коллинеарны, т.е. если существует такое число λ, что выполнено равенство q1=λq2, то прямые L1 и L2 параллельны.
Данный метод вычисления расстояния между параллельными векторами основана на понятии векторного произведения векторов. Известно, что норма векторного произведения векторов 
 |
Вычислим координаты вектора 
 |
Вычислим векторное произведение векторов 
 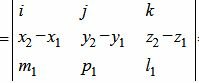 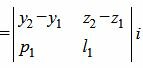  |
Вычисляя определители второго порядка находим координаты вектора c:
Далее находим площадь параллелограмма:
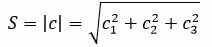 . . |
Расстояние между прямыми L1 и L2 равно:
 , , |
 , , |
Пример 2. Решим пример 1 методом 2. Найти расстояние между прямыми
 | (25) |
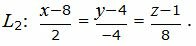 | (26) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Векторы q1 и q2 коллинеарны. Следовательно прямые L1 и L2 параллельны. Для вычисления расстояния между параллельными прямыми воспользуемся векторным произведением векторов.
Построим вектор 
Вычислим векторное произведение векторов 

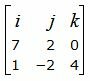 |
Вычислим определитель этой матрицы, разложив ее по первой строке. Результатом этих вычислений получим векторное произведение векторов 
   |
Таким образом, результатом векторного произведения векторов 
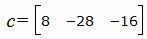 |
Поскольку векторное произведение векторов 
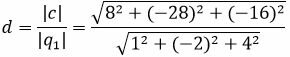  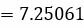 |
Ответ: Расстояние между прямыми L1 и L2 равно d=7.25061.
2. Расстояние между скрещивающимися прямыми в пространстве
Пусть задана декартова прямоугольная симтема координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 (уравнения (1) и (2)).
Пусть прямые L1 и L2 не параллельны (паралельные прямые мы расстотрели в предыдущем параграфе). Чтобы найти расстояние между прямыми L1 и L2 нужно построить параллельные плоскости α1 и α2 так, чтобы прямая L1 лежал на плоскости α1 а прямая L2 − на плоскости α2. Тогда расстояние между прямыми L1 и L2 равно расстоянию между плоскостями L1 и L2 (Рис. 3).
 |
Поскольку плоскость α1, проходит через прямую L1, то он проходит также через M1(x1, y1, z1). Следовательно справедливо следующее равенство:
| A1x1+B1y1+C1z1+D1=0. | (27) |
где n1=<A1, B1, C1> − нормальный вектор плоскости α1. Для того, чтобы плоскость α1 проходила через прямую L1, нормальный вектор n1 должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
| A1m1+B1p1+C1l1=0. | (28) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
| A1m2+B1p2+C1l2=0. | (29) |
Решая систему линейных уравнений (27)−(29), с тремя уравнениями и четыремя неизвестными A1, B1, C1, D1, и подставляя в уравнение
| A1x+B1y+C1z+D1=0. | (30) |
получим уравнение плоскости α1. (Как построить уравнение плоскости, проходящей через прямую, параллельно другой прямой подробно изложено здесь).
Аналогичным образом находим уравнение плоскости α2:
| A2x+B2y+C2z+D2=0. | (31) |
Плоскости α1 и α2 параллельны, следовательно полученные нормальные векторыn1=<A1, B1, C1> и n2=<A2, B2, C2> этих плоскостей коллинеарны. Если эти векторы не равны, то можно умножить (31) на некторое число так, чтобы полученный нормальный вектор n2 совпадал с нормальным вектором уравнения (30).
Тогда расстояние между параллельными плоскостями вычисляется формулой:
 . . |
Полученное расстояние между плоскостями α1 и α2 является также расстоянием между прямыми L1 и L2.
Пример 3. Найти расстояние между прямыми
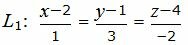 | (32) |
 | (33) |
Построим плоскость α1, проходящую через прямую L1, параллельно прямой L2.
Поскольку плоскость α1 проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(2, 1, 4) и нормальный вектор n1=<m1, p1, l1> плоскости α1 перпендикулярна направляющему вектору q1 прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
| A1x1+B1y1+C1z1+D1=0. | (34) |
а условие параллельности прямой L1 и искомой плоскости α1 представляется следующим условием:
| A1m1+B1p1+C1l1=0. | (35) |
Так как плоскость α1 должна быть параллельной прямой L2, то должна выполнятся условие:
| A1m2+B1p2+C1l2=0. | (36) |
| A1·2+B1·1+C1·4+D1=0. | (37) |
| A1·1+B1·3+C1·(−2)=0. | (38) |
| A1·2+B1·(−3)+C1·7=0. | (39) |
Представим эти уравнения в матричном виде:
 | (40) |
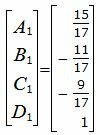 | (41) |
Искомая плоскость может быть представлена формулой:
| A1x+B1y+C1z+D1=0. | (42) |
 |
Упростим уравнение, умножив на число 17.
 | (43) |
Построим плоскость α2, проходящую через прямую L2, параллельно прямой L1.
Поскольку плоскость α2 проходит через прямую L2 , то она проходит также через точку M2(x2, y2, z2)=M2(6, −1, 2) и нормальный вектор n2=<m2, p2, l2> плоскости α2 перпендикулярна направляющему вектору q2 прямой L2. Тогда уравнение плоскости должна удовлетворять условию:
| A2x2+B2y2+C2z2+D2=0. | (44) |
а условие параллельности прямой L2 и искомой плоскости α2 представляется следующим условием:
| A2m2+B2p2+C2l2=0. | (45) |
Так как плоскость α2 должна быть параллельной прямой L1, то должна выполнятся условие:
| A2m1+B2p1+C2l1=0. | (46) |
| A1·6+B1·(−1)+C1·2+D1=0. | (47) |
| A1·2+B1·(−3)+C1·7=0. | (48) |
| A1·1+B1·3+C1·(−2)=0. | (49) |
Представим эти уравнения в матричном виде:
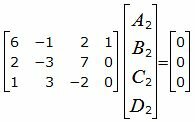 | (50) |
 | (51) |
Искомая плоскость может быть представлена формулой:
| A2x+B2y+C2z+D2=0. | (52) |
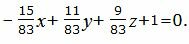 |
Упростим уравнение, умножив на число −83.
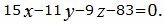 | (53) |
Расстояние между построенными плоскостями (43) и (53) будет расстоянием между прямыми (1) и (2).
Запишем формулы уравнений плоскостей α1 и α2 :
| A1x+B1y+C1z+D1=0. |
| A2x+B2y+C2z+D2=0. |
Поскольку нормальные векторы плоскостей α1 и α2 совпадают, то можно найти расстояние между плоскостями α1 и α2, используя следующую формулу:
 | (54) |
 |
Упростим и решим:
 |
Расстояние между прямыми равно: d=4.839339
🔍 Видео
6 класс. Урок 3. ПРАКТИКА: Пересекающиеся и параллельные прямыеСкачать

Параллельные прямые циркулемСкачать

Пересекающиеся прямые. Математика 6 классСкачать

Параллельные прямые. Математика. 6 класс.Скачать

Перпендикулярные и параллельные прямые. Математика 6 классСкачать

№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Математика это не ИсламСкачать

Параллельные прямые, 6 классСкачать

Перпендикулярные прямыеСкачать

Построение прямой, параллельной даннойСкачать

Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать

Задание №160 - ГДЗ по математике 6 класс (Дорофеев Г.В., Шарыгин И.Ф.)Скачать

Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

6 класс, 44 урок, Параллельные прямыеСкачать

















