Построить треугольник со сторонами

Вы будете перенаправлены на Автор24

Решение задач на построение состоит из четырех основных этапов:

Каждый этап является важным. Например, анализ и исследование задачи необходимы для рассмотрения случаев, когда задача будет иметь решение, а когда – нет.

Построение фигур проще выполнять с помощью транспортира и линейки с делениями, но в математике необходимо уметь выполнять построение, используя циркуль и линейку без делений.

Видео:Строим треугольник по трем сторонам (Задача 5).Скачать

Построение отрезка, равного заданному

Построить отрезок, равный заданному, можно за 3 действия. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить отрезок, который будет равен отрезку $АВ$. Для этого:

1. Отметим произвольно точку $А_1$ и проведем луч с началом в этой точке.
2. С помощью циркуля измерим заданный отрезок $АВ$.
3. Проведем часть окружности с радиусом, равным отрезку $АВ$, и центром в точке $А_1$. В точке пересечения окружности и построенного луча получим точку $В_1$.

Таким образом, построенный отрезок $А_1 В_1$ будет равен заданному отрезку $АВ$.

Видео:Построение треугольника по трём сторонам с помощью циркуля и линейки. 5 классСкачать

Построение угла, равного заданному

Построить угол, равный заданному, можно за $5$ действий. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить угол, который будет равен углу $А$.

1. Отметим произвольную точку $А_1$ и проведем из нее луч $А_1$.
2. Циркулем с произвольным радиусом проведем часть окружности с центром в точке $А$ до пересечения обеих сторон заданного угла $А$.
3. С тем же радиусом проведем часть окружности с центром в точке $А_1$ до пересечения с лучом $А_1$.
4. Из точек пересечения проведем окружности с одинаковым радиусом.
5. Проведем прямую из точки $А_1$ через вторую точку пересечения.

Готовые работы на аналогичную тему

Видео:Построение треугольника по двум сторонам и углу между ними. 7 класс. Геометрия.Скачать

Построение треугольника по двум сторонам и углу между ними

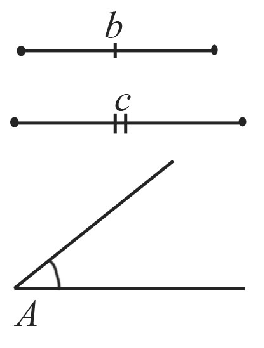
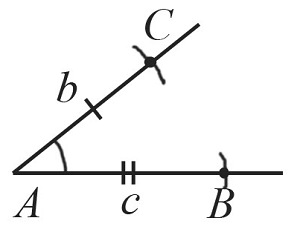
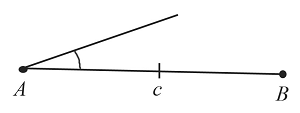
Пусть даны два отрезка $b$ и $с$ и угол $А$:

Необходимо построить треугольник с заданными двумя сторонами и углом между ними:

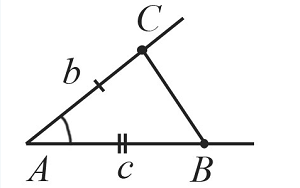
Построение выполняется в 4 этапа, каждый из которых показан на рисунках:

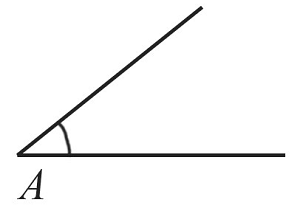
Построим угол $А$, который равен заданному углу по схеме, которая рассматривалась выше.

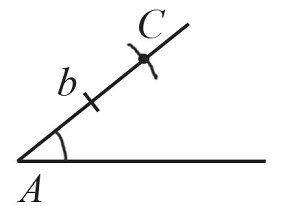
С помощью циркуля замеряем отрезок $b$ и отложим от точки $А$ такой же отрезок на одной из сторон построенного угла. Получим точку $С$.

Циркулем замеряем отрезок $с$ и отложим от точки $А$ такой же отрезок на второй стороне построенного угла. Получим точку $В$.

С помощью линейки соединим точки $В$ и $С$.

Таким образом, получили треугольник $АВС$, построенный по двум сторонам и углу между ними.

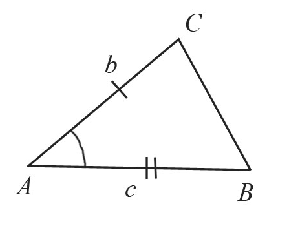
Для облегчения построения полезно схематически изобразить будущий треугольник со всеми необходимыми элементами. Так будет наглядней видно, что после чего нужно строить.

Видео:Построение треугольника по трем сторонам. 7 класс.Скачать

Построение треугольника по стороне и прилегающим к ней углам

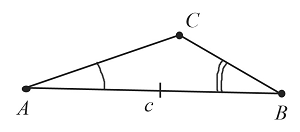
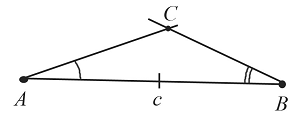
Пусть даны два угла $А$ и $В$ и отрезок $с$:

Необходимо построить треугольник с заданными двумя углами и стороной, к которой они прилегают:

Построение выполняется в $3$ этапа, каждый из которых показан на рисунках:

Начертим произвольный отрезок $АВ$, который равен заданному отрезку $c$.

Построим угол $А$, который равен заданному, как показано выше.

Построим угол $В$, который равен заданному.

Точка пересечения двух сторон построенных углов $А$ и $В$ является вершиной треугольника $С$.

Таким образом, получили треугольник $АВС$, построенный по стороне и двум углам.

Видео:Построение треугольника по стороне и двум прилежащим к ней углам. 7 класс. Геометрия.Скачать

Построение треугольника по трем сторонам

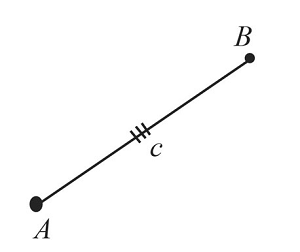
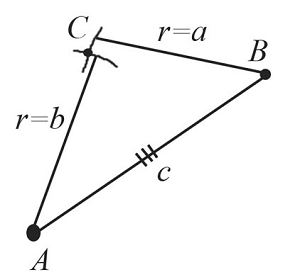
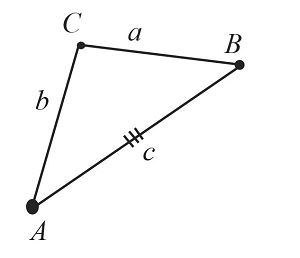
Пусть даны $3$ отрезка $а$, $b$ и $с$.

Необходимо построить треугольник по трем заданным сторонам.

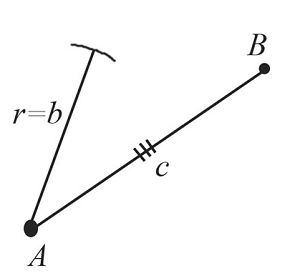
Построим отрезок $АВ$, который равен заданному отрезку $c$.

Из точки $А$ проведем часть окружности с радиусом, равным заданному отрезку $b$.

Из точки $В$ проведем часть окружности с радиусом, равным заданному отрезку $a$. Пересечением обеих окружностей является точка $С$.

Таким образом, получили построенный треугольник $АВС$ по трем заданным сторонам.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 07 2021

Видео:Построить треугольник с заданными сторонами.Скачать

Построение треугольника по трем элементам

Видео:Как построить треугольник по двум сторонам и медиане, проведенной к одной из этих сторонСкачать

Задачи на построение

Широкое распространение в геометрии получили задачи на построение. Суть этих задач состоит в следующем: при заданных начальных условиях нужно построить тот или иной геометрический объект при помощи линейки и циркуля. Разберем общие принципы решения данных задач:

Анализирование задачи. На этом этапе необходимо установить взаимосвязь между заданными условиями и объектом, который нужно изобразить. Результатом выполнения этого этапа является план решения задачи.

Построение. Согласно разработанного плана выполняется построение объекта.

Доказательство. На этом этапе необходимо доказать, что изображенная фигура полностью соответствует заданным условиям.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Изучение. На этом этапе выполняется анализ начальных условий и определение, при каких условиях задача решается одним способом, при каких двумя, а при каких – вовсе не решаема.

Разберем задачи на построение треугольника по трем различным начальным условиям.

Видео:Как построить треугольник по двум сторонам и медиане, проведенной к третьей сторонеСкачать

Изображение треугольника, если задана одна сторона и два прилегающих к ней угла

Задана одна сторон треугольника (BC) и прилежащие к ней углы (∝) и (β) , необходимо построить треугольник.

1. Анализируем условия. Необходимо построить треугольник (ABC) , имея одну сторону (BC) и углы (∠K= ∝ и ∠M= β) к ней прилежащие. Разработаем план решения задачи:

• Начертим прямую a, а на ней отмерим отрезок (BC) ;
• Изображаем угол (∠K= ∝) с центром в вершине (B) на стороне (BC) ;
• Изображаем угол (∠M= β) с центром в вершине (C) на стороне (BC) ;
• На пересечении лучей построенных углов получим точку (A) , соединяем ее с точками (C) и (B) , получаем отрезки (AC) и (AB) .

2. Строим треугольник

3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.

4. Изучение. Заданные углы могут быть построены и в противоположную сторону, соответственно мы можем построить еще один треугольник, но так как он точно такой же, как и первый, можно считать, что решение этой задачи единственное. Учитывая то, что сумма всех углов треугольника должна равняться 180 0 , если сумма углов (∝) и (β) будет равна или больше 180 0 , решения задача не будет иметь.

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Изображение треугольника, если заданы три стороны

Заданы три стороны треугольника (AB) , (AC) и (BC) , нужно построить треугольник.

1. Анализируем условия. Необходимо построить треугольник (ABC) , имея три стороны (AB) , (AC) и BC. Разработаем план решения задачи:

• Начертим прямую (a) , а на ней отмерим отрезок (AB) ;
• Чертим с помощью циркуля две окружности. Одна окружность будет с центром в точке (A) с радиусом (AC) , а вторая с центром в точке (B) с радиусом (BC) ;
• На пересечении окружностей мы получим точку (C) , соединяем ее с точками (A) и (B) , получаем отрезки (AC) и (BC) .

2. Строим треугольник:

3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.

Не нашли что искали?

Просто напиши и мы поможем

4. Изучение. Построенные окружности имеют две точки пересечения, поэтому мы можем построить еще один треугольник, но так как он точно такой же, как и первый, можно считать, что решение этой задачи единственное. Учитывая то, что сумма двух сторон треугольника всегда больше, чем третья его сторона, можно сделать вывод, если это условие не будет выполнено для заданных сторон, то задача не будет иметь решение.

Видео:Построение треугольника по двум сторонам и высоте. Геометрия. 7 класс.Скачать

Изображение треугольника, если заданы две стороны и угол между ними

Заданы две стороны треугольника (AB) и (AC) , а также угол ∝ между ними, необходимо построить треугольник.

1. Анализируем условия. Необходимо построить треугольник (ABC) , имея стороны (AB) и (AC) , а также угол (CAB) , равный (∝) . Разработаем план решения задачи:

• начертим прямую (a) , а на ней отмерим отрезок (AB) ;
• отмеряем угол (MAB) , равный (∝) ;
• откладываем отрезок (AC) на прямой (AM) ;
• чертим третью сторону треугольника (CB) , соединяя точки (B) и (C) .

2. Строим треугольник:

3. Доказательство. По изображенному рисунку делаем вывод, что все заданные условия выполнены в полной мере.

4.Изучение. Прямая a бесконечна, поэтому таких треугольников можно изобразить очень много, но учитывая тот факт, что они все одинаковые, будем считать, что задача имеет одно решение. При условии, если угол (∝) будет равен или больше 180 0 , решения задача не будет иметь, так как сумма всех углов треугольника должна равняться 180 0 .

Видео:Построение треугольника, равного данномуСкачать

Презентация по математике на тему «Построение треугольника по трем сторонам»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Треугольник со сторонами 1, 2 и 4 существует. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Построение треугольника по трем сторонам

В Атлантическом океане есть место, по форме напоминающее геометрическую фигуру, о которой мы сегодня будем говорить. Это место, расположенное между Бермудскими островами, государством Пуэрто-Рико, полуостровом Флорида и называется “бермудским треугольником”. А ещё его называют “дьявольский треугольник”, “треугольник проклятых”. Загадочность его заключается в том, что в нём бесследно исчезают корабли и самолёты. Природа “бермудского треугольника” остаётся тайной и по сей день.

Построение треугольника Построить треугольник АВС со сторонами 5 см, 3 см и 4 см Цель: Научиться строить треугольник по трем сторонам.

Треугольником называется фигура, которая состоит из трёх точек , не лежащих на одной прямой, и трёх отрезков, соединяющих эти точки. В А С Точки А, В и С называются вершинами Отрезки АВ, ВС и СА являются сторонами треугольника Обозначение: АВС

Равносторонний Равнобедренный Разносторонний Виды треугольников

Треугольник – “жесткая” фигура. Если заданы три его стороны, то форму треугольника уже изменить нельзя, не разрушив его. Это свойство широко используется на практике Делая садовую калитку обязательно прибивают планку/доску/, иногда две планки, чтобы получить треугольники. Это придаёт калитке прочность, иначе её перекосит. 2) Стропила зданий имеют вид треугольников. Это придаёт крепость и устойчивость. 3) При строительстве любых мостов в их конструкциях также присутствуют треугольники. Чем больше треугольников в любой конструкции, тем она прочнее.

В различных конструкциях: Телебашня в Токио

Построить треугольник АВС со сторонами 5 см, 3 см и 4 см Строим отрезок АС = 5 см. Строим окружность с центром в точке А и радиусом 3 см. Строим окружность с центром в точке С и радиусом 4 см. Точку пересечения этих окружностей обозначим буквой В – это третья вершина искомого треугольника. Проводим отрезки АВ и ВС. Получили АВС.

Задание Постройте треугольник со сторонами: 1) 3 см, 3 см, 3 см; 2) 4 см, 3 см, 2 см; 3) 5 см, 3 см, 3 см; 4) 6 см, 3 см, 3 см; 5) 8 см, 4 см, 3 см. Примеры № 4 и № 5 показывают, что не всякие три отрезка могут быть сторонами треугольника?

Неравенство треугольника Любая сторона треугольника меньше суммы двух других его сторон

Задание № 434 (1а) Даны три отрезка. Как проверить, можно ли построить треугольник с такими сторонами? Любая сторона треугольника меньше суммы двух других его сторон Или проверить, что наибольший отрезок меньше суммы двух других

Практическая работа 1 ВАРИАНТ 1. В равнобедренном треугольнике одна сторона равна 3,5см, а другая 7,5см. Какая сторона является основанием? Постройте данный треугольник. 2. Сколько различных треугольников можно построить из отрезков длиною 3см, 4 см, 5 см и 7 см? Ответ обоснуйте. 2 ВАРИАНТ 1. В равнобедренном треугольнике одна сторона равна 4 см, а другая 8 см. Какая сторона является основанием? Постройте данный треугольник. 2. Сколько различных треугольников можно построить из отрезков длиною 2 см, 3 см, 5 см и 6 см? Ответ обоснуйте.

Ответы 1 ВАРИАНТ 1. Основание 3,5 см, боковые стороны по 7,5см. 2. Можно построить 3 : 3 см, 4 см, 5 см, т.к. 5

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 942 человека из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 677 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 302 человека из 68 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Строим треугольник по стороне и двум углам (Задача 7).Скачать

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 516 886 материалов в базе

Материал подходит для УМК

«Математика», Бунимович Е.А., Кузнецова Л.В., Минаева С.С. и др.

19. Построение треугольника

Другие материалы

• 08.12.2020
• 93
• 3

• 07.12.2020
• 3461
• 398

• 03.12.2020
• 106
• 2

• 02.12.2020
• 123
• 2

• 02.12.2020
• 359
• 21

• 29.11.2020
• 320
• 15

• 25.11.2020
• 77
• 0

• 24.11.2020
• 99
• 5

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 08.12.2020 732
• PPTX 1.1 мбайт
• 86 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Пушкарева Мария Андреевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 2 года и 1 месяц
• Подписчики: 0
• Всего просмотров: 19078
• Всего материалов: 64

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Построение треугольника по углу и двум сторонам. 7 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

Все школы Оренбурга переводят на дистанционное обучение с 28 января

Время чтения: 1 минута

В школьном курсе мировой истории планируют уделить больше внимания Азии и Африке

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Опубликованы проекты ФГОС по специальностям СПО

Время чтения: 2 минуты

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🔥 Видео

Геометрия - Построение правильного треугольникаСкачать

В треугольнике со сторонами 9 и 6 проведены высоты ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Как построить треугольник по стороне, прилежащему к ней углу и высоте, проведенной к этой сторонеСкачать

Построение треугольника по трем сторонам. 7 класс . Геометрия.Скачать

Как построить треугольник по стороне и двум прилежащим к ней угламСкачать

Как построить треугольник с заданными сторонами.Скачать