Построить сечение тетраэдра по двум точкам и параллельной прямой

Правила построения сечений многогранников:

1) проводим прямые через точки, лежащие в одной плоскости;

2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого

а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);

б) параллельные грани плоскость сечения пересекает по параллельным прямым.

Примеры построения сечений:

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Построим сечение, проходящее через точки M, N, L.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

Найдем прямую пересечения плоскости сечения с плоскостью DD₁C₁C:

пересечем прямую ML (принадлежащую сечению) с ребром DD₁, они лежат в одной плоскости AA₁D₁D, получим точку X₂;

пересечем прямую KN (принадлежащую сечению) с ребром D₁C₁, они лежат в одной плоскости A₁B₁C₁D₁, получим точку X₃;

Точки X₂ и X₃ лежат в плоскости DD₁C₁C. Проведем прямую X₂ X₃ , которая пересечет ребро C₁C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.

MKNTPL — искомое сечение.

Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.

.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

.

Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.

.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

.

Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).

.

Соединим точки P и L ( они лежат в одной плоскости).

.

Видео:Построение сечения параллельно прямойСкачать

Презентация по теме «Построение сечений тетраэдра»

Видео:Как строить сечения тетраэдра и пирамидыСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Построение сечений тетраэдра

Содержание: Актуализация; Изучение нового; Закрепление; Разноуровневая проверочная самостоятельная работа ( 4 варианта) с разбором решения;

* А1 Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.

* А2 Если две точки прямой лежат в плоскости, то и вся прямая лежит в этой плоскости.

* А3 Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. В любой плоскости выполняются аксиомы планиметрии.

АКСИОМЫ СТЕРЕОМЕТРИИ . 1. Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость. 2. Если две точки прямой лежат в плоскости, то и вся прямая лежит в этой плоскости. 3. Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. В любой плоскости выполняются аксиомы планиметрии.

* ОПРЕДЕЛЕНИЯ 1. Две прямые, имеющие только одну общую точку, называются пересекающимися. 2. Две прямые, лежащие в одной плоскости и не имеющие общих точек, называются параллельными. 3 Две прямые, не лежащие в одной плоскости, называются скрещивающимися. 4. Прямая, все точки которой принадлежат плоскости, называется прямой, лежащей в этой плоскости.

* ОПРЕДЕЛЕНИЯ (ПРОДОЛЖЕНИЕ) 5. Прямая пересекает плоскость, если у них есть только одна общая точка. 6. Прямая называется параллельной плоскости, а плоскость- параллельной прямой, если они не имеют общих точек. 7. Прямая называется перпендикулярной плоскости (а плоскость прямой), если прямая перпендикулярна любой прямой, лежащей в этой плоскости.

* ТЕОРЕМЫ 1. Через прямую и не лежащую на ней точку проходит одна и только одна плоскость. 2. Через две пересекающиеся прямые проходит одна и только одна плоскость. 3. Через две параллельные прямые проходит одна и только одна плоскость. 4. Если одна из параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.

Построение сечения тетраэдра через точки M, N, K А B D C N M K

Построение сечения тетраэдра через точки M, N, K А B D C N M K F

Построение сечения тетраэдра через точки M, N, K А B D C N M K L F

Построение сечения тетраэдра через точки M, N, K А B D C N M K L F

А B D C N M K Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а.

А B D C N M K Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а.

А B D C N M K Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K Найдите периметр сечения, если M, N, K – середины ребер и каждое ребро тетраэдра равно а. E

А B D C N M K Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K MN ║ AC E

А B D C N M Е Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K K Р

А B D C N M Е Объясните, как построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K K Р

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C Построите сечение через точки

А B D C N M Q Построите сечение тетраэдра DABC плоскостью, проходящей через возможные точки K Р R

А B D C L M Q Построите сечение тетраэдра DABC плоскостью, проходящей через возможные точки K Р R

А B D C N M Построите сечение тетраэдра DABC плоскостью, проходящей через возможные точки

Самостоятельная работа Вариант 1 Вариант 2 Вариант 3 Вариант 4 Задание 1 Задание 2 Задание 3 Задание 1 Задание 2 Задание 3 Задание 1 Задание 2 Задание 3 Задание 1 Задание 2 Задание 3

Вариант 1 Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MNK. ответ

Вариант 1 ответ Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MNK. B N Х

Вариант 1 Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; С Є MND. А B С ответ

Вариант 1 ответ Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; С Є MND. А B С

Вариант 1 Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B М С ответ

Вариант 1 ответ Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B М С

Вариант 2 Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MDK. А B ответ

Вариант 2 ответ Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MDK. А B Х

Вариант 2 Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; В Є NDK. А B C ответ

Вариант 2 ответ Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; В Є NDK. А B C

Вариант 2 Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B С ответ

Вариант 2 ответ Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B N С

Вариант 3 Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MND. А B ответ

Вариант 3 ответ Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MND. А B N Х

Вариант 3 Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; В Є NDK. C B А ответ

Вариант 3 ответ Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; В Є NDK. C B А

Вариант 3 Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B С ответ

Вариант 3 ответ Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А B К С

Вариант 4 Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MDK. А B ответ

Вариант 4 ответ Задача № 1 Постройте точку пересечения прямой АВ с плоскостью MDK. А B Х

Вариант 4 Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; С Є MDN. А B C ответ

Вариант 4 ответ Задача № 2 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В и С; С Є MDN. А B C

Вариант 4 Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А С В ответ

Вариант 4 ответ Задача № 3 Постройте сечение тетраэдра плоскостью, проходящей через точки А, В, С. А С N В

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 966 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 339 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 689 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Усенко Ольга АлександровнаНаписать 5161 04.02.2016

Номер материала: ДВ-415338

04.02.2016 277

04.02.2016 1054

04.02.2016 352

04.02.2016 837

04.02.2016 2924

04.02.2016 1053

04.02.2016 590

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Названы главные риски для детей на зимних каникулах

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:ПОСТРОЕНИЕ СЕЧЕНИЙ ТЕТРАЭДРА ПЛОСКОСТЬЮСкачать

10 класс. Геометрия. Параллельные плоскости.

10 класс. Геометрия. Параллельные плоскости.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

1. Тетраэдр и его элементы

Как построить тетраэдр? Возьмем произвольный треугольник АВС. Произвольную точку D, не лежащую в плоскости этого треугольника. Получим 4 треугольника. Поверхность, образованная этими 4 треугольниками, и называется тетраэдром (Рис. 1.). Внутренние точки, ограниченные этой поверхностью, также входят в состав тетраэдра.

Рис. 1. Тетраэдр АВСD

Замечание: можно принять плоскость АВС за основание тетраэдра, и тогда точка D является вершиной тетраэдра. Каждое ребро тетраэдра является пересечением двух плоскостей. Например, ребро АВ – это пересечение плоскостей АВD и АВС. Каждая вершина тетраэдра – это пересечение трех плоскостей. Вершина А лежит в плоскостях АВС, АВD, АDС. Точка А – это пересечение трех означенных плоскостей. Этот факт записывается следующим образом: А = АВС ∩ АВD ∩ АСD.

Тетраэдр определение

Итак, тетраэдр — это поверхность, образованная четырмя треугольниками.

Ребро тетраэдра — линия перечесения двух плоскостей тетраэдра.

Видео:Как строить сеченияСкачать

2. Задача 1 на построение тетраэдра

Составьте из 6 спичек 4 равных треугольника. На плоскости решить задачу не получается. А в пространстве это сделать легко. Возьмем тетраэдр. 6 спичек – это его ребра, четыре грани тетраэдра и будут четырьмя равными треугольниками. Задача решена.

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

3. Задача 2 Построить сечение тетраэдра плоскостью

Дан тетраэдр АВСD. Точка M принадлежит ребру тетраэдра АВ, точка N принадлежит ребру тетраэдра ВD и точка Р принадлежит ребру DС (Рис. 2.). Постройте сечение тетраэдра плоскостью MNP.

Рис. 2. Рисунок к задаче 2 — Построить сечение тетраэдра плоскостью

Решение:
Рассмотрим грань тетраэдра DВС. В этой грани точки N и P принадлежат грани DВС, а значит, и тетраэдру. Но по условию точки N, P принадлежат секущей плоскости. Значит, NP – это линия пересечения двух плоскостей: плоскости грани DВС и секущей плоскости. Предположим, что прямые NP и ВС не параллельны. Они лежат в одной плоскости DВС. Найдем точку пересечения прямых NP и ВС. Обозначим ее Е (Рис. 3.).

Рис. 3. Рисунок к задаче 2. Нахождение точки Е

Точка Е принадлежит плоскости сечения MNP, так как она лежит на прямой NР, а прямая NР целиком лежит в плоскости сечения MNP.

Также точка Е лежит в плоскости АВС, потому что она лежит на прямой ВС из плоскости АВС.

Получаем, что ЕМ – линия пересечения плоскостей АВС и MNP, так как точки Е и М лежат одновременно в двух плоскостях — АВС и MNP. Соединим точки М и Е, и продолжим прямую ЕМ до пересечения с прямой АС. Точку пересечения прямых ЕМ и АС обозначим Q.

Итак, в этом случае NPQМ — искомое сечение.

Рис. 4. Рисунок к задаче 2.Решение задачи 2

Рассмотрим теперь случай, когда NP параллельна BC. Если прямая NP параллельна какой-нибудь прямой, например, прямой ВС из плоскости АВС, то прямая NP параллельна всей плоскости АВС.

Искомая плоскость сечения проходит через прямую NP, параллельную плоскости АВС, и пересекает плоскость по прямой МQ. Значит, линия пересечения МQ параллельна прямой NP. Получаем, NPQМ — искомое сечение.

Видео:ЕГЭ профиль: сечения часть 1Скачать

4. Задача 3 Построить сечение тетраэдра плоскостью

Точка М лежит на боковой грани АDВ тетраэдра АВСD. Постройте сечение тетраэдра плоскостью, которое проходит через точку М параллельно основанию АВС.

Рис. 5. Рисунок к задаче 3 Построить сечение тетраэдра плоскостью

Решение:
Секущая плоскость φ параллельна плоскости АВС по условию, значит, эта плоскость φ параллельна прямым АВ, АС, ВС.
В плоскости АВD через точку М проведем прямую PQ параллельно АВ (рис. 5). Прямая PQ лежит в плоскости АВD. Аналогично в плоскости АСD через точку Р проведем прямую РR параллельно АС. Получили точку R. Две пересекающиеся прямые PQ и РR плоскости РQR соответственно параллельны двум пересекающимся прямым АВ и АС плоскости АВС, значит, плоскости АВС и РQR параллельны. РQR – искомое сечение. Задача решена.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

5. Задача 4

Дан тетраэдр АВСD. Точка М – точка внутренняя, точка грани тетраэдра АВD. N – внутренняя точка отрезка DС (Рис. 6.). Построить точку пересечения прямой NM и плоскости АВС.

Рис. 6. Рисунок к задаче 4

Решение:
Для решения построим вспомогательную плоскость DМN. Пусть прямая DМ пересекает прямую АВ в точке К (Рис. 7.). Тогда, СКD – это сечение плоскости DМN и тетраэдра. В плоскости DМN лежит и прямая NM, и полученная прямая СК. Значит, если NM не параллельна СК, то они пересекутся в некоторой точке Р. Точка Р и будет искомая точка пересечения прямой NM и плоскости АВС.

Рис. 7. Рисунок к задаче 4. Решение задачи 4

Видео:Сечение тетраэдра? Легко! (в помощь студенту)Скачать

6. Задача 5 Построить сечение тетраэдра плоскостью

Дан тетраэдр АВСD. М – внутренняя точка грани АВD. Р – внутренняя точка грани АВС. N – внутренняя точка ребра DС (Рис. 8.). Построить сечение тетраэдра плоскостью, проходящей через точки М, N и Р.

Рис. 8. Рисунок к задаче 5 Построить сечение тетраэдра плоскостью

Решение:
Рассмотрим первый случай, когда прямая MN не параллельна плоскости АВС. В прошлой задаче мы нашли точку пересечения прямой MN и плоскости АВС. Это точка К, она получена с помощью вспомогательной плоскости DМN, т.е. мы проводим DМ и получаем точку F. Проводим СF и на пересечении MN получаем точку К.

Рис. 9. Рисунок к задаче 5. Нахождение точки К

Проведем прямую КР. Прямая КР лежит и в плоскости сечения, и в плоскости АВС. Получаем точки Р1 и Р2. Соединяем Р1 и М и на продолжении получаем точку М1. Соединяем точку Р2 и N. В результате получаем искомое сечение Р1Р2NМ1. Задача в первом случае решена.
Рассмотрим второй случай, когда прямая MN параллельна плоскости АВС. Плоскость МNР проходит через прямую МN параллельную плоскости АВС и пересекает плоскость АВС по некоторой прямой Р1Р2, тогда прямаяР1Р2 параллельна данной прямой MN (Рис. 10.).

Рис. 10. Рисунок к задаче 5. Искомое сечение

Теперь проведем прямую Р1М и получим точку М1. Р1Р2NМ1 – искомое сечение.

Видео:Построение сечения пирамиды по трем точкамСкачать

7. Итоги урока по теме «Тетраэдр», «Ребро тетраэдра», «Грани тетраэдра», «Поверхность тетраэдра», «Вершины тетраэдра»

Итак, мы рассмотрели тетраэдр, решили некоторые типовые задачи на тетраэдр. На следующем уроке мы рассмотрим параллелепипед.

📺 Видео

Сечение, параллельное заданной прямойСкачать

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

14. Задачи на построение сеченийСкачать

Построение сечений Занятие 1Скачать

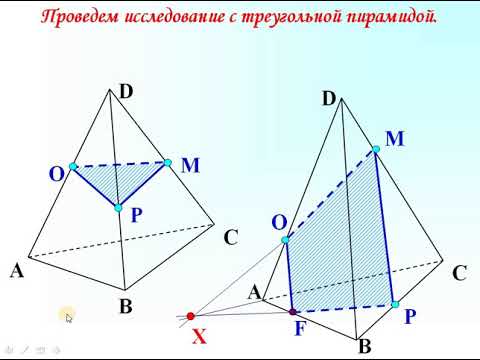
Построение сечения пирамиды. Метод следов.Скачать

СЕЧЕНИЯ ТЕТРАЭДРА И ПАРАЛЛЕЛЕПИПЕДАСкачать

Как строить сечения параллелепипедаСкачать

Построение сечений. Метод параллельных прямыхСкачать

ЕГЭ профиль: сечения часть 2Скачать

Как строить сечения в стереометрии? Задача 13Скачать