Почему по лобачевскому параллельные прямые пересекаются (6 видео)

Геометрия Лобачевского

Пятой аксиомой Евклида была аксиома о параллельных прямых, так называемый постулат о параллельных линиях, который гласит: если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. То есть эта аксиома утверждает, что существует только одна прямая, проходящая через данную точку вне данной прямой и параллельной этой данной прямой.

Сложная формулировка пятого постулата Евклида о параллельных линиях породила множество гипотез и предположений о возможной зависимости его от других постулатов. Были предприняты многочисленные попытки вывести его из остальных аксиом геометрии, но, к сожалению, они оказались тщетны. Усилия доказать пятый постулат от противного также не увенчались успехом.

И все же, в начале XX века почти одновременно несколько выдающихся математиков того времени — Карл Гаусс из Германии, Я. Больяи из Венгрии и Николай Иванович Лобачевский из России пришли к мысли о существовании другой, неевклидовой геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.

Поскольку Н. И. Лобачевский первым высказал эту идею в 1826 году, новая неевклидова геометрия была названа в его именем.

Геометрия Лобачевского имеет лишь одно отличие от евклидовой — аксиома параллельности заменяется на ее отрицание — аксиому параллельности Лобачевского.

Аксиома параллельности Лобачевского выглядит следующим образом:

Найдутся такая прямая a и такая не лежащая на ней точка A, что через A проходят по крайней мере две прямые, не пересекающие a.

Непротиворечивость аксиомы доказывается представлением модели, в которой реализуются данные аксиомы.

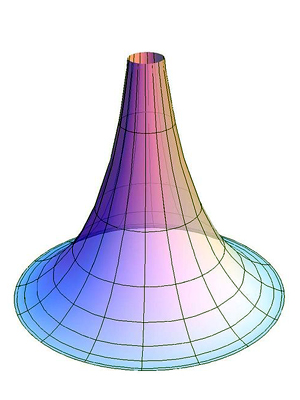
Основы аналитической геометрии, заложенные Лобачевским, практически наметили необходимую для доказательства модель. Лобачевский заметил, что орисфера в пространстве изометрична евклидовой плоскости. Полностью реализовать модель смогли работы Клейна, Пуанкаре и других ученых.

Геометрия Лобачевского нашла широчайшее применение в современной науке. Сам Николай Иванович Лобачевский использовал свою геометрию для вычисления определенных интегралов.

В теории функций комплексного переменного геометрия Лобачевского способствовала успешному построению теории автоморфных функций. В этой теории связь с геометрией Лобачевского была основой для исследований Пуанкаре. По словам Анри Пуанкаре, «неевклидова геометрия есть ключ к решению всей задачи».

Кроме того, геометрия Лобачевского стала использоваться в теории чисел, а именно, в ее геометрических методах, так называемой «геометрии чисел».

Ученые также установили тесную связь геометрии Лобачевского с кинематикой — специальной теорией относительности. В основе этой связи лежит равенство, выражающее закон распространения света:

x 2 + y 2 + z 2 = c 2 t 2 ,

при делении на t 2 , то есть для скорости света, даёт уравнение сферы в пространстве с координатами v_x, v_y, v_z, которые являются составляющими скорости света по осям х, у, z.

Преобразование Лоренца сохраняет эту сферу, а поскольку они линейны, переводят прямые пространства скоростей в прямые. Из этого следует, (согласно модели Клейна) что в пространстве скоростей внутри сферы радиуса с , значит есть для скоростей, меньших скорости света, имеет место геометрия Лобачевского.

В общей теории относительности геометрия Лобачевского также нашла свое место. Допуская возможным тот факт, что распределение масс материи во Вселенной равномерно (это приближение в космических масштабах допустимо), то при определенных условиях пространство имеет геометрию Лобачевского. Тем самым было доказано предположение Лобачевского о новой геометрии как возможной теории пространства.

Содержание

Новое в блогах
Пересекаются ли параллельные или Что говорил Лобачевский?
uCrazy.ru
Навигация
ЛУЧШЕЕ ЗА НЕДЕЛЮ
ОПРОС
СЕЙЧАС НА САЙТЕ
КАЛЕНДАРЬ
Сегодня день рождения
Рекомендуем
Мифы и заблуждения о геометрии Лобачевского
📹 Видео

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Новое в блогах

Видео:24. Параллельные линии могут пересекаться. Такое возможно?Скачать

Пересекаются ли параллельные или Что говорил Лобачевский?

Недавно в посте на околонаучные темы один из комментаторов завел разговор о геометрии Лобачевского (что он ее не понимает) и даже вроде попросил объяснить. Я тогда ограничилась утверждением, что понимаю. Объяснять эту теорию в ограниченных рамках комментария и одним текстом (без рисунков) показалось мне невозможным.

Однако, подумав, я все же решила попробовать дать небольшой популярный экскурс в эту теорию.

Немного предыстории. Геометрия со времен Евклида стала аксиоматической теорией, в которой большинство утверждений доказывалось на основе нескольких постулатов (аксиом). Считалось, что эти аксиомы «очевидны», т.е. отражают свойства реального (физического) пространства.

Одна из этих аксиом вызывала у ученых подозрение: а нельзя ли ее вывести из остальных постулатов? Современная формулировка этой аксиомы такова:

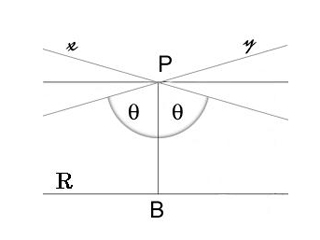
«Через точку, не лежащую на заданной прямой, можно провести не более одной прямой, параллельной ей». То, что одну-то прямую можно провести, является не аксиомой, а теоремой.

При этом «параллельной» называется прямая, не пересекающая данную. Итак, суть аксиомы в том, что такая прямая – одна!

(Распространенное утверждение «Лобачевский доказал, что параллельные прямые могут и пересекаться» — конечно, является вопиюще неправильным! Ведь это бы противоречило их определению!)

Лобачевский, как и многие до него, решил доказать, что это утверждение можно вывести из других аксиом. Для этого он, как это часто делается в математике, выбрал метод «от противного», т.е. предположил, что прямых, не пересекающих данную, больше одной и попытался вывести из этого противоречие с другими фактами. Но чем дальше он развивал теорию, тем больше убеждался, что никакого противоречия не предвидится! Т.е. получалось, что теория с «неправильным» постулатом тоже имеет право на существование!

Конечно, в первое время его выкладки не признавали, смеялись над ним. Именно поэтому великий Гаусс (который пришел к тем же выводам) не рискнул опубликовать свои результаты. Но со временем пришлось признать, что ЧИСТО ЛОГИЧЕСКИ теория Лобачевского ничем не хуже евклидовой.

Один из остроумных способов убедиться в этом – придумать такие «прямые», которые ведут себя как «прямые» Лобачевского. И математики нашли такой пример, и не один.

Пожалуй, самой простой является модель Пуанкаре. Вы можете сами построить ее нехитрыми приборами.

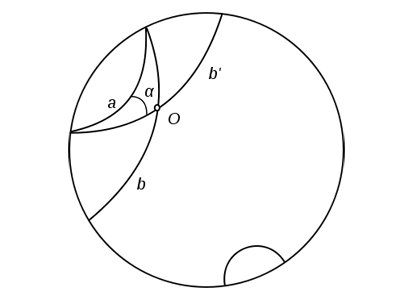
Начертите не листке бумаги прямую. Возьмите циркуль и, ставя его иглу на эту прямую, нарисуйте полуокружности, находящиеся с одной стороны от прямой. Теперь сотрите прямую (и с ней – концевые точки полуокружностей). Так вот, эти полуокружности «без концов» и будут вести себя, как прямые в геометрии Лобачевского!

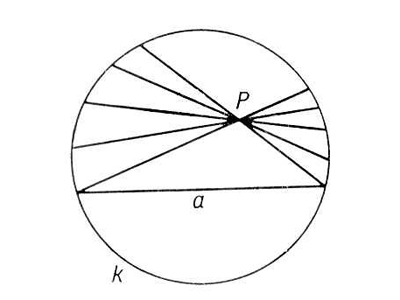
Действительно, выделим одну полуокружность и точку вне нее. Есть достаточно много полуокружностей, которые не пересекаются с исходной и все проходят через данную точку. Среди них выделяются две: они касаются нашей исходной «прямой» в концевых точках (которые мы, как Вы помните, стерли) Т.е. реального пересечения не происходит. Эти две окружности задают «границы», между которыми находятся все прямые, не пересекающие данную. Их – бесконечное количество.

Можно заметить, что треугольники в этой модели не такие, как на плоскости (евклидовой): сумма их углов меньше 180 градусов! Впрочем, чем меньше треугольник, тем больше сумма его углов. В «малом», на небольших расстояниях, геометрия Лобачевского практически совпадает с геометрией Евклида. Поэтому, вообще говоря, мы не сможем «экспериментально» отличить одну от другой, если окажется, что доступные нам (космические) расстояния– малы для этой цели.

Впрочем, в наше время ни физики, ни, тем более, математики, не пытаются воспринимать геометрию Лобачевского как модель «реального», физического пространства. Математики поняли, что все, что они могут сказать: если верны такие-то аксиомы, то верны и такие-то теоремы. Ну, а что такое «множества», «точки», «прямые», «углы», «расстояния», и т.п. – этого мы не знаем! Прямо как у Станислава Лема: «Сепульки – это объекты для сепулькирования»

«Говорят, Бертран Рассел определил математику как науку, в которой мы никогда не знаем, о чем говорим, и насколько правильно то, что мы говорим. Известно, что математика широко применяется во многих других областях науки. [ … ] Таким образом, одна из главных функций математического доказательства – создание надежной основы для проникновения в суть вещей.»

Видео:Что на самом деле доказал Лобачевский?Скачать

uCrazy.ru

ЛУЧШЕЕ ЗА НЕДЕЛЮ

ОПРОС

СЕЙЧАС НА САЙТЕ

КАЛЕНДАРЬ

Сегодня день рождения

Мифы и заблуждения о геометрии Лобачевского

Даже самые ленивые выпускники средней школы, у которых слово геометрия не вызывает ничего кроме скуки, что-то слышали о геометрии Лобачевского. Правда, кто такой Лобачевский, и чем его геометрия отличается от Евклидовой многие представляют весьма условно. Это и привело к появлению различных мифов связанных с именем Николая Ивановича Лобачевского и созданной им ветвью математики. Самых популярных мифов насчитывается 5 их и разберем ниже.

Миф 1. У геометрии Лобачевского нет ничего общего с Евклидовой

Когда Евклид создавал свою геометрию, он ввел множество различных понятий — что такое точка и линия, прямая и плоскость и некоторые другие. Среди введенных древнегреческим ученым понятий были и 5 постулатов (ныне мы их называем аксиомами), на основании которых он и выводил различные утверждения (теоремы).

Лобачевский для создания своей геометрии взял 4 первые постулата своего предшественника и коренным образам переработал пятый. Так что все теоремы, для доказательства которых не требуется обращаться к 5 постулату в обеих геометриях совпадают. Так что общего в построениях 2 великих ученых оказалось немало.

Миф 2. В геометрии Лобачевского параллельные прямые пересекаются

Незнакомые с геометрией Лобачевского люди утверждают, что в его научном построении параллельные прямые пересекаются. В качестве доказательства эти «знатоки» часто приводят в качестве примера железнодорожные рельсы, которые визуально пересекаются где-то в районе горизонта.

Но пересечение параллельных прямых относится к геометрии Римана, а у Лобачевского можно провести через точку, не лежащую на прямой, не менее 2, не пересекающих данную линию. На самом деле, прямых, не пересекающих данную через любую не лежащую на ней точку, можно провести бесконечное множество.

Представим в виде модели плоскости какой-нибудь эллипс. Его границу будем считать прямой бесконечно удаленных точек. Тогда 2 прямые проведенные через данную точку будут пересекаться непосредственно на границе эллипса. Они в геометрии Лобачевского и называются параллельными прямыми. Те же прямые, которые пересекаются с данной за границей эллипса именуются сверхпараллельными. Как видим, никакого пересечения параллельных прямых на плоскости нет.

Миф 3. Иных неевклидовых геометрий нет

Многие полагают, что только Лобачевскому удалось создать геометрию, отличную от Евклидовой. На самом деле есть еще геометрия Римана. Пятый постулат в трактовке Евклида гласит, что есть единственная прямая проходящая через конкретную точку и не пересекающая данную прямую. Согласно геометрии Лобачевского, таких прямых минимум 2 (на самом деле бесконечно много, вспомним сверхпараллельные).

Риман пошел еще дальше и предположил, что таких прямых нет в принципе — в его геометрии все прямые пересекаются. Проще всего представить глобус. Параллельные на экваторе друг другу меридианы сойдутся в одну точку на любом из полюсов.

Миф 4. Геометрия Лобачевского не применима в окружающем мире

Когда Лобачевский разрабатывал свою теорию, он полагал ее воображаемой. В самом деле, применить положения российского ученого в реальной жизни возможным не представлялось. Ситуация изменилась с созданием Альбертом Эйнштейном Общей Теории Относительности.

Согласно ее положениям, луч света двигающийся возле крупных тяготеющих масс должен искривляться, так как меняет свою кривизну само пространство. Дальнейшие наблюдения показали — вблизи Солнца лучи других звезд двигаются по законам геометрии Лобачевского.

Миф 5. Лобачевский является первооткрывателем неевклидовой геометрии

На самом деле «король математиков», немецкий ученый Карл Фридрих Гаусс, работал над теми же положениями, что и Лобачевский и пришел к созданию аналогичной геометрии, но опубликовать свои результаты не решился. Зато решился опубликовать свои результаты венгерский специалист Янош Больяи. Только он это сделал в написанном им предисловии к математической книге другого ученого. Научный мир теорию Больяи просто не заметил, а Лобачевский, видимо, и не слышал о венгерском ученом.