Построить горизонтальную проекцию треугольника abc плоскость которого параллельна прямой a

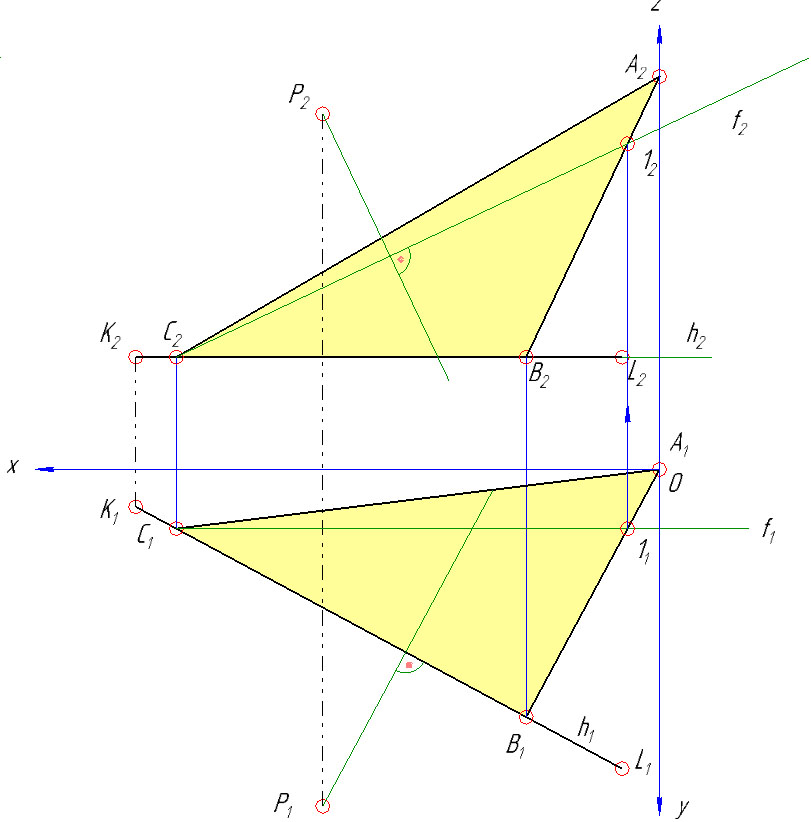
ЗАДАЧА№1

Построить проекции равнобедренного прямоугольного треугольника АВС, если известно, что катет ВС принадлежит прямой KL.

Исходными данными задачи является точка А – вершина треугольника и прямая KL, на которой расположен его катет ВС. Прямая KL – линия уровня (параллельна плоскости проекций П₁ или П₂).

РЕШЕНИЕ:

1) По заданным координатам в таблице с вариантами строим проекции точек А, Р и прямой KL, в нашей задаче KL параллельна П₁ – т.е. горизонталь (координаты по оси z равны 30).

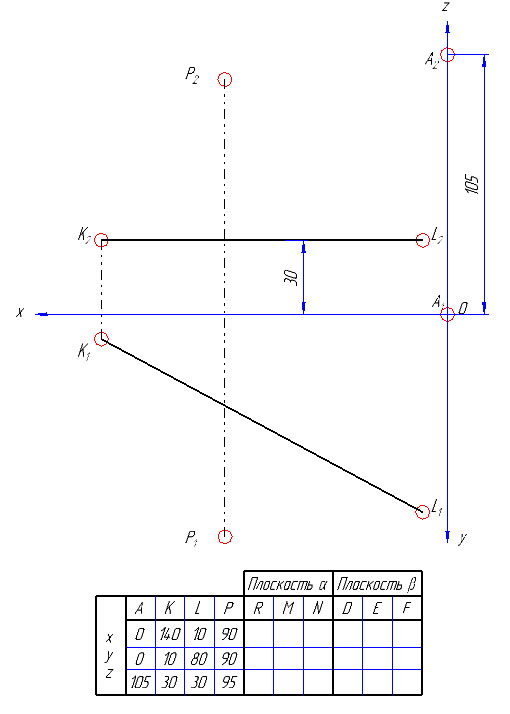
2) Из точки А опускаем перпендикуляр на прямую KL (так как искомый треугольник прямоугольный, а вершина А задана).

Отмечаем основание перпендикуляра – точку В (В₁). Фронтальную проекцию точки В (В₂) получаем по линии связи на К₂L₂.

3) Определяем натуральную величину катета АВ треугольника АВС способом прямоугольного треугольника: для этого на фронтальной проекции берем отрезок равный разнице координат проекций точек А и В – дельта z, и под прямым углом к горизонтальной проекции отрезка AB (A₁B₁) откладываем отрезок равный дельта z, получаем точку А₀. В₁А₀ – будет натуральной величиной катета (отрезка) АВ.

4) На прямой KL от точки В в любую сторону откладываем натуральную величину катета АВ (так как в равнобедренном прямоугольном треугольнике оба катета равны). В нашем случае откладываем на горизонтальной проекции K₁L₁ – т.к. KL – горизонталь и проецируется в натуральную величину именно на плоскость П₁. Получаем точку С (сначала проекцию С₁ и по линии связи C₂).

Соединяем точку А с точкой С. Треугольник АВС – искомый.

ЗАДАЧА№3

Определить натуральную величину расстояния от точки Р до плоскости.

РЕШЕНИЕ:

Кратчайшим расстоянием от точки до плоскости является отрезок перпендикуляра.

1) На основании теоремы о перпендикуляре к плоскости горизонтальная проекция перпендикуляра из точки Р проводится перпендикулярно к горизонтальной проекции горизонтали h. Независимо от горизонтальной проекции строится его фронтальная проекция. Для этого по плоскости найденного треугольника АВС проведена фронталь ƒ. Фронтальная проекция перпендикуляра должна быть перпендикулярна фронтальной проекции фронтали ƒ.

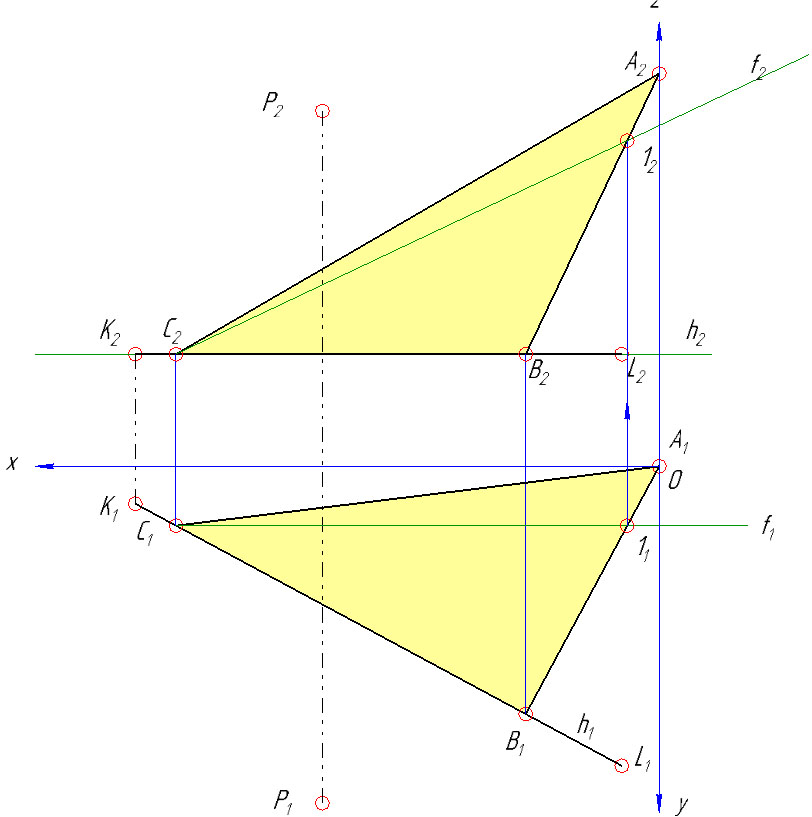
2) Прямая перпендикуляра из точки Р заключена в горизонтальнопроецирующую плоскость γ₁. Затем определена линия пересечения 2-3 вспомогательной плоскости γ с заданной плоскостью треугольника АВС.

В пересечении линии 2-3 с прямой n найдена искомая точка Q. Сначала определяется фронтальная проекция Q₂, а затем по линии проекционной связи определена ее горизонтальная Q₁ проекция.

3) Натуральная величина перпендикуляра PQ определена способом прямоугольного треугольника, аналогично как в задаче №1 определяли натуральную величину катета АВ.

Эпюра с задачами 1 и 3 — вариант 24

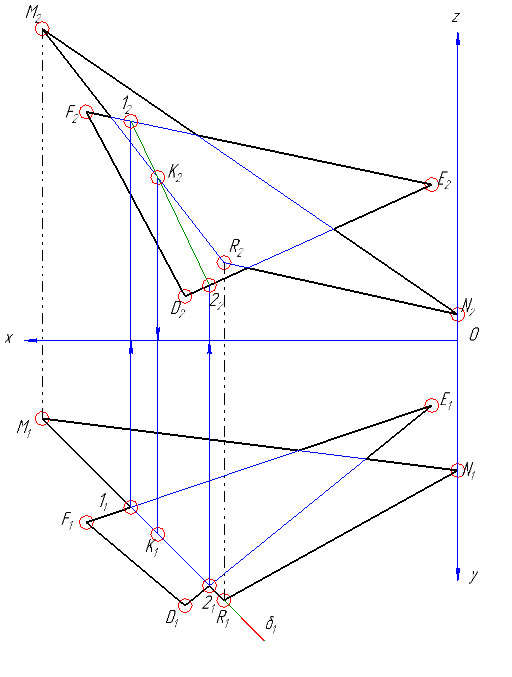
ЗАДАЧА №2.

Построить линию пересечения двух плоскостей заданных треугольниками α(DEF) и β(RMN), координаты вершин которых заданы в таблице исходных данных.

РЕШЕНИЕ:

1) По заданным координатам строим проекции всех точек, получаем проекции треугольников DEF и RMN.

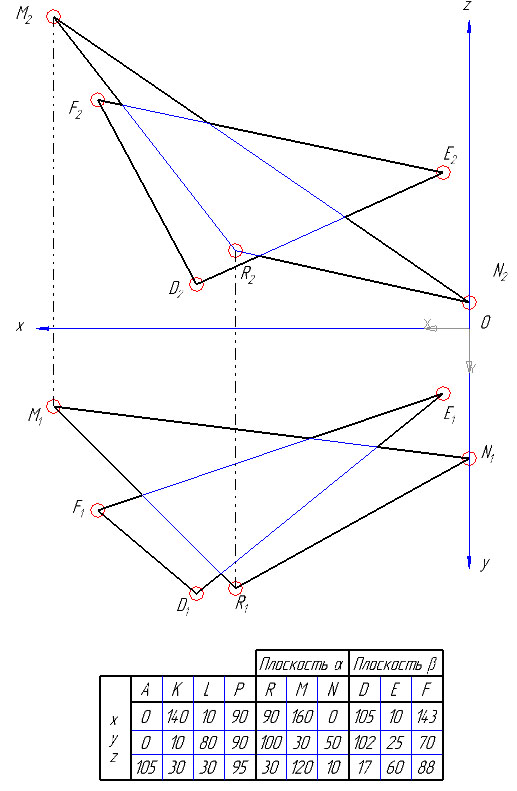
2) Решение задачи можно упростить, если вспомогательные проецирующие плоскости провести через прямые, задающие плоскость.

Так точка K этой линии определена с помощью горизонтальнопроецирущей плоскости δ₁, проведенной через сторону RM треугольника MNR. Именно линия RM является линией пересечения плоскости треугольника β(RMN) с вспомогательной плоскостью δ. Та же плоскость пересекает треугольник α(DEF) по линии 1-2.

Точка K, общая для трех плоскостей (двух заданных α и β и вспомогательной δ), находится в пересечении прямых 1-2 и RM.

Следует отметить, что если вспомогательная плоскость δ горизонтальнопроецирущая, то сначала определяется фронтальная проекция точки K₂, т.е. K₂ = 1₂-2₂∩R₂M₂, а затем по линии проекционной связи находится K₁ – горизонтальная проекция точки K.

3) Аналогично, заключая сторону DE во фронтальнопроецирующую плоскость γ₂, находится точка L. Прямая KL – линия пересечения заданных плоскостей.

4) Для определения видимости этих треугольников достаточно установить относительное расположение одной из сторон одного треугольника относительно стороны другого треугольника. Таким образом, вопрос видимости плоскостей сводится к определению видимости двух скрещивающихся прямых.

Определим видимость стороны DE треугольника DEF относительно стороны MN треугольника RMN на фронтальной плоскости проекции. Для этого проведем луч зрения s перпендикулярно П₂ через точку пересечения фронтальных проекций D₂E₂ и M₂N₂. В пересечении D₂E₂ и M₂N₂ расположены две конкурирующие по видимости точки (5₂ и 4₂). Точка 4 принадлежит стороне MN, а точка 5 – стороне DE. По горизонтальной проекции устанавливаем, что луч зрения сначала встретит D₁E₁ в точке 5₁, а затем M₁N₁ в точке 4₁. Следовательно, фронтальная проекция D₂E₂ – видима.

Аналогично определяется видимость треугольников и на горизонтальной проекции. Луч зрения при этом следует провести перпендикулярно к П₁ через две конкурирующие на П₁ точки скрещивающихся прямых (например, луч s / , проходящий через точки 1 и 6, соответственно принадлежащие прямым MR и ЕF).

Эпюр с задачей №2

ЗАКАЗЫВАЙТЕ ЧЕРТЕЖИ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ МГУПС

тел. (whatsup) 8-950-790-65-90

Видео:Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

РГР по начертательной геометрии

Ответы на вопросы по заказу заданий по начертательной геометрии:

Сколько стоит помощь?

• Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

Какой срок выполнения?

• Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

Если требуется доработка, это бесплатно?

• Доработка бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?

• Оценка стоимости бесплатна.

Каким способом можно оплатить?

• Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

Какие у вас гарантии?

• Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

В какое время я вам могу написать и прислать задание на выполнение?

• Присылайте в любое время! Я стараюсь быть всегда онлайн.

Содержание:

Примеры решения экзаменационных РГР по начертательной геометрии

Построить точку пересечения прямой а с плоскостью α, определить видимость.

а) Заключаем прямую a в плоскость β; α∩β=1₂

б) Находим проекцию точки 1 на плоскости π1

в) Проводим прямую а₂ до пересечения с осью х, получаем т. 2₂

г) Находим проекцию т. 2 в плоскости π1

е) Определяем видимость.

Возможно, вас также заинтересует эта ссылка:

Определить истинную величину отрезка АВ.

а) Проводим горизонталь h₂ через т. А₂

б) Полученное расстояние от т. В₂ до р откладываем на перпендикуляре от т. В₁ в плоскости π1

в) А₁ В₀₁ – истинная величина

Возможно, вас также заинтересует эта ссылка:

Найти величину перпендикуляра, опущенного из точки М на плоскость АВС.

а) Проводим в π2 горизонталь h₂ II оси х, замечаем точку 1_2, находим ее проекцию 1₁ в π1, проводим h₁

б) Проводим в π1фронталь f₁ II оси х, замечаем точку 2_1, находим ее проекцию 2₂ в π2, проводим f₂

в) Опускаем перпендикуляр из т. M₂ на f₂

г) Опускаем перпендикуляр из т. M₁ на h₁

д) Заключаем перпендикуляр из т. М₂ в плоскость α₂

е) Плоскость α₂ ∩ (ABC) = 3₂ 4₂, находим их проекции в плоскости π1

ж) Перпендикуляр, опущенный из т. М пересекается с 3₁ 4₁ в т. К₁ , находим проекцию т. К в π2

з) Находим длину МК, для этого в π2 замечаем длину перпендикуляра

М₂ К₂ = L (измерения производить перпендикулярно оси х)

и) В π1 перпендикулярно М₁ К₁ из т. М₁ выводим перпендикуляр и откладываем длину L, получаем т. М₀₁; длина К₁ М₀₁ – истинная величина перпендикуляра М К.

Возможно, вас также заинтересует эта ссылка:

Построить третью (профильную) проекцию пирамиды. Найти точку N на горизонтальной, профильной проекциях и в аксонометрической проекции пирамиды.

а)Строим профильную проекцию пирамиды:

— проецируем точки основания пирамиды и вершину на ось Z;

— с π1проецируем точки на ось Y, а затем под углом 45 0 на профильную плоскость π3;

— засекаем высоту вершины пирамиды относительно ее проекции в π2, получаем проекцию пирамиды на π3

б) Через существующую проекцию т. N и вершину пирамиды S проводим прямую до пересечения с ребром основания АВ, получаем т. 1₂ и находим ее проекции в плоскостях π1 и π3, соединяем с вершиной S

в) Перпендикулярно оси х проецируем т. Т на плоскость π1 и затем на π3

г) Строим аксонометрическую проекцию пирамиды, оси х, y выполняются под углом 120 0 относительно оси z, величины принимаются 1:1

д) Находим проекцию т. N в аксонометрии:

— соединяем т. 1 с проекцией вершины Sи находим проекцию т.N на данной прямой; поднимаем вертикальную ось из данной точки;

— далее соединяем т. 1 с вершиной S и на пересечении данной прямой 1S и вертикальной оси из горизонтальной проекции т. N будет определено месторасположеие т. N

Возможно, вас также заинтересует эта ссылка:

Определить расстояние между параллельными прямыми.

а) Производим замену плоскости π1 на π4 II прямым а₁ и b₁

б) Находим проекции прямых а₄ и b₄ согласно высотам в плоскости π2

в) Производим замену плоскости π4 на π5 перпендикулярно прямым а₄ и b_4; перпендикулярно оси х₄₅ переносятся проекции прямых, проецирующихся в точку (расстояния от оси х₄₅ откладываются согласно расстоянию от прямых до оси х₁₄)

г) Полученное расстояние между прямыми а₅ и b₅ , спроецированные в точку – L истинная величина

Возможно, вас также заинтересует эта ссылка:

Построить точку пересечения прямой L с плоскостью ABC, определить видимость

а) Заключаем прямую L в плоскость α₂

б) Она засекает т. 1 и 2 в π2, находим проекции точек в плоскости π1

г) Находим проекцию К₂ в π2

д) Определяем видимость

Возможно, вас также заинтересует эта ссылка:

Определить какой из отрезков длиннее

а) т.к. прямая АС II оси х₁₂ – она является фронталью и уже имеет натуральную величину,

б) Определяем натуральную величину АВ:

— проводим в π2 через т. А горизонталь h₂ II оси х;

— опускаем из т. B₂ перпендикуляр на горизонталь;

в) Откладываем в π1 на перпендикуляре от АВ из т. В длину перпендикуляра, получаем т. В₀₁; отрезок А₁ В₀₁ – истинная аеличина

г) Сравниваем длины отрезков Н.В. : АС >АВ

Возможно, вас также заинтересует эта ссылка:

Способом замены плоскостей проекций определить истинную величину треугольника АВС

а) Проводим из т. С₂ горизонталь h₂ II оси х, на АВ замечаем т. 1₂, проецируем ее в π1, находим т. 1₁ на А₁ В₁

б) Перпендикулярно h₁ в проекции С производим замену плоскости проекций π4

в) Проецируем точки АВС на π4 перпендикулярно оси х₁₄ и отмечаем проекции точек согласно высотам в плоскости π2 соответственных точек

г) II А₄ В₄ С₄ вводим плоскость π5 и проецируем перпендикулярно оси х₄₅; точки А₅ В₅ С₅, откладываем на расстоянии от точек А₁ В₁ С₁ до х₁₄

д) А₅ В₅ С₅ – натуральная величина плоскости АВС

Построить сечение пирамиды плоскостью, заданной двумя пересекающимися прямыми. Найти его натуральную величину

а) В плоскости π1 перпендикулярно h₁ производим замену плоскости проекций π4; сносим проекции точек пирамиды и плоскости (h∩f)

б) Плоскость (h∩f) занимает в π4 проецирующее положение, она пересекает SAВСD в точках 2₄ , 3₄ , 4 ₄, 5₄; находим их проекции в π1 и π2

в) Строим натуральную величину сечения 2345, для этого производим замену плоскости проекции π4 на π5 II (h₄ ∩f₄ ), и перпендикулярно оси х₄₅ проецируем точки сечения в новую плоскость

г) Для определения месторасположения точек рассмотрим π1, находим длины отрезков от точек сечения до оси х₁₄ и отмечаем соответствующие длины на соответствующих проекциях точек сечения

д) Соединяем полученные точки получаем сечение 2345 – натуральная величина

Определить точки пересечения прямой L с конусом

а) Прямую L₂ заключаем в плоскость α₂, α₂ пересекает поверхность конуса, проецируем точки пересечения на горизонтальную ось конуса в проекции π1, и проводим данным радиусом окружность

б) Проведенная окружность пересекает проекцию прямой L₁ в точках 1₁ 2₁, находим проекции точек в π2 – 1₂ 2₂

в) Определяем видимость.

Построить сечение конуса и цилиндра, определить видимость

а) Рассмотрим проекции тел вращения в π2:

— образующая конуса S₂ K₂ пересекает цилиндр в т. 1₂ и 2₂, проецируем точки на горизонтальную ось конуса, проходящую через вершину S, в плоскости π1;

б) В плоскости π2 проводим секущие плоскости α₁, α₂, α₃, α₄, данные плоскости пересекают и конус и цилиндр, находим общие точки пересечения, проецируем их в π1на соответствующие сечения плоскостями

в) Соединяем точки сечения

г) Определяем видимость

Построить точку пересечения прямой а с плоскостью α, определить видимость

а) Заключаем прямую a в плоскость β; α∩β=1₂

б) Находим проекцию точки 1 на плоскости π1

в) Проводим прямую а₂ до пересечения с осью х, получаем т. 2₂

г) Находим проекцию т. 2 в плоскости π1

е) Определяем видимость.

Достроить горизонтальную проекцию многоугольника АВСDE и найти его натуральную величину

а) Соединяем A₂ D ₂ ; из точки Е₂ проводим прямую через т. С₂; A₂ D ₂ ∩ Е₂ С₂=1₂; находим проекцию т. 1₁ и проводим через нее и т. Е₁ прямую; прямая Е₁1₁ пересекается с проекционной линией т. С, получаем ее горизонтальную проекцию С₁

б) Определяем месторасположение т. В₁:

— в проекции π2 через т.В₂ и 1₂ проводим прямую, пересекающую сторону Е₂ D ₂ в точке 2₂, находим ее проекцию в π1т. 2₁;

— в проекции π1проводим прямую 1₁ 2₁ до пересечения с проекционной линией т. В, получаем ее горизонтальную проекцию В₁;

г)Определяем натуральную величину А ЕDCB:

— в π2 через т. Е₂ проводим горизонталь h₂; h₂ ∩ В₂ С₂=3₂; находим ее горизонтальную проекцию на В₁ С₁, определяем положение h₁;

— перпендикулярно h₁ вводим новую проекцию π4 и проецируем на нее, перпендикулярно оси х₁₄, плоскость АЕDCB (она занимает проецирующее положение);

— II А₄ Е₄ D₄ C₄ B₄ вводим новую плоскость π5 и проецируем на нее точки плоскости, с учетом длин в проекции π1, т.е. удаление от точек проекции π1 до оси х₁₄

— соединяем получившиеся точки, А₅ Е₅D₅ C₅B₅ — натуральная величина

Найти величину перпендикуляра, опущенного из точки М на плоскость АВС

а) Проводим в π2 горизонталь h₂ II оси х, замечаем точку 1_2, находим ее проекцию 1₁ в π1, проводим h₁

б) Проводим в π1фронталь f₁ II оси х, замечаем точку 2_1, находим ее проекцию 2₂ в π2, проводим f₂

в) Опускаем перпендикуляр из т. M₂ на f₂

г) Опускаем перпендикуляр из т. M₁ на h₁

д) Заключаем перпендикуляр из т. М₂ в плоскость α₂

е) Плоскость α₂ ∩ (ABC) = 3₂ 4₂, находим их проекции в плоскости π1

ж) Перпендикуляр, опущенный из т. М пересекается с 3₁ 4₁ в т. К₁ , находим проекцию т. К в π2

з) Находим длину МК, для этого в π2 замечаем длину перпендикуляра

М₁ К₁ = L (измерения производить перпендикулярно оси х)

и) В π1 перпендикулярно М₁ К₁ из т. М₁ выводим перпендикуляр и откладываем длину L, получаем т. М₀₁; длина К₁ М₀₁ – истинная величина перпендикуляра М К.

Построить три проекции точек, заданных координатами: А (-30; 10;20), В (40;20;15), С (20; -40; 15)

• а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
• б) Каждая точка должна иметь три проекции.

16. Построить линию пересечения призмы и конуса.

а) Рассмотрим π1: находим середины сторон призмы: 1₁, 2₁, 3₁ и их проекции во фронтальной плоскости

б) Продливаем прямые S₁ 3₁; S₁ 2₁;S₁ 1₁ до пересечения с основанием конуса в т. 6 ₁,5₁,4₁ соответственно

г) Определяем точки пересечения данных прямых с проекциями середин отрезков призмы

д) Определяем линию пересечения призмы и конуса

Построить линию пересечения двух плоскостей, определить видимость линий

• а) Рассмотрим π1
• б) Через ребра D₁ F₁ и D₁ E₁ пропускаем плоскости α₁ и β₁, α∩ (ABC) = 1₁ 2₁; β∩ (ABC)=3 ₁4₁
• в) Находим проекции прямых в π2; 1₂ 2₂∩ D₂ F₂=К₂; 3 ₂4₂∩ D₂ E₂=М₂; находим проекции К ₂М ₂ в плоскости π1
• г) КМ – линия пересечения
• д) Определяем видимость с помощью конкурирующих точек

Построить точку пересечения прямой L с плоскостью ABC, определить видимость

а) Рассмотрим π2

б) Через вершину А₂ и проекцию прямой L₂ (точка) проводим прямую и засекаем ее в плоскость α₂; α₂∩( ABC)= 1₂; находим ее проекцию в π1и соединяем с вершиной А₁

в) 1₁ А₁ ∩ L₁=М₁— точка пересечения прямой и плоскости

Построить вторую проекцию прямой, принадлежащей плоскости α

а) Проецируем точки прямой на плоскость α π2 и определяем проекции на ось х₁₂

б) II α π1 из проекций на оси х₁₂ проводим лучи, засекающие проекционные лучи точек прямой АВ в точках А ₁В₁

Построить линию пересечения плоскости i со сферой

а) Плоскость i засекает сферу в π2 в т. 1₂ 2₂; проецируем точки на горизонтальную ось проекции π1, получаем т. 1₁ 2₁

б) Плоскость пересекает сферу в т. 3₂ , находим ее проекции 3₁ 3`₁;

Построить три проекции точек, заданных координатами: А (-40; -10;20), В (40;20;-60), С (20; 40; 15)

а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;

б) Каждая точка должна иметь три проекции.

Построить призму SABC в аксонометрической проекции

г) Строим аксонометрическую проекцию пирамиды, оси х, y выполняются под углом 120 0 относительно оси z, величины принимаются 1:1

Построить сечение способом концентрических сфер

а) Находим центр пересечения осей конусов 0₂

б) Опускаем из 0₂ перпендикуляр на образующую прямого конуса, получаем т. S₂, проводим луч II основанию прямого конуса.

в) Окружность радиусом R1 пересекает образующую наклонного конуса в т. 1₂; II основанию наклонного конуса проводим луч из т. 1_2, который пересекает луч из т. S₂ в точке 2₂

г)Рассмотрим видимые пересечения конусов в точках 3₂ и 4₂

д) Соединяем получившиеся точки 2₂, 3₂, 4₂ – линия пересечения двух конусов.

Построить точку пересечения прямой L с плоскостью ABC, определить видимость

а) Рассмотрим π1

б) Через вершину А₁ и проекцию прямой L₁ (точка) проводим прямую и засекаем ее в плоскость α₁; α₁∩( ABC)= 1₁; находим ее проекцию в π2и соединяем с вершиной А₂

в) 1₂ А₂ ∩ L₂=М₁— точка пересечения прямой и плоскости

Построить вторую проекцию треугольника АВС, принадлежащего плоскости α

а) Рассмотрим π2,проецируем точки плоскоасти АВС на проекцию απ2 II оси х₁₂ получаем точки А`<sub>2,</sub> В`_2, С`₂ и проецируем их на ось х₁₂

б) II плоскости απ1 из проекций А`<sub>1,</sub> В`_1, С`₁ проводим лучи, которые засекутся с проекциями точек А_2, В_2, С₂ в проекциях точек А_1, В_1, С₁

Построить линию пересечения плоскости i с конусом

а) Плоскость i сечет конус в точках 1₂2₂, проецируем их в π1 на горизонтальную ось конуса

б) i₂ пересекает вертикальную ось конуса в т. 3₂ перпендикулярно вертикальной оси конуса проводим секущую плоскость; получившимся радиусом R1 в π1проводим окружность и проецируем на данную окружность проекции точек 3₁ 3`₁

в) Определяем сечение и видимость.

Построить три проекции точек, заданных координатами: А (40; -10;20), В (30;20;-60), С (-20; -40; -15)

а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;

б) Каждая точка должна иметь три проекции.

Определить расстояние между параллельными прямыми а и b

• а) В плоскости π1 II прямым а₁ , b₁ вводим новую плоскость π4 и перпендикулярно ей проецируем точки, задающие прямые
• б) Откладываем от оси х₁₂ высоты, соответствующие высотам прямых а₂ , b₂ в плоскости π2, находим проекции прямых а₄ , b₄
• в)Задаем новую плоскость π5перпендикулярно проекциям прямых а₄ , b_4, проводим проекционные лучи перпендикулярно оси х₄₅
• г)Прямые в данной плоскости будут проецироваться в точку, рассмотрим π1; замечаем расстояния от прямых до оси х_14, и откладываем их на проекционных лучах в плоскости π5.
• д) Расстояние между проекциями прямых а₅ , b₅ — искомое.

Определить точку пересечения L с плоскостью, заданной прямыми АВ и АС

а) Рассмотрим π2

б) Через вершину А₂ и проекцию прямой L₂ (точка) проводим прямую и засекаем ее в плоскость α₂; α₂∩( ABC)= 1₂; находим ее проекцию в π1и соединяем с вершиной А₁

в) 1₁ А₁ ∩ L₁=М₁— точка пересечения прямой и плоскости

Построить вторую проекцию плоского четырехугольника, если даны три точки, принадлежащие его плоскости

а) Соединяем точки АВС; в π2 проводим диагонали у четырехугольника К₂ М₂ Р ₂Т₂

б) Диагонали пересекают плоскость АВС в точках 6₂ 5₂ 4₂ 3₂

в) Сторона четырехугольника МР∩( ABC)= 1₂ и 2₂

г) Находим проекции 1₁ 2₁ 3₁ 4₁ 5₁ 6₁ в плоскости π1 на соответствующих сторонах плоскости

д)Определяем диагонали и находим на них с помощью проекционных лучей из плоскости π2 проекции точек К₁ М₁ Р ₁Т₁

Вращением вокруг оси i совместить точку К с плоскостью α

а) II оси х₁₂ в проецируем проекцию т. К на проекцию плоскости απ2 , получаем т. 1₂ находим ее горизонтальную проекцию 1₁

б) В π1 II плоскости απ1из т. 1₁ проводим луч

в) i – ось вращения, вращаем т. К₁,до совмещения ее с лучом из т. 1₁, получаем т. К’₁

г) Находим на пересечении проекционных лучей т К.

Построить три проекции точек, заданных координатами: А (-35; -10;-20), В (30;20;60), С (-20; -40; 15)

а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;

б) Каждая точка должна иметь три проекции.

Построить точки пересечения прямой I со сферой

а) Через прямую i в π2 проводим α₂

в) Находим проекции точек в π1и проводим окружность R=1₁0₂

г) Окружность пересекает прямую I в точках 3 ₁4₁

д) Определяем видимость

Возможно, вас также заинтересует эта ссылка:

Построить линию пересечения двух плоскостей, определить видимость линий

а) Рассмотрим π1

г) КМ – линия пересечения

д) Определяем видимость с помощью конкурирующих точек

Построить линию пересечения прямой с и плоскости, заданной параллельными прямыми a и b

Построить три проекции точек, заданных координатами: А (35; -10;-20), В (30;20;60), С (-20; -40; 15)

а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;

б) Каждая точка должна иметь три проекции.

Разделить отрезок АВ точкой С в отношении АС:АВ=3:2

а) Через т. А₂ проводим горизонталь h₂ в плоскости π2, замечаем расстояние от т. В₂ до горизонтали и в проекции π1 откладываем его на перпендикуляре отрезку А ₁В₁, получаем т. В’₁, А₁ В’₁ – натуральная величина АВ.

б) На А₁ В’₁ откладываем равные между собой отрезки количеством 3+2=5; Соединяем В’₁ с В₁ и II В’₁ В₁ находим проекции равных по величине отрезков

в)Определяем положение. С₁ на отрезке А ₁В₁ а заданной пропорции АВ:СВ=3:2

г) Находим проекцию т. С₂ в π2

Построить точки пересечения полусферы с прямой а, показать видимость

а) Через прямую а₂ в π2 проводим α₂

б) α₂∩ с полусферой по ее образующей

в) Находим проекции точек в π1 на горизонтальной оси полусферы и проводим окружность данным радиусом

г) Окружность пересекает прямую I в точках 1₁2₁, находим их проекции в π2

д) Определяем видимость

Определить расстояние от т. А до плоскости MNK

а) Проводим в π2 горизонталь h₂ II оси х, замечаем точку 1_2, находим ее проекцию 1₁ в π1, проводим h₁

б) Проводим в π1фронталь f₁ II оси х, замечаем точку 2_1, находим ее проекцию 2₂ в π2, проводим f₂

в) Опускаем перпендикуляр из т. А₂ на f₂

г) Опускаем перпендикуляр из т. А₁ на h₁

д) Заключаем перпендикуляр из т. А₂ в плоскость α₂

е) Плоскость α₂ ∩ (MKN) = 3₂ 4₂, находим их проекции в плоскости π1

ж) Перпендикуляр, опущенный из т. А пересекается с 3₁ 4₁ в т. В₁ , находим проекцию т. В в π2

з) Находим длину АВ, для этого в π1 замечаем длину перпендикуляра

А₂ В₂ = L (измерения производить перпендикулярно оси х)

и) В π2 перпендикулярно А₂ В₂ из т. А₂ выводим перпендикуляр и откладываем длину L, получаем т. А₀₂; длина В₁ А₀₁ – истинная величина перпендикуляра АВ.

Построить сечение пирамиды плоскостью, заданной фронталью и горизонталью

а) В плоскости π1 перпендикулярно h₁ производим замену плоскости проекций π4; сносим проекции точек пирамиды и плоскости (h∩f)

б) Плоскость (h∩f) занимает в π4 проецирующее положение, она пересекает SAВС в точках 2₄ , 3₄ , 4 ₄, 5₄; находим их проекции в π1 и π2

в) Соединяем полученные точки получаем сечение 2₂ 3₂ 4₂ 5 ₂

Построить точку пересечения прямой С с плоскостью, заданной пересекающимися прямыми а и b

а) В плоскости π1через прямую проводим плоскость α₁, она засекает плоскость (a ∩ b) (ABS) в точках 1₁2₁, находим их проекции в π2

б) 1₂2₂∩ с₂ =Р₂ – точка пересечения прямой с и (a ∩ b)

Построить три проекции точек, заданных координатами: А (35; -10;-20), В (30;20;60), С (-20; -40; -15)

а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;

б) Каждая точка должна иметь три проекции.

Способом замены плоскостей проекций определить истинную величину треугольника АВС

а) Проводим из т. С₂ горизонталь h₂ II оси х, на АВ замечаем т. 1₂, проецируем ее в π1, находим т. 1₁ на А₁ В₁

б) Перпендикулярно h₁ в проекции С производим замену плоскости проекций π4

в) Проецируем точки АВС на π4 перпендикулярно оси х₁₄ и отмечаем проекции точек согласно высотам в плоскости π2 соответственных точек

г) II А₄ В₄ С₄ вводим плоскость π5 и проецируем перпендикулярно оси х₄₅; точки А₅ В₅ С₅, откладываем на расстоянии от точек А₁ В₁ С₁ до х₁₄

д) А₅ В₅ С₅ – натуральная величина плоскости АВС

Построить проекции точки А, которая принадлежит плоскости β общего положения, заданной параллельными прямыми а и b

а)т.к. т. А принадлежит плоскости, заданной (a II b), то через т. А мы можем провести горизонталь h₂ в π2; h₂∩(a₂ II b₂)= 1₂2₂, находим их проекции в π1

б) из т. А2 опускаем проекционный луч в π1; пересечение луча и 1₁2₁ –искомая проекция т. А.

Построить линию пересечения плоскости, заданной пересекающимися прямыми a и b и прямыми с и d

а) Конусы в основании пересекаются в точках 1₂2₂, находим их проекции в π1

б) В π1проводим секущие плоскости II оси х₁₂; данные плоскости пересекают два конуса; отмечаем радиусы пересечения и проецируем их на плоскость π2 на горизонтальную ось конусов; проводим окружности; пересечение окружностей, образованных сечением одной плоскости, дают точки пересечения двух конусов.

в) Соединяем получившиеся точки в π2 и проецируем их на соответствующие секущие плоскости в π1, соединяем линию пересечения

г) Определяем видимость

Построить линию взаимного пересечения поверхностей, определить видимость

а) Через две плоскости пропускаем секущие плоскости γ₁; γ₂

д) Находим проекции точек в π2

е) N D- линия пересечения плоскостей

Построить точку пересечения прямой с и плоскости, заданной параллельными прямыми а и b

а) Рассмотрим π2

б) Через проекцию прямой с₂ (точка) проводим прямую и засекаем ее в плоскость α₂; α₂∩( a II b)= 1₂2₂; находим их проекции в π1-1₁2₁

в) 1₁ 2₁ ∩ с₁=S₁— точка пересечения прямой и плоскости

Построить фронтальную проекцию кривой m, принадлежащей плоскости α

а)Выделяем на кривой m₁ несколько ключевых точек: 2₁ 3₁ 4₁ 5 ₁

б) Рассмотрим π1,проецируем точки кривой m₁ на проекцию απ1 II оси х₁₂ получаем точки 2’₁ 3’₁ 4’₁ 5’ ₁и проецируем их на ось х₁₂ получаем точки 2’₂ 3’₂ 4’₂ 5’ ₂

б) II плоскости απ2 из проекций 2’₂ 3’₂ 4’₂ 5’ ₂ проводим лучи, которые засекутся с проекционными лучами, выпущенными из точек 2₁ 3₁ 4₁ 5₁, в проекциях точек 2₂ 3₂ 4₂ 5 ₂

Способом замены плоскостей проекций определить истинную величину фигуры

а) Проводим из т. А₂ горизонталь h₂ II оси х, на СВ замечаем т. 1₂, проецируем ее в π1, находим т. 1₁ на С₁ В₁

б) Перпендикулярно h₁ в проекции π1 производим замену плоскости проекций на π4

в) Проецируем точки АВС на π4 перпендикулярно оси х₁₄ и отмечаем проекции точек согласно высотам в плоскости π2 соответственных точек

г) II А₄ В₄ С₄ вводим плоскость π5 и проецируем перпендикулярно оси х₄₅; точки А₅ В₅ С₅, откладываем на расстоянии от точек А₁ В₁ С₁ до х₁₄

д) А₅ В₅ С₅ – натуральная величина плоскости АВС

Определить расстояние от точки D до плоскости, заданной ∆АВС

а) Проводим в π2 горизонталь h₂ II оси х, замечаем точку 1_2, находим ее проекцию 1₁ в π1, проводим h₁

б) Проводим в π1фронталь f₁ II оси х, замечаем точку 2_1, находим ее проекцию 2₂ в π2, проводим f₂

в) Опускаем перпендикуляр из т. D₂ на f₂

г) Опускаем перпендикуляр из т. D₁ на h₁

д) Заключаем перпендикуляр из т. D₂ в плоскость α₂

е) Плоскость α₂ ∩ (ABC) = 3₂ 4₂, находим их проекции в плоскости π1

ж) Перпендикуляр, опущенный из т. D пересекается с 3₁ 4₁ в т. M₁ , находим проекцию т. M в π2

з) Находим длину DM, для этого в π2 замечаем длину перпендикуляра

D₁ M₁ = L (измерения производить перпендикулярно оси х)

и) В π1 перпендикулярно D₁ M₁ из т. D₁ выводим перпендикуляр и откладываем длину L, получаем т. D₀₁; длина M₁ D₀₁ – истинная величина перпендикуляра D M.

Построить точки пересечения прямой со сферой

а) Через прямую i₂ в π2 проводим α₂

б) α₂∩ со сферой в точках 1₂ 2₂ по образующей сферы, и в т. 3₂ в центральной т. проекции сферы

в) Находим проекции точек в π1 на горизонтальной оси сферы 1₁2₁ и 3₁, 3’₁ в месте пересечения вертикальной оси и образующей сферы

г) Проводим сечение 1₁2₁ 3₁3’₁ , оно пересекает прямую i в точках К₁Р₁, находим их проекции в π2

д) Определяем видимость

Построить линию пересечения конуса и полусферы, определить видимость

а) Конус и сфера в π1 пересекаются в т. 1₁2₁; находим их проекции в π2

б) В π2 проводим секущие плоскости II оси х₁₂; данные плоскости пересекают конус и сферу; отмечаем радиусы пересечения и проецируем их на плоскость π1 на горизонтальную ось конуса и сферы; проводим окружности; пересечение окружностей, образованных сечением одной плоскости, дают точки пересечения сферы и конуса.

в) Соединяем получившиеся точки в π1 и проецируем их на соответствующие секущие плоскости в π2, соединяем линию пересечения

г) Определяем видимость

Построить точку пересечения прямой а с плоскостью α

а) Проводим через прямую а в π2 горизонталь h₂

б) из т. 1₁ II α π1 проводим луч, пересекающий прямую а в точке М ₁ – точка пересечения а с плоскостью α

Построить третью проекцию точек и записать их координаты

а) Определяем существующие координаты точек с учетом индексов точек, заданных координатами осей x,y,z.

б) М(28, 15,15); С(-10;0;10); А(-22;30;-10); В(15;0;19)

Определить расстояние между точками А и В

а) Соединяем точки А и В в отрезок

а) Проводим горизонталь h₂ через т. В₂

б) Полученное расстояние от т. А₂ до h₂ откладываем на перпендикуляре от т. А₁ в плоскости π1

Построить точки пересечения прямой L с конусом

• а) Прямую L₂ заключаем в плоскость α₂, α₂ пересекает поверхность конуса, проецируем точки пересечения 1₂ 2₂ на горизонтальную ось конуса в проекции π1-1₁ 2₁ , и проводим данным радиусом окружность
• б) Проведенная окружность пересекает проекцию прямой L₁ в точках А₁ В₁, находим проекции точек в π2 –А₂ В₂
• в) Определяем видимость

Построить прямоугольную изометрию правильной пятиугольной пирамиды SABCDE

а) Строим аксонометрическую проекцию многогранника, оси х, y выполняются под углом 120 0 относительно оси z, величины принимаются 1:1

Построить точку пересечения прямой L с плоскостью ABC, определить видимость

а) Заключаем прямую L в плоскость α₂

б) Она засекает т. 1 и 2 в π2, находим проекции точек в плоскости π1

г) Находим проекцию К₂ в π2

д) Определяем видимость

Построить три проекции прямой А (0; 25;50), В (20;30;30), найти его натуральную величину

а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;

б) Находим третью проекцию прямой:

— откладываем значение y по горизонтали с правой стороны от оси z и находим проекции точек согласно фронтальным проекциям точек

в) Находим Н.В.- проводим в π2 из т. В₂ горизонталь h₂;

— полученное расстояние от т. А₂ до h₂ откладываем на перпендикуляре от т. А₁ в π1;

Построить горизонтальную проекцию точки А, которая принадлежит плоскости, заданной прямой BC и точкой В

а) Определяем плоскость ВСD

б) Через т. А₂ II оси х₁₂ проводим горизонталь h₂

в) h₂ ∩ ВСD=1₂ 2₂,находим их проекции на соответствующих сторонах плоскости ABCDи проводим горизонталь h₁

г) т.к. горизонталь пропущена через т. А₂, то проекция А₁ будет лежать на горизонтали h₁ и проекционном луче из т. А₂.

Достроить горизонтальную проекцию четырехугольника ABCD

а) Для определения местоположения т. О следует в π2 провести диагонали четырехугольника АВСD

в) Через В₁ и проводим прямую, засекающую т. D₁ на проекционном луче из т. D₂

Определить линию пересечения плоскостей, заданных пересекающимися прямыми с и d и а и b

а) Через две плоскости пропускаем секущие плоскости γ₁; γ₂

д) Находим проекции точек в π2

е) N D- линия пересечения плоскостей

Построить линию пересечения цилиндра и шара

а) Цилиндр и сфера в π1 пересекаются в т. 1₁2₁; находим их проекции 1₂2₂

в π2 на горизонтальной оси сферы

б) В π2 проводим секущие плоскости II оси х₁₂; данные плоскости пересекают цилиндр и сферу; отмечаем радиусы пересечения и проецируем их на плоскость π1 на горизонтальную ось цилиндра и сферы; проводим окружности; пересечение окружностей, образованных сечением одной плоскости, дают точки пересечения сферы и конуса.

в) Соединяем получившиеся точки в π1 и проецируем их на соответствующие секущие плоскости в π2, соединяем линию пересечения

г) Определяем видимость

Построить точку пересечения прямой L с плоскостью ABC, определить видимость

а) Заключаем прямую L в плоскость α₁

б) Она засекает т. 1 и 2 в π1, находим проекции точек в плоскости π2

г) Находим проекцию К₁ в π1

д) Определяем видимость

Построить три проекции прямой А (50; 15;50), В (20;30;0), найти его натуральную величину

а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;

б) Находим третью проекцию прямой:

— откладываем значение y по горизонтали с правой стороны от оси z и находим проекции точек согласно фронтальным проекциям точек

в) Находим Н.В.- проводим в π2 из т. В₂ горизонталь h₂;

— полученное расстояние от т. А₂ до h₂ откладываем на перпендикуляре от т. А₁ в π1;

Достроить горизонтальную проекцию многоугольника ABCDK и определить угол наклона плоскости к απ1

а) Рассмотрим π2,проецируем точки плоскоасти АВС DK на проекцию απ2 II оси х₁₂ получаем точки А`<sub>2,</sub> В`_2, С`<sub>2</sub> , D`₂ , K`₂ и проецируем их на ось х₁₂

Построить сечение пирамиды плоскостью α

Построить точку пересечения прямой а с плоскостью α

а) Проводим через прямую а в π1 фронталь f₁

б) f₁ ∩ α π1=1₁, определяем проекцию 1₂ на оси х₁₂

б) из т. 1₂ II α π2 проводим луч, пересекающий прямую а в точке А ₂ – точка пересечения а с плоскостью α

Построить три проекции прямой А (10; 15;50), В (20;30;10), найти его натуральную величину

а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;

б) Находим третью проекцию прямой:

— откладываем значение y по горизонтали с правой стороны от оси z и находим проекции точек согласно фронтальным проекциям точек

в) Находим Н.В.- проводим в π2 из т. В₂ горизонталь h₂;

— полученное расстояние от т. А₂ до h₂ откладываем на перпендикуляре от т. В₁ в π1;

Построить недостающую проекцию треугольника, лежащего в плоскости, заданной параллельными прямыми а и b

г) На проекционных лучах из т. А₂ и С₂ определяем проекции А₁ и С₁ на прямых 3₁1₁ и 2₁4₁

д) А₁ В ₁С₁ – проекция треугольника в π1

Вращением вокруг оси i совместить точку K с плоскостью α

а) II оси х₁₂ в проецируем проекцию т. К на проекцию плоскости απ2 , получаем т. 1₂ находим ее горизонтальную проекцию 1₁

б) В π1 II плоскости απ1из т. 1₁ проводим луч

в) i – ось вращения, вращаем т. К₁,до совмещения ее с лучом из т. 1₁, получаем т. К’₁

г) Находим на пересечении проекционных лучей т К.

Построить линии пересечения цилиндра с конусом

а) Цилиндр и конус в π2 пересекаются в т. 1₂2₂; находим их проекции 1₁2₁

в π1 на горизонтальной оси цилиндра

б) В π2 проводим секущие плоскости II оси х₁₂; данные плоскости пересекают цилиндр и конус; отмечаем радиусы пересечения и проецируем их на плоскость π1 на горизонтальную ось цилиндра и сферы; проводим окружности; пересечение окружностей, образованных сечением одной плоскости, дают точки пересечения сферы и конуса.

в) Соединяем получившиеся точки в π1 и проецируем их на соответствующие секущие плоскости в π2, соединяем линию пересечения

г) Определяем видимость

Построить линию пересечения двух плоскостей, определить видимость линий

а) Рассмотрим π1

г) КМ – линия пересечения

д) Определяем видимость с помощью конкурирующих точек

Построить точку пересечения прямой С с плоскостью, заданной пересекающимися прямыми а и b

а) В плоскости π2через прямую с₂ проводим плоскость α₂, она засекает плоскость (a ∩ b) в точках 1₂2₂, находим их проекции в π1

б) 1₁2₁∩ с₁ =М₂ – точка пересечения прямой с и (a ∩ b)

Построить три проекции прямой А (0; 5;50), В (10;30; 0), найти его натуральную величину

а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;

б) Находим третью проекцию прямой:

— откладываем значение y по горизонтали с правой стороны от оси z и находим проекции точек согласно фронтальным проекциям точек

в) Находим Н.В.- проводим в π2 из т. В₂ горизонталь h₂;

— полученное расстояние от т. А₂ до h₂ откладываем на перпендикуляре от т. В₁ в π1;

Построить недостающую проекцию треугольника, лежащего в плоскости, заданной параллельными прямыми a и b

г) На проекционных лучах из т. А₁ и С₁ определяем проекции А₂ и С₂ на прямых 3₂1₂ и 2₂4₂

д) А₂ В ₂С₂ – проекция треугольника в π2

Преобразовать чертеж так, чтобы отрезок АВ спроецировался в точку (применить способ замены плоскостей проекций)

а) Производим замену плоскости π1 на π4 II А₁ В₁

б) Находим проекции А₄ В₄ согласно высотам в плоскости π2

в) Производим замену плоскости π4 на π5 перпендикулярно отрезку А₄В_4; перпендикулярно оси х₄₅ переносится проекция отрезка, проецирующаяся в точку (расстояния от оси х₄₅ откладываются согласно расстоянию от отрезка до оси х₁₄)

Построить линию пересечения призмы и конуса

а) Рассмотрим π1: находим середины сторон призмы: 1₁, 2₁, 3₁ и их проекции во фронтальной плоскости

б) Продливаем прямые S₁ 3₁; S₁ 2₁;S₁ 1₁ до пересечения с основанием конуса в т. 6 ₁,5₁,4₁ соответственно

г) Определяем точки пересечения данных прямых с проекциями середин отрезков призмы

д) Определяем линию пересечения призмы и конуса

Построить линию пересечения пирамиды с плоскостью

а) В плоскости π1 перпендикулярно h₁ производим замену плоскости проекций π4; сносим проекции точек пирамиды и плоскости (h∩f)

б) Плоскость (h∩f) занимает в π4 проецирующее положение, она пересекает SAВС в точках 2₄ , 3₄ , 4 ₄, 5₄; находим их проекции в π1 и π2

в) Соединяем полученные точки получаем сечение 2₂ 3₂ 4₂ 5 ₂

Построить точку пересечения прямой а с плоскостью α

а) Заключаем прямую a в плоскость β; α∩β=1₂

б) Находим проекцию точки 1 на плоскости π1

в) Проводим прямую а₂ до пересечения с осью х, получаем т. 2₂

г) Находим проекцию т. 2 в плоскости π1

е) Определяем видимость.

Построить три проекции прямой А (40; 5;50), В (20;30; 0), найти его натуральную величину

а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;

б) Находим третью проекцию прямой:

— откладываем значение y по горизонтали с правой стороны от оси z и находим проекции точек согласно фронтальным проекциям точек

в) Находим Н.В.- проводим в π2 из т. В₂ горизонталь h₂;

— полученное расстояние от т. А₂ до h₂ откладываем на перпендикуляре от т. В₁ в π1;

Построить три проекции прямых АВ и CD общего положения, заданных координатами точек: А (20; -30;-10), В (-20;15;30), С (40; -10; 15), D (15;-30;-35)

а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;

б) Каждая точка должна иметь три проекции.

Определить расстояние от т. А до плоскости CDE

а) Проводим в π2 горизонталь h₂ II оси х, замечаем точку 1_2, находим ее проекцию 1₁ в π1, проводим h₁

б) Проводим в π1фронталь f₁ II оси х, замечаем точку 2_1, находим ее проекцию 2₂ в π2, проводим f₂

в) Опускаем перпендикуляр из т. А₂ на f₂

г) Опускаем перпендикуляр из т. А₁ на h₁

д) Заключаем перпендикуляр из т. А₂ в плоскость α₂

е) Плоскость α₂ ∩ (CDE) = 3₂ 4₂, находим их проекции в плоскости π1

ж) Перпендикуляр, опущенный из т. А пересекается с 3₁ 4₁ в т. К₁ , находим проекцию т. К в π2

з) Находим длину АК, для этого в π1 замечаем длину перпендикуляра

А₁ К₁ = L (измерения производить перпендикулярно оси х)

и) В π2 перпендикулярно А₂ К₂ из т. А₂ выводим перпендикуляр и откладываем длину L, получаем т. А₀₂; длина К₂А₀₂ – истинная величина перпендикуляра А К.

Построить через точку А прямую, перпендикулярную прямой b

а) Производим замену плоскости π1 на π4 II b₁

б) Находим проекции b₄ и А₄ согласно высотам в плоскости π2

в) Из т. А₄ опускаем на b₄ перпендикуляр – прямая m ₄

Построить сечение конуса и цилиндра, определить видимость

а) Рассмотрим проекции тел вращения в π2:

— образующая конуса S₂ K₂ пересекает цилиндр в т. 1₂ и 2₂, проецируем точки на горизонтальную ось конуса, проходящую через вершину S, в плоскости π1;

б) В плоскости π2 проводим секущие плоскости α₁, α₂, α₃, α₄, данные плоскости пересекают и конус и цилиндр, находим общие точки пересечения, проецируем их в π1на соответствующие сечения плоскостями

в) Соединяем точки сечения

г) Определяем видимость

Возможно, вас также заинтересует эта ссылка:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Параллельность прямой к плоскостиСкачать

Начертательная геометрия. Инженерная графика. Практикум для студентов вузов (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (45, 10, 5), В (15, 50, 0). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 15 мм и расположенную под углом 45° к плоскости W.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (5, 0, 35), В (55, 10, 5). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 45 мм и расположенную под углом 45° к плоскости W.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (20, 30, 50), В (5, 5, 10). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить фронталь, удаленную от плоскости V на 45 мм и расположенную под углом 35° к плоскости H.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Задача 1. Построить прямую, проходящую через точки А (20, 0, 10), В (5, 35, 50). Определить положение прямой относительно плоскостей проекций. Построить следы прямой.

Задача 2. Построить горизонталь, удаленную от плоскости H на 40 мм и расположенную под углом 15° к плоскости V.

Задача 3. Через точку А провести прямую b, параллельную прямой а.

Задача 4. Через точку А провести прямую b, пересекающую прямую а; а через точку С — прямую m, скрещивающуюся с прямой n.

Задача 5. Определить натуральную величину отрезков АВ и CD и углы наклона их к плоскостям проекций.

Тема 3. ПЛОСКОСТЬ

Цель занятия — научиться:

1) выполнять чертеж плоскости;

2) определять положение плоскости в пространстве относительно плоскостей проекций;

3) строить точку и прямую, принадлежащие плоскости;

4) строить главные линии плоскости;

5) строить точку пересечения прямой и плоскости, определять видимость прямой;

6) строить линию пересечения плоскостей, определять видимость плоскостей.

Плоскость может быть задана следующими способами:

1. Тремя точками, не принадлежащими одной прямой (рис. 10, а).

2. Прямой и точкой, не лежащей на ней (рис. 10, б).

3. Двумя пересекающимися прямыми (рис. 10, в).

4. Двумя параллельными прямыми (рис. 10, г).

5. Плоской геометрической фигурой (рис. 10, д).

След плоскости — прямая, по которой пересекаются плоскость с плоскостями проекций.

Линию пересечения плоскости с горизонтальной плоскостью проекций называют горизонтальным следом плоскости, с фронтальной — фронтальным следом плоскости, с профильной — профильным следом плоскости.

Плоскость может занимать следующие положения относительно плоскостей проекций:

1. Плоскости общего положения — это плоскости не параллельные и не перпендикулярные ни одной из плоскостей проекций.

2. Плоскости частного положения:

а) проецирующие плоскости — плоскости, перпендикулярные к какой-либо плоскости проекций;

б) плоскости уровня — плоскости, параллельные какой-либо плоскости проекций и перпендикулярные к другим двум.

Точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости.

Прямая принадлежит плоскости, если она имеет две общие точки с этой плоскостью.

Главными линиями плоскости являются:

1. Линии уровня плоскости — прямые, принадлежащие заданной плоскости и параллельные какой-либо плоскости проекций:

а) горизонталь плоскости — прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций;

б) фронталь плоскости — прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций;

в) профильная прямая плоскости — прямая, принадлежащая плоскости и параллельная профильной плоскости проекций.

2. Линии наибольшего наклона плоскости — прямые, принадлежащие плоскости и перпендикулярные к ее горизонтали (фронтали, профильной прямой).

Результатом пересечения прямой и плоскости является точка. Для нахождения точки пересечения в общем случае пользуются следующим алгоритмом:

1) заданную прямую заключают в вспомогательную проецирующую плоскость;

2) находят линию пересечения заданной и вспомогательной плоскостей;

3) точка пересечения найденной линии и заданной является искомой.

Результатом пересечения двух плоскостей является прямая, поэтому для ее определения достаточно найти две точки, принадлежащие одновременно каждой из двух заданных плоскостей. В общем случае пользуются следующим алгоритмом:

1) вводят две вспомогательные секущие (проецирующие) плоскости;

2) находят линии пересечения заданных плоскостей с одной из вспомогательных;

3) находят точку пересечения найденных линий пересечения;

4) выполняют те же действия со второй вспомогательной плоскостью;

5) через полученные точки проводят искомую линию пересечения.

Если плоскости заданы следами, то построение их линии пересечения упрощается, т. к. роль вспомогательных секущих плоскостей могут выполнять плоскости проекций.

При определении видимости точек, линий, плоскостей условно считают, что плоскости непрозрачны. Анализ видимости линий проводят путем анализа видимости конкурирующих точек. Конкурирующие точки — это точки, проекции которых на одной из плоскостей проекций совпадают.

При определении видимости на фронтальной плоскости проекций смотрят на конкурирующие точки снизу и определяют, какая точка или линия находится ближе к наблюдателю.

При определении видимости на горизонтальной плоскости проекций смотрят на конкурирующие точки сверху и определяют, какая точка или линия находится выше.

Примеры решения задач

Пример 1. Плоскость задана параллельными прямыми а и в (рис. 11). Построить произвольную прямую, принадлежащую этой плоскости.

Задаем на прямых а и в произвольные точки M и N, через которые проводим прямую MN.

Пример 2. Плоскость α задана следами (рис. 12). Точка А принадлежит данной плоскости?

Плоскость α является плоскостью общего положения. Построим линию уровня плоскости, например, горизонталь h. Проводим через фронтальную проекцию точки А фронтальную проекцию горизонтали параллельно оси x.

h″ ∩ αV = N″. Находим N′: N′ € x. Через точку N′ проводим горизонтальную проекцию горизонтали h′, h′ ║ αH. Таким образом, точка А не принадлежит заданной плоскости α, поскольку она не лежит на прямой, принадлежащей этой плоскости.

Пример 3. На формате А3 по заданным координатам построить комп-лексный чертеж пересечения двух плоскостей. Определить видимость. Выполнить в цвете.

Плоскости ABC и DEF являются плоскостями общего положения (рис. 13). Заключим фронтальную проекцию FD в вспомогательную фронтально-проецирующую плоскость α, которая пересекает треугольник ABC по отрезку 1-2. 1′-2′ ∩ F′D′ = K′. Находим K″.

Введем вторую вспомогательную секущую плоскость β. Заключим горизонтальную проекцию AC в горизонтально-проецирующую плоскость β. β ∩ DEF = 3-4. 3″-4″ ∩ A″C″ = L″. Находим L′.

Точки K и L принадлежат линии пересечения заданных плоскостей, поэтому отрезок KL является искомым.

Видимость линий определяем с помощью конкурирующих точек.

Задания для самостоятельного решения

Задача 1. Построить в трех проекциях чертеж плоскости АВС по заданным координатам: А (70, 10, 65), В (20, 15, 10), С (90, 70, 35). Провести горизонталь плоскости.

Задача 2. Построить недостающий след плоскости α, если точка А принадлежит плоскости.

Задача 3. Достроить недостающую проекцию плоскости, заданной плоской фигурой.

Задача 4. Построить точку пересечения прямой l и плоскости α. Определить видимость прямой.

🎦 Видео

Построение параллельной плоскости на расстояние 30 мм.Скачать

Горизонталь в плоскостиСкачать

Задача 1.1. Прямая и плоскость. Построить комплексный чертеж треугольника АВС и прямой МN.Скачать

Построение проекции пирамиды. Метод прямого треугольника.Скачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Построить недостающую проекцию треугольника АВС, лежащего в плоскости, заданной параллельными прямымСкачать

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

ПРОЕКЦИИ РАВНОСТОРОННЕГО ТРЕУГОЛЛЬНИКА НА П1/П2 и углы наклона его плоскости к плоскостям проекцийСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Линия пересечения плоскостейСкачать

Задача 1.1. Прямая и плоскость. Построить комплексный чертеж треугольника АВС и прямой МN.Скачать

Определение кратчайшей расстоянии от точки до плоскостиСкачать

Угол наклона плоскости общего положения относительно плоскостям проекцииСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Построение следов плоскостиСкачать

Точка встречи прямой с плоскостьюСкачать

Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать