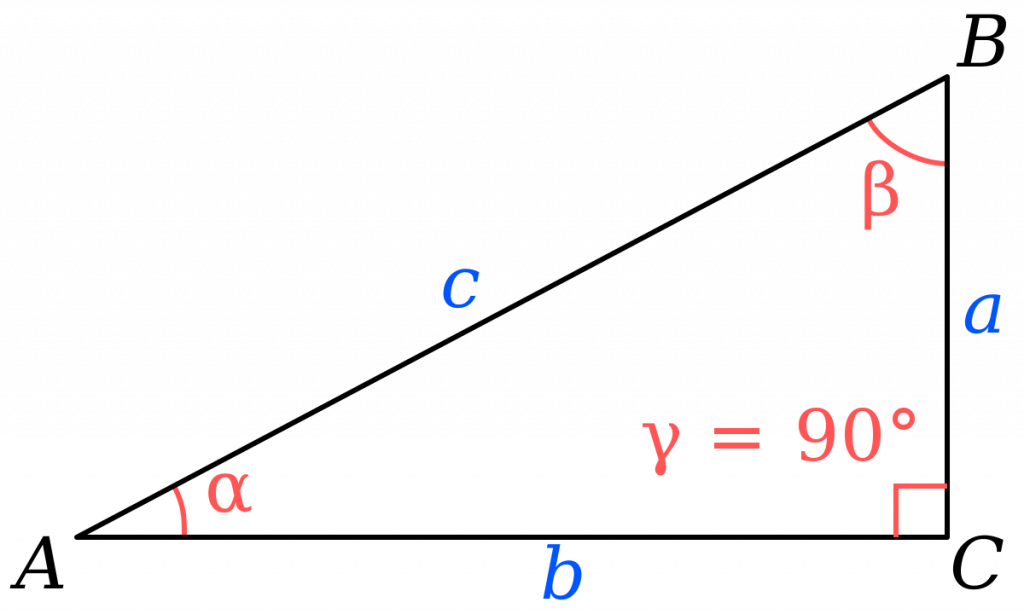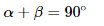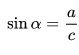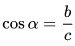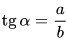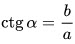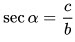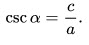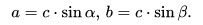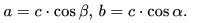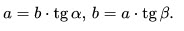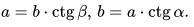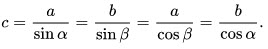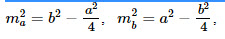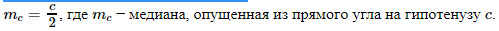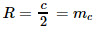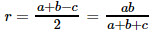Прямоугольный треугольник углы формулы

Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Онлайн калькулятор

Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для угла α:
  • угол β
  • длины катетов a и b
  • длину гипотенузы (с) и длину одного из катетов
• для угла β:
  • угол α
  • длины катетов a и b
  • длину гипотенузы (с) и длину одного из катетов

Введите их в соответствующие поля и получите результат.

Найти угол α зная угол β и наоборот

Формула

Найти углы прямоугольного треугольника зная катеты

Катет a =
Катет b =

Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?

Формулы

Пример

Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:

Найти углы прямоугольного треугольника по катету и гипотенузе

Гипотенуза c =
Катет =

Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?

Видео:Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Все формулы прямоугольного треугольника — примеры расчетов

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Формулы

1. Сумма острых углов прямоугольного треугольника равна 90 0 :

2. Синус острого угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе:

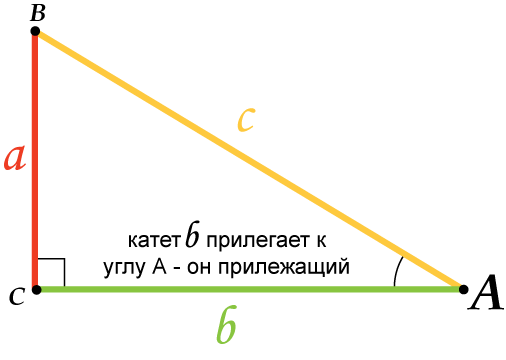
3. Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе:

4. Тангенс острого угла равен отношению противолежащего катета к прилежащему катету:

5. Котангенс острого угла равен отношению прилежащего катета к противолежащему катету:

6. Секанс острого угла равен отношению гипотенузы к прилежащему катету:

7. Косеканс острого угла равен отношению гипотенузы к противолежащему:

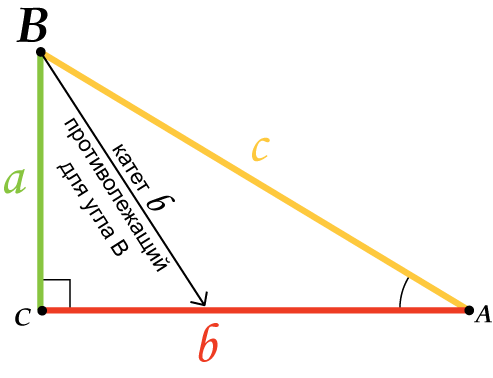
8. Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла:

9. Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла:

10. Катет, противолежащий углу, равен произведению второго катета на тангенс угла:

11. Катет, прилежащий углу, равен произведению второго катета на котангенс угла:

12. Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними):

13. Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

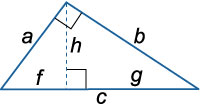
14. Медианы, проведенные к катетам прямоугольного треугольника:

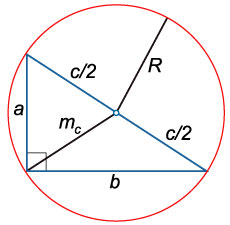
15. Медиана, проведенная к гипотенузе:

16. Радиус окружности, описанной около прямоугольного треугольника:

17. Радиус окружности, вписанной в прямоугольный треугольник:

18. Площадь прямоугольного треугольника равна половине произведения катетов треугольника:

Видео:№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать

Углы прямоугольного треугольника

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Калькулятор расчёта углов прямоугольного треугольника

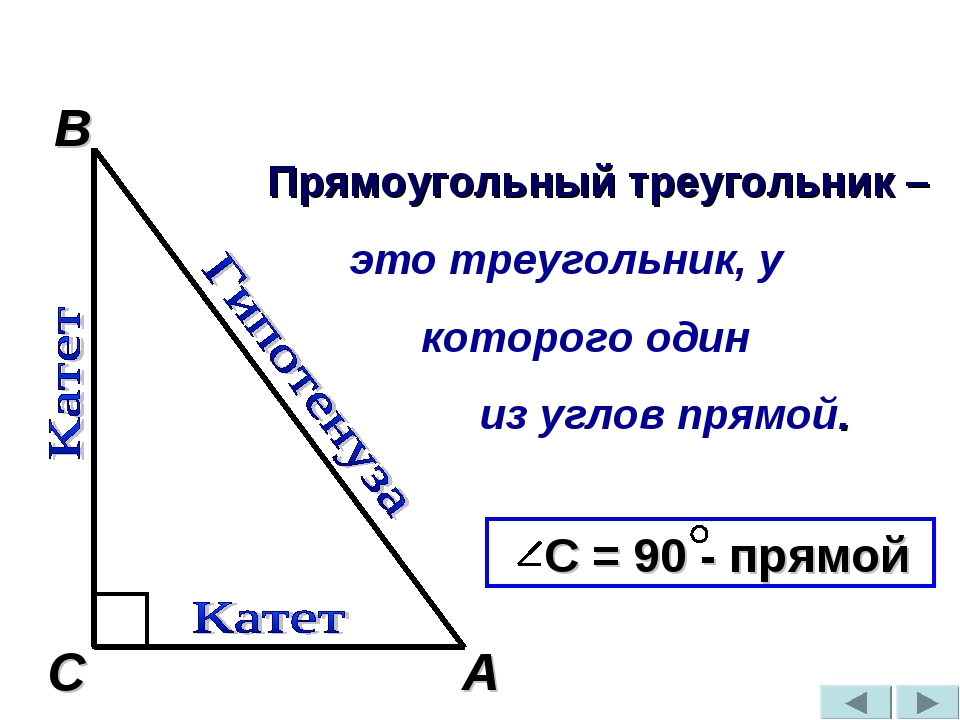
Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).

Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.

Формула тангенса

• tg α — тангенс угла α
• a — противолежащий катет
• b — прилежащий катет

Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x . Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.

Видео:Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18Скачать

Углы треугольника

Сумма углов треугольника всегда равна 180 градусов:

Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.

Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:

Острый угол — угол, значение которого меньше 90°.

У прямоугольного треугольника один угол прямой, а два других угла — острые.

🎥 Видео

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Решение прямоугольных треугольниковСкачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

ТРИГОНОМЕТРИЯ с нуля — Синус, косинус, тангенс и котангенс острого углаСкачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Нахождение стороны прямоугольного треугольникаСкачать

Прямоугольный треугольник Полное досьеСкачать