Построение окружности и прямоугольной диметрии диметрия (8 видео)

Изображение кругов в изометрических и диметрических проекциях

Из геометрии известно, что круг можно рассматривать как правильный многоугольник с большим количеством сторон. Следовательно, изометрическое изображение круга можно строить так же, описывая вокруг него квадрат (рис. 155, а). Точки касания А, В, С и D будут находиться на средине сторон квадрата и легко могут быть нанесены на аксонометрическое изображение (рис. 155, б). Промежуточные точки Е’, F’ и другие находим с помощью их координат. Изометрической проекцией круга является эллипс; его большая ось EG расположена под углом 60° к горизонту по большой диагонали ромба, а малая ось — под углом 30° по малой диагонали ромба.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451018_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Аксонометрические изображения круга чаще строят, проводя оси х и у через центр окружности (рис. 156, а); при этом отпадает надобность в построениях квадрата и ромба. Выбрав точку О’, проводим через нее оси х’ и у’ (рис. 156, б), откладываем на осях величины, равные радиусу окружности, получаем точки А’, В’, С и D’. Другие точки находим с помощью их координат; построение точки Е показано двойными тонкими линиями. Два координатных отрезка для точки Е составляют так называемую координатную ломаную, которая будет в дальнейшем широко применяться при построении точек, расположенных в пространстве. Большая ось эллипса E’G’ для круга, лежащего в плоскости х’О’у’, расположена горизонтально, а малая ось — вертикально.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451012_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

В начертательной геометрии доказывается, что отношение осей эллипса, являющегося изображением окружности, в прямоугольной изометрии равняется 0,58, т. е. если большую ось эллипса d принять за единицу, то малая ось будет равна 0,58d. Это положение иллюстрируем так: расположим плоскость квадрата, в который вписана окружность, параллельно плоскости П₂ (рис. 157, а); повернем квадрат вокруг его горизонтальной диагонали на угол, равный 54° 30′ (рис. 157, б); спроецируем квадрат и окружность на плоскость, параллельную горизонтальной диагонали квадрата (рис. 157, е). Диагональ ромба и горизонтальный диаметр окружности спроецируются при этом в действительную величину, стороны ромба изобразятся прямыми, составляющими =0,82 от величины d; наклоненные диагональ и диаметр окружности спроецируются с искажением и составят 0,58 от своей действительной величины, поскольку sin 35°30′ = 0,58.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451023_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Изображение окружности на рис. 157, в является натуральным. Чтобы перейти к «приведенному» изображению, которое, как известно, увеличено в 1,22 раза, умножим все три величины на указанное количество раз. Получим: сторона ромба 0,82dxl,22 = 1,004d = d; большая ось эллипса dx 1,22 = 1,22d; малая ось эллипса 0,58dx1,22= 0,71d.

Зная эти зависимости, мы можем по заданному диаметру круга быстро найти размеры большой и малой осей эллипса, являющегося изометрической проекцией окружности. Пусть требуется построить прямоугольную изометрию круга, диаметр окружности которого равен 50 мм. Определяем размеры большой и малой осей эллипса: большая ось А’В’ равна 50х X 1,22 = 61 мм, малая ось CD’ равна 50’х0,71=35 мм. Строим по этим размерам оси эллипса на чертеже (рис. 158, а).

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451055_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Из геометрического черчения известно (см. рис. 47), что по осям эллипса можно построить его кривую. Практически эллипс в изометрии обычно заменяют овалом, который строят следующим образом (рис. 158, б). На большой А’В’ и малой CD’ осях строим две окружности; они пересекают продолжение малой оси в точках 1 и 2, а большую ось — в точках 3 и 4; эти точки являются центрами для дуг овала; используя их, вычерчиваем овал с радиусами r = О’В’—О’С и R = CD’ + г. Точку сопряжения дуг радиусов R и г находим, соединяя точки 1 и 4 прямой и продолжая эту прямую до пересечения с дугами в точке 5.

В прямоугольной изометрии все три эллипса одинаковы по форме, равны друг другу и лишь расположены различно. В отличие от этого в прямоугольной диметрии имеются две различные формы эллипса: одна для плоскости х’О’z’, а другая — для плоскостей х’О’у’ и z’O’y’.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451008_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

Пусть требуется построить прямоугольную диметрию окружности, лежащей в плоскости хОz (рис. 159, а). Описываем вокруг окружности квадрат и проводим его диагонали. Отмечаем точки пересечения диагоналей с окружностью и координатные отрезки, нужные для построения точек Е, F и др. Строим квадрат в прямоугольной диметрии (рис. 159, б), проводим его средние линии А’С и B’D’ и диагонали. Пользуясь координатными отрезками (помечены на чертежах тонкими двойными линиями), находим точки Е’, F’, G’ и H’. Большая ось эллипса F’G’ в прямоугольной диметрии будет равна l,06d, малая ось Е’Н’ будет равна 0,95d (отношение 9 : 10). Полученные восемь точек соединяем от руки, а затем обводим по лекалу. Если требуется более точное построение, то находят с помощью координатных ломаных еще ряд промежуточных точек.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284451062_image-circles-in-isometric-and-dimetric.jpg|—>TEnd—>

В практике эллипс нередко заменяют овалом (рис. 160, а). Центры дуг для построения овала находим так: строим ромб, его средние линии и диагонали, Из центра О’ радиусом r=d/7 проводим вспомогательную окружность.

Она пересекает малую диагональ ромба в точках 1 и 2; используем эти центры для проведения дуг А’В’ и CD’. Соединяем точки А’ и I, С и 2; эти линии пересекают большую диагональ в точках 3 и 4. Пользуясь этими центрами, проводим дуги A’D’ и В’С. При этом способе также не требуется откладывать размеры большой и малой осей; они получаются сами собой при проведении дуг.

Если требуется построить прямоугольную диметрию окружности, лежащей в плоскости х’О’у’, то на осях х’ и у’ строим параллелограмм и намечаем средние точки его сторон (рис. 160, б). Затем через точку О’ проводим горизонтальную прямую — направление большой оси эллипса. Откладываем на этой прямой размер большой оси эллипса, равный 1,06d. Перпендикулярно к ней проводим малую ось эллипса, размер которой равен 0,35d (отношение 3 : 10). Таким путем получаем восемь точек, принадлежащих эллипсу. В практике избегают построения параллелограмма и строят вместо эллипса овал по его осям А’В’ и CD’ (рис. 160, в). Последовательность построения такая: от центра О’ на продолжении малой оси эллипса откладываем величину большой оси А’В’; получаем точку 1 — центр верхней дуги радиуса R. Тем же радиусом из точки 2 (не показана на чертеже) проводим нижнюю дугу овала. Слева и справа овал дочерчиваем кривыми радиуса r, величину которого принимаем равным r=O’C’/2 Центры 3 и 4 находим, делая засечки дугами r из точек А’ и В’. Точку сопряжения 5 находим, соединяя прямой точки I и 4 и продолжая эту прямую до пересечения с дугой.

Окружность, находящаяся в плоскости, параллельной фронтальной плоскости проекций, проецируется на нее во фронтальной изометрической проекции в виде окружности (рис. 161, а), а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, — в эллипсы, большие оси которых наклонены к осям х’ и z’ под углами 22° 30′. Большие оси эллипсов равны 1,3 диаметра окружности, малые — 0,54 диаметра окружности.

Пусть требуется построить во фронтальной изометрии окружность диаметра 40 мм, находящуюся в плоскости х’О’у’. Определяем большую и малую оси эллипса. Большая ось А’В’ = 1,3d = 1,3 40 = 52 мм, малая ось CD’ = 0,54d = 0,54-40 = 21,6 мм. Овал, заменяющий собой эллипс, удобно строить из четырех центров радиусами, равными R = 1,3d и r = = 0,16d (рис. 161, б). В нашем примере R — 52 мм, г = 0,16d = 6,4 мм. Точка 5 — точка сопряжения.

Окружность, находящаяся в плоскости, параллельной горизонтальной плоскости проекций, проецируется на нее в горизонтальной изометрической проекции в виде окружности (рис. 161, б), а окружности, находящиеся в плоскостях, параллельных фронтальной и профильной плоскостям проекций, — в эллипсы. Большая ось эллипса, параллельного плоскости ?’?’z’, наклонена к оси z’ под углом 15° и равна l,37d; малая ось равна 0,37d. Большая ось эллипса, параллельного плоскости z’О’у’, наклонена к оси у’ под углом 30° и равна 1,22d; малая ось равна 0,71d (так же, как в прямоугольной изометрической проекции).

Видео:Построение эллипса по восьми точкам в прямоугольной диметрииСкачать

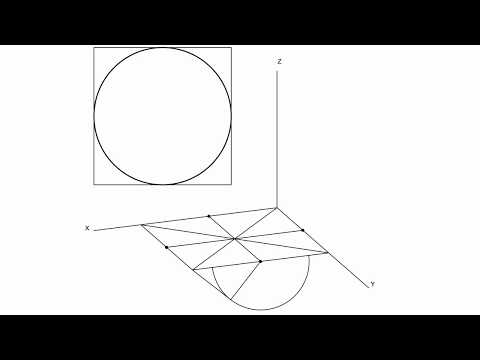
Построение окружности и прямоугольной диметрии диметрия

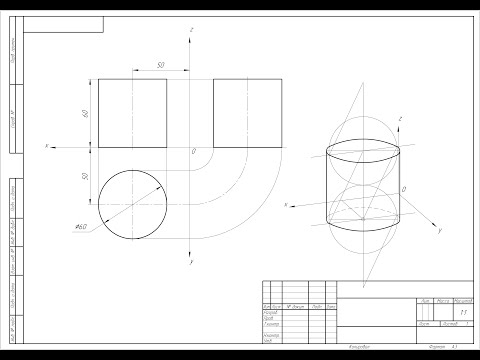
Контрольные задания по теме: эпюр № 6

Для наглядного изображения предметов (изделий или их составных частей) рекомендуется применять аксонометрические проекции, выбирая в каждом отдельном случае наиболее подходящую из них.

Сущность метода аксонометрического проецирования заключается в том, что заданный предмет вместе с координатной системой, к которой он отнесен в пространстве, параллельным пучком лучей проецируется на некоторую плоскость. Направление проецирования на аксонометрическую плоскость не совпадает ни с одной из координатных осей и не параллельно ни одной из координатных плоскостей.

Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям. Под коэффициентом искажения понимается отношение величины изображения в аксонометрической проекции к величине изображения в ортогональной проекции.

В зависимости от соотношения коэффициентов искажения аксонометрические проекции подразделяются на:

— изометрические, когда все три коэффициента искажения одинаковы (k_x=k_y=k_z);

— диметрические, когда коэффициенты искажения одинаковы по двум осям, а третий не равен им (k_x= k_z ≠k_y);

— триметрические, когда все три коэффициенты искажения не равны между собой (k_x≠k_y≠k_z).

В зависимости от направления проецирующих лучей аксонометрические проекции подразделяются на прямоугольные и косоугольные. Если проецирующие лучи перпендикулярны аксонометрической плоскости проекций, то такая проекция называется прямоугольной. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая. Если проецирующие лучи направлены под углом к аксонометрической плоскости проекций, то такая проекция называется косоугольной. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

В прямоугольной изометрии углы между осями равны 120°. Действительный коэффициент искажения по аксонометрическим осям равен 0,82, но на практике для удобства построения показатель принимают равным 1. Вследствие этого аксонометрическое изображение получается увеличенным в 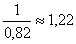раза.

Изометрические оси изображены на рисунке 57.

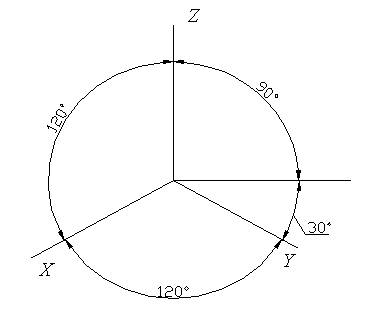
Рисунок 57

Построение изометрических осей можно выполнить при помощи циркуля (рисунок 58). Для этого сначала проводят горизонтальную линию и перпендикулярно к ней проводят ось Z. Из точки пересечения оси Z с горизонтальной линией (точка О) проводят вспомогательную окружность произвольным радиусом, которая пересекает ось Z в точке А. Из точки А этим же радиусом проводят вторую окружность до пересечения с первой в точках В и С. Полученную точку В соединяют с точкой О — получают направление оси Х. Таким же образом соединяют точку С с точкой О — получают направление оси Y.

Рисунок 58

Построение изометрической проекции шестиугольника представлено на рисунке 59. Для этого необходимо отложить по оси X радиус описанной окружности шестиугольника в обе стороны относительно начала координат. Затем, по оси Y отложить величину размера под ключ, из полученных точек провести линии параллельно оси X и отложить по ним величину стороны шестиугольника.

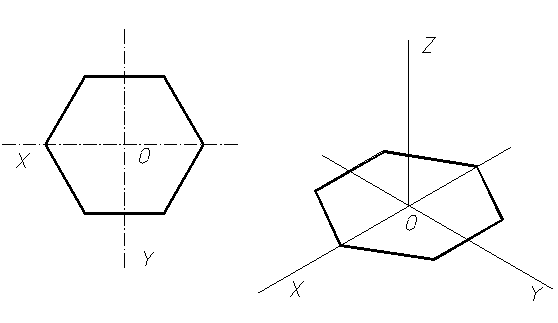
Рисунок 59

Построение окружности в прямоугольной изометрической проекции

Наиболее сложной плоской фигурой для вычерчивания в аксонометрии является окружность. Как известно, окружность в изометрии проецируется в эллипс, но построение эллипса довольно сложно, поэтому ГОСТ 2.317-69 рекомендует вместо эллипсов применять овалы. Существует несколько способов построения изометрических овалов. Рассмотрим один из наиболее распространенных.

Размер большой оси эллипса 1,22d, малой 0,7d, где d — диаметр той окружности, изометрия которой строится. На рисунке 60 показан графический способ определения большой и малой осей изометрического эллипса. Для определения малой оси эллипса соединяют точки С и D. Из точек С и D, как из центров, проводят дуги радиусов, равных СD, до взаимного их пересечения. Отрезок АВ — большая ось эллипса.

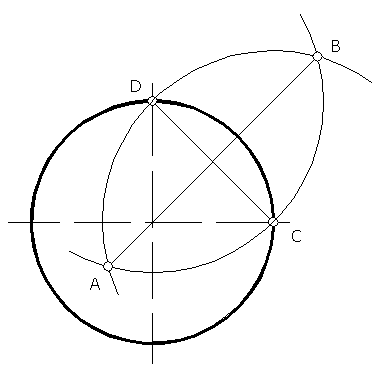
Рисунок 60

Установив направление большой и малой осей овала в зависимости от того, какой координатной плоскости принадлежит окружность, по размерам большой и малой оси проводят две концентрические окружности, в пересечении которых с осями намечают точки О₁, О₂, О₃, О₄, являющиеся центрами дуг овала (рисунок 61).

Для определения точек сопряжения проводят линии центров, соединяя О₁, О₂, О₃, О₄. из полученных центров О₁, О₂, О₃, О₄ проводят дуги радиусами R и R₁. размеры радиусов видны на чертеже.

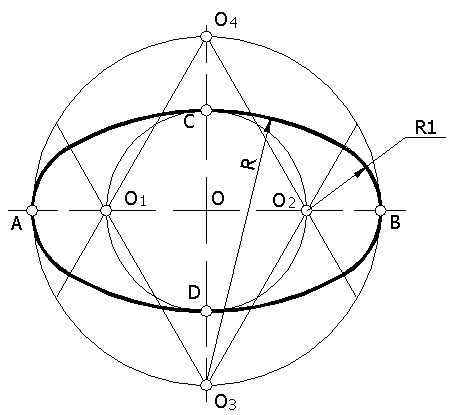
Рисунок 61

Направление осей эллипса или овала зависит от положения проецируемой окружности. Существует следующее правило: большая ось эллипса всегда перпендикулярна к той аксонометрической оси, которая на данную плоскость проецируется в точку, а малая ось совпадает с направлением этой оси (рисунок 62).

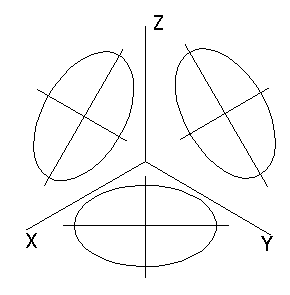
Рисунок 62

Штриховка и изометрической проекции

Линии штриховки сечений в изометрической проекции, согласно ГОСТ 2.317-69, должны иметь направление, параллельное или только большим диагоналям квадрата, или только малым.

Прямоугольной диметрией называется аксонометрическая проекция с равными показателями искажения по двум осям X и Z, а по оси Y показатель искажения в два раза меньше.

По ГОСТ 2.317-69 применяют в прямоугольной диметрии ось Z, расположенную вертикально, ось Х наклонную под углом 7°, а ось Y-под углом 41° к линии горизонта. Показатели искажения по осям X и Z равны 0,94, а по оси Y-0,47. Обычно применяют приведенные коэффициенты k_x=k_z=1, k_y=0,5, т.е. по осям X и Z или по направлениям им параллельным, откладывают действительные размеры, а по оси Y размеры уменьшают в два раза.

Для построения осей диметрии пользуются способом, указанным на рисунке 63, который заключается в следующем:

На горизонтальной прямой, проходящей через точку О, откладывают в обе стороны восемь равных произвольных отрезков. Из конечных точек этих отрезков вниз по вертикали откладывают слева один такой же отрезок, а справа – семь. Полученные точки соединяют с точкой О и получают направление аксонометрических осей X и Y в прямоугольной диметрии.

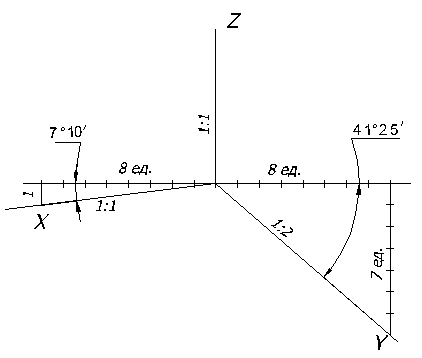
Рисунок 63

Построение диметрической проекции шестиугольника

Рассмотрим построение в диметрии правильного шестиугольника, расположенного в плоскости П₁ (рисунок 64).

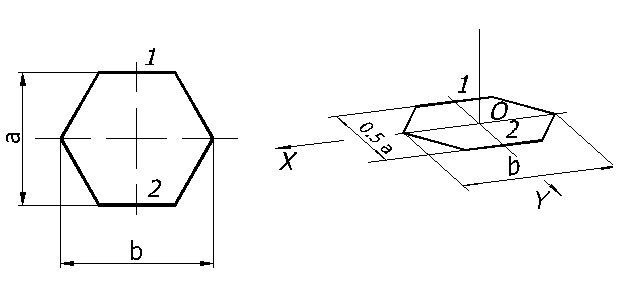
Рисунок 64

На оси Х откладываем отрезок равный величине b, чтобы его середина находилась в точке О, а по оси Y – отрезок а, размер которого уменьшен вдвое. Через полученные точки 1 и 2 проводим прямые параллельно оси ОХ, на которых откладываем отрезки равные стороне шестиугольника в натуральную величину с серединой в точках 1 и 2. Полученные вершины соединяем. На рисунке 65а изображен в диметрии шестиугольник, расположенный параллельно фронтальной плоскости, а на рисунке 66б -параллельно профильной плоскости проекции.

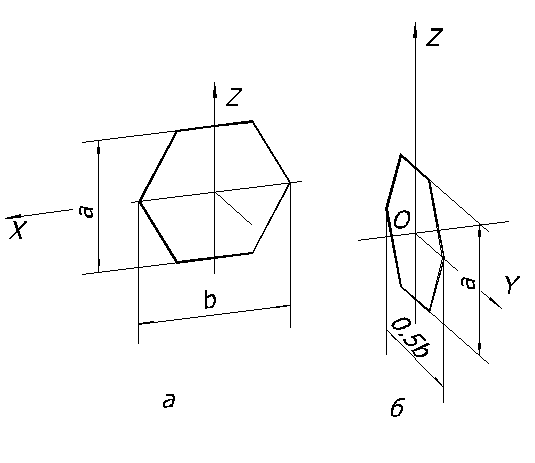
Рисунок 65

Построение окружности в диметрии

В прямоугольной диметрии все окружности изображаются эллипсами,

Длина большой оси для всех эллипсов одинакова и равна 1,06d. Величина малой оси различна: для фронтальной плоскости равна 0,95d , для горизонтальной и профильной плоскостей – 0,35 d.

На практике эллипс заменяется четырехцентровым овалом. Рассмотрим построение овала, заменяющего проекцию окружности, лежащей в горизонтальной и профильной плоскостях (рисунок 66).

Через точку О – начало аксонометрических осей, проводим две взаимно перпендикулярные прямые и откладываем на горизонтальной линии величину большой оси АВ=1,06d , а на вертикальной линии величину малой оси СD=0,35d. Вверх и вниз от О по вертикали откладываем отрезки ОО₁ и ОО₂, равные по величине 1,06d. Точки О₁ и О₂ являются центром больших дуг овала. Для определения еще двух центров (О₃ и О₄) откладываем на горизонтальной прямой от точек А и В отрезки АО₃ и ВО₄, равные ¼ величины малой оси эллипса, то есть d.

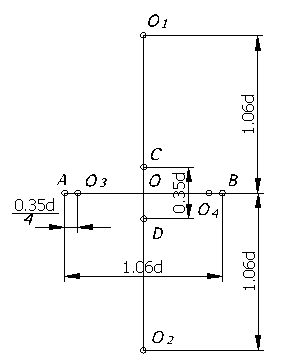
Рисунок 66

Затем, из точек О1 и О2 проводим дуги, радиус которых равен расстоянию до точек С и D, а из точек О3 и О4 – радиусом до точек А и В (рисунок 67).

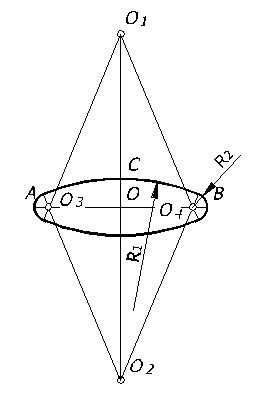
Рисунок 67

Построение овала, заменяющего эллипс, от окружности, расположенной в плоскости П₂, рассмотрим на рисунке 68. Проводим оси диметрии: Х, Y, Z. Малая ось эллипса совпадает с направлением оси Y, а большая перпендикулярна к ней. На осях Х и Z от начала откладываем величину радиуса окружности и получаем точки M, N, K, L, являющиеся точками сопряжения дуг овала. Из точек M и N проводим горизонтальные прямые, которые в пересечении с осью Y и перпендикуляром к ней дают точки О₁, О_2, О_3, О₄ – центры дуг овала (рисунок 68).

Из центров О₃ и О₄ описывают дугу радиусом R₂=О₃ М, а из центров О₁ и О₂ — дуги радиусом R₁= О₂ N

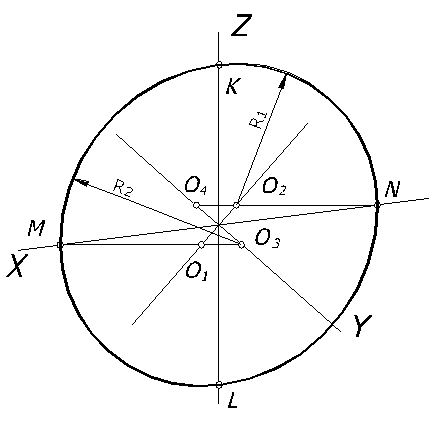
Рисунок 68

Штриховка а прямоугольной диметрии

Линии штриховки разрезов и сечений в аксонометрических проекциях выполняются параллельно одной из диагоналей квадрата, стороны которого расположены в соответствующих плоскостях параллельно аксонометрическим осям (рисунок 69).

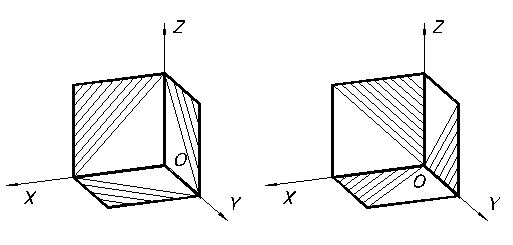
Рисунок 69

Какие виды аксонометрических проекций вы знаете?
Под каким углом расположены оси в изометрии?
Какую фигуру представляет изометрическая проекция окружности?
Как расположена большая ось эллипса для окружности, принадлежащей профильной плоскости проекций?
Какие приняты коэффициенты искажения по осям X, Y, Z для построения диметрической проекции?
Под какими углами расположены оси в диметрии?
Какой фигурой будет являться диметрическая проекция квадрата?
Как построить диметрическую проекцию окружности, расположенной во фронтальной проскости проекций?
Основные правила нанесения штриховки в аксонометрических проекциях.

Тема 12

Наверх

Заключение

Видео:Прямоугольные диметрические проекцииСкачать

Прямоугольная диметрическая проекция

В прямоугольной диметрии ось z расположена вертикально, ось х — под углом 7° 10′, а ось у — под углом 41°25′ к горизонтальной прямой (рис. 4.18). Все отрезки прямых линий геометрического объекта, которые параллельны осям х, у и z на комплексном чертеже, останутся параллельными соответствующим осям в диметрической проекции.

Длины ребер куба на изображении, отложенные в направлении осей х и z, сокращаются до 0,94 действительной длины, а в направлении оси у — до 0,47 действительной длины (рис. 4.19).

Построение диметрической проекции точки (рис. 4.20). Сначала строим оси, как показано на рис. 4.18. Откладываем от точки О

(начала координат) последовательно отрезки на одной из осей и параллельные двум другим осям, получаем точку А.

При построении прямоугольной диметрии координатной ломаной линии следует учитывать, что коэффициент искажения по координатным осям х и z (рис. 4.19) К_х0 = K_z0 = 0,94 принимают равным единице (К_х0 = K_z0 = 1), а по оси у коэффициент искажения К_у0 = 0,47 принимают равным 0,5 (К_);0 = 0,47).

Линии штриховки сечений в прямоугольной диметрической проекции наносят (как показано на рис. 4.21) параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям («спроецированная» штриховка).

На рис. 4.22 показано изображение трехгранной призмы в прямоугольной диметрии. Если ребра призмы параллельны оси х или z, то размер высоты не меняется, но искажается форма основания. При расположении ребер параллельно оси у, высота призмы сокращается вдвое.

Прямоугольная диметрическая проекция окружности. Если построить диметрическую проекцию куба, в грани которого вписаны окружности диаметра D‘ (рис. 4.23, а), то квадратные грани куба будут изображаться в виде параллелограммов, а окружности — в виде эллипсов (рис. 4.23, б). Для построения диметрической проекции окружности (эллипса), расположенной в плоскости, параллельной фронтальной плоскости проекций, надо разделить половину большой диагонали ромба на 10 равных частей. Эллипс должен пройти через точку 3. Проведя через полученную точку 3 две прямые, параллельные осям х и z, на пересечении с малой диагональю ромба получим еще две точки 3, принадлежащие эллипсу. Далее, проводя прямые, параллельные осям до пересечения с диагоналями параллелограммов, получаем точки 3 на остальных гранях куба.

Кроме точек 3 имеются еще четыре точки, через которые проходит эллипс. Эти точки расположены на серединах сторон параллелограммов (например, точка п). Найденные точки эллипсов соединяют кривой по лекалу.

Окружности в прямоугольной диметрической проекции изображают в виде эллипсов. Большая ось эллипсов во всех случаях равна 1,06D где D’ — диаметр окружности. Малые оси эллипсов, расположенных на гранях куба, параллельных горизонтальной и профильной плоскостям проекций, равны 0,3 5D а на грани, параллельной фронтальной плоскости, — 0,9 5D’ (рис. 4.24). Большие оси эллипсов всегда перпендикулярны соответствующим координатным осям, а малые им параллельны.

На рис. 4.25, 4.27 и 4.29 показаны поверхности вращения, выполненные в диметрии с эллипсами, расположенными параллельно горизонтальной плоскости проекций (рис. 4.25), фронтальной плоскости проекций (рис. 4.27), профильной плоскости проекций (рис. 4.29).

В учебных чертежах для упрощения построения диметрических проекций окружности вместо эллипсов рекомендуется применять овалы, очерченные дугами окружностей. Упрощенный способ построения диметрических овалов приведен на рис. 4.26, 4.28, 4.30.

Для построения диметрического овала в плоскости, параллельной горизонтальной плоскости проекций (рис. 4.26), через точку О проводят оси х и z, как показано на рис. 4.18, а также большую ось овала АВ перпендикулярно малой оси CD, принадлежащей оси z. Из центра О, диаметром D_ь равным действительной величине диаметра изображаемой окружности, проводят вспомогательную окружность и на оси х получают точки 7 и 2. Симметричным переносом относительно большой оси овала ЛВ получают точки 3 и 4.

На оси z вверх и вниз от центра О откладывают отрезки, равные диаметру вспомогательной окружности D_h и получают точки 0 и 0 — центры радиусов R. Соединив полученные точки 0 и 0 с точками 7 и 2 соответственно, получают точки 0₂ и 0_{2 — центры радиусов R. Из центров 0 и 0 проводят дуги 14 и 32 радиусом R. Из центров 0₂}и 0₂ проводят дуги 13 и 24 радиусом R].

Для построения овала в плоскости, параллельной фронтальной плоскости проекций (рис. 4.28), проводят оси овалах иz, как показано на рис. 4.18.

Из точки пересечения осей О проводят вспомогательную окружность диаметром D_h равным действительной величине диаметра изображаемой окружности, и находят точки 7,2, 3, 4 — точки пересечения этой окружности с аксонометрическими осями х и z. Из точек 7 и 3 по направлению стрелок проводят горизонтальные линии до пересечения с осями АВ и CD и получают точки 0₂, 0₃, 0₄. Из центров 0 и 0₄ проводят дуги 72 и 34 радиусом R. Из центров 0₂ и 0₂ проводят дуги 14 и 23 радиусом R.

На рис. 4.30 показано упрощенное построение диметрической проекции окружности, расположенной в плоскости, параллельной профильной плоскости проекций. Построение аналогично построению диметрического овала окружности, расположенной в плоскости, параллельной горизонтальной плоскости проекций, разница лишь в том, что большую ось овала ЛВ располагают перпендикулярно малой оси CD, принадлежащей оси х.

На рис. 4.31 приведен пример построения прямоугольной диметрической проекции детали.

Необходимо отметить, что при помощи аксонометрических проекций имеется возможность решать как позиционные, так и метрические задачи.

Отметим, что в инженерной практике (в частности в машиностроении) наибольшее распространение нашли прямоугольные изометрические и диметрические проекции.