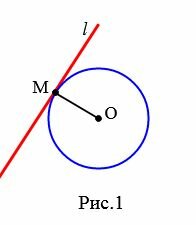
Определение 1. Прямая, которая имеет с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
На рисунке 1 прямая l является касательной к окружности с центром O, а точка M является точкой касания прямой и окружности.
 |
Видео:Построение касательной к окружности из заданной точки. Урок 10. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
Свойство касательной
Теорема 1 (Теорема о свойстве касательной). Касательная к окружности перпендикулярна к радиусу, проведенному из центра окружности к точке касания прямой и окружности.
Доказательство. Пусть l касательная к окружности с центром O и M − точка касания прямой и окружности (Рис.1). Докажем, что ( small l ⊥ OM .)
Предположим, что радиус OM является наклонной к прямой l. Поскольку перпендикуляр, проведенной из точки O к прямой l меньше наклонной OM, от центра окружности до прямой l меньше радиуса окружности. Тогда прямая l и окружность имеют две общие точки (см. статью Взаимное расположение прямой и окружности). Но касательная не может иметь с окружностью две общие точки. Получили противоречие. Следовательно прямая l пенрпендикулярна к радиусу OM.
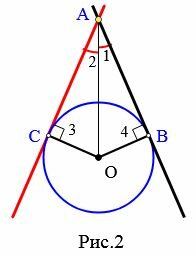
Рассмотрим две касательные к окружности с центром O, которые проходят через точку A и касаются окружности в точках B и C (Рис.2). Отрезки AB и AC называются отрезками касательных, проведенных из точки A.
 |
Теорема 2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через данную точку и центр окружности.
Доказательство. Рассмотрим рисунок 2. По теореме 1 касательные AC и AB перпендикулярны радиусам OC и OB, соответственно. Тогда углы 3 и 4 прямые, а треугольники ACO и ABO, прямоугольные. Эти треугольники равны по катету (OC=OB) и гипотенузе (сторона AO− общая) (подробнее см. в статье Прямоугольный треугольник. Онлайн калькулятор). Тогда AB=AC и ( small angle 1=angle 2 .) Что и требовалось доказать.
Видео:Построение касательной к окружности.Скачать
Теорема, обратная теореме о свойстве касательной
Теорема 3. Если прямая проходит через конец радиуса, лежащей на окружности и перпенжикулярна к этому радиусу, то эта прямая является касательной.
Доказательство. По условию теоремы данный радиус является перпендикуляром от центра окружности к данной прямой. То есть расстояние от центра окружности до прямой равно радиусу окружности, и, следовательно, прямая и окружность имеют только одну общую точку (теорема 2 статьи Взаимное расположение прямой и окружности). Но это означает, что данная прямая является касательной к окружности (Определение 1).
Видео:Строим касательную к окружности (Задача 3).Скачать
Построение касательной к окружности
Задача 1. Через точку M окружности с центром O провести касательную этой окружности (Рис.3).
  |
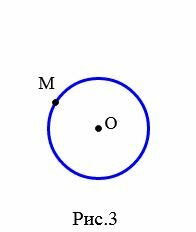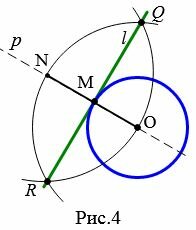Решение. Проведем прямую p через точки O и M. На прямой p из точки M отложим отрезок MN равной OM. Построим две окружности с центрами O и N и одинаковыми радиусами ON. Через точки пересечения этих окружностей проведем прямую l. Полученная прямая является касательным к окружности с центром O и радиусом OM.
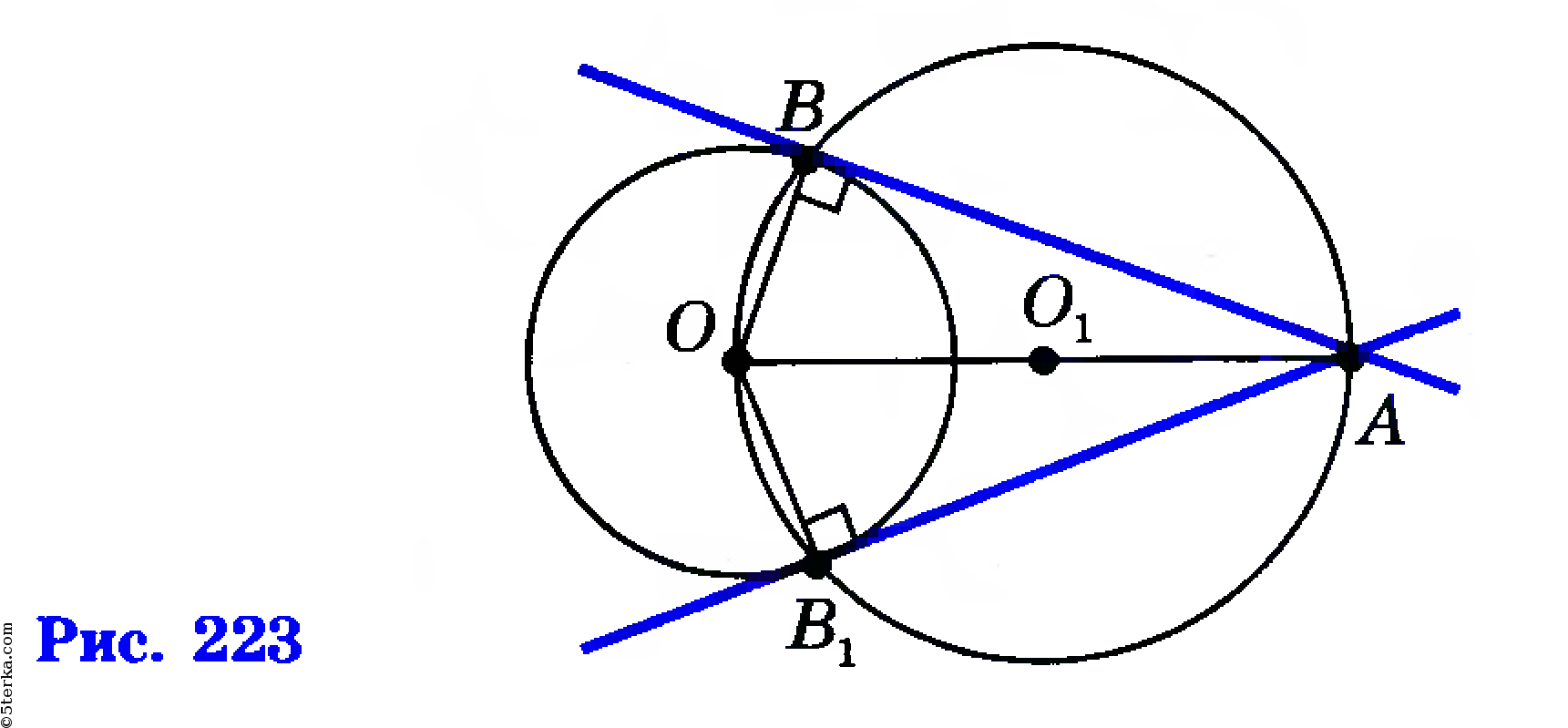
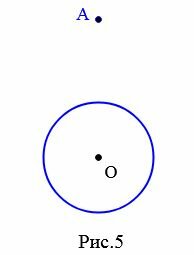
Задача 2. Через точку A не принадлежащая к окружности с центром O провести касательную этой окружности (Рис.5).
  |
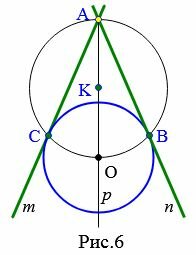Решение. Проведем прямую p через точки O и A (Рис.6). Найдем среднюю точку отрезка OA и обозначим буквой K. Постоим окружность с центром K радиусом KO=KA. Найдем точки пересечения этой окружности с окружностью с центром O. Получим точки B и C. Через точки A и C проведем прямую m. Через точки A и B проведем прямую n. Прямые m и n являются касательными к окружности с центром O.
Видео:ЗАДАЧИ НА ПОСТРОЕНИЕ. §22 геометрия 7 классСкачать
Восемь способов построения касательной к окружности
Государственное бюджетное образовательное учреждение
Проектная работа по геометрии.
Восемь способов построения касательной к окружности.
9 биолого-химический класс
заместитель директора по учебной работе,
Высшее проявление духа – это разум.
Высшее проявление разума – это геометрия.
Клетка геометрии – треугольник. Он так же
неисчерпаем, как и вселенная. Окружность – душа геометрии.
Познайте окружность, и вы не только познаете душу
геометрии, но и возвысите душу свою.
Построить касательную к окружности с центром О и радиусом R, проходящую через точку А, лежащую вне окружности
Построения касательной к окружности, не требующие обоснования, опирающегося на теорию параллельных прямых.
Построение №1.
1. Проведу отрезок ОА
2. Найду К – середину ОА
3. Построю окружность (К; КА).
4. Отмечу точки пересечения окружности (О; r) и окружности (К; КА) С и В.
5. Проведу АВ и ОВ.
Треугольник ОВА – прямоугольный, так как он вписан в окружность, и гипотенуза совпадает с диаметром окружности (К; КА). Следовательно, 
АВО =90°. Для окружности (О; r) ОВ – радиус. ОВ 
АВ, следовательно, АВ – касательная по признаку касательной.
Аналогично, АС – касательная к окружности.
Построение № 1 основывается на факте, который гласит, что касательная окружности перпендикулярна радиусу, проведенному в точку касания.
Для прямой имеется лишь одна точка касания с окружностью.
Через данную на прямой точку можно провести лишь одну перпендикулярную прямую.
1. Построю окружность (А; АО)
2. Построю окружность (О; 2R)
3. Построенные окружности пересекаются в точках М и N.
4. Отрезки ОМ и ОN пересекают данную окружность (О;R) в точках С и В.
5. АВ и АС – искомые касательные.
1. Проведу АО – радиус окружности (А;АО)
АМ и AN также радиусы окружности (А;АО), следовательно
2. ОВ = ВМ = ОС = CN = 0,5OM= 0,5ON, так как ОМ – радиус окружности (O;2R), а ОС – радиус окружности (О;R)
3. Рассмотрим треугольник ОАМ. В нем АМ=ОА, тогда Δ ОАМ равнобедренный по определению. ОВ= ВМ, следовательно, АВ – медиана и высота ΔОАМ, по свойству равнобедренного треугольника.
4. Так как в ΔОАМ АВ – высота, следовательно, АВО = 90°
5. ОВ – радиус, АВО = 90°, следовательно, АВ – касательная по признаку.
6. Аналогично в равнобедренном треугольнике AON АС – касательная (АСО = 90°, ОС – радиус)
7. Итак, АВ и АС – касательные
1. Построю концентрические окружности (О; r) и (O; OA)
2. Проведу ОА; ОА пересекает окружность (О; r) в точке Р.
3. Проведу перпендикуляр МN к радиусу ОА в точке Р.
4. MN пересекает окружность(О; ОА) в точках М и N.
5. Проведу ОМ и ОN. Эти отрезки пересекают окружность (О; r) в точках В и С соответственно.
6. АВ и АС– искомые касательные.
1. ОМ =ОА т. к. радиусы
2. В треугольниках ОМР и ОВА:
ОР = ОВ как радиусы, ОМ = ОА как радиусы, следовательно, ΔОМР = ΔОВА по двум сторонам и углу между ними.
3. Следовательно ОРМ =ОВА= 90° ( как соответствующие углы в равных треугольниках), следовательно, АВ – касательная по признаку касательной.
4. Аналогично, АС – касательная
1. Построю окружность (О, 2r).
2. Построю произвольную касательную к окружности (О; r), пересекающую окружность (О, 2r) в точках M и N.
3. Рассмотрим поворот относительно точки О на угол АОМ, равный α.
4. Точку М надо повернуть на угол α, следовательно она перейдет точку А
Точку М надо повернуть на (180 — α) следовательно, точка М перейдет в точку К.
Тогда, так как угол α остается тем же, AD и АК – касательные по признаку
Построения касательной к окружности одной линейкой, одним циркулем.
1. Прямая ОА пересекает окружность (О, r) в точках Р и Q.
2. Проведу через точку А произвольную прямую, пересекающую окружность(О, r) в точках М и N.
3. Прямая PN пересекает прямую QM в точке L.
4. Прямая PM пересекает прямую QN в точке K.
5. Прямая KL пересекает окружность в точках B и С.
6. АВ и ВС – искомые касательные.
1. Т. к. треугольники PQN и PQM вписаны в окружность и сторона PQ является диаметром окружности, то эти треугольники прямоугольные.
2. В треугольнике PQL отрезки PM и QN – высоты, пересекающиеся в точке К, поэтому KL – третья высота. Тогда KL PQ.
3. Пусть DPK=α, DQK=β. Тогда ctg α : ctg β= |PD|:|DQ| (1).
Построю перпендикуляр к прямой АР в точке А, пересекающий прямую РМ в точке S. Тогда |PA|=|AS|ctg α и |AQ|=|AS|ctg AQS.
4. Так как AQS =AMS = 180° — PMN = PQN = β, то |AQ| = |AS|ctg β. Поэтому |PA| : |AQ| = ctg α : ctg β (2).
5. Сопоставляя (1) и (2) получу |PD| : |PA| = |DQ| : |AQ|, или
После раскрытия скобок и упрощений нахожу, что |OD|·|OA|=R².
5. Из соотношения |OD|·|OA|=R² следует, что |OD|:R=R: |OA|, то есть треугольники ODB и OBA подобны. Поскольку ODB= 90°, то OBA=90°.Следовательно, прямая АВ – искомая касательная, что и требовалось доказать.
Построение № 6. 
1. Прострою окружность (A; |OA|).
2. Найду раствор циркуля, равный 2R, для чего выберу на окружности (О; R) точку S и отложу три дуги, содержащие по 60º: SP=PQ=QT=60°. Точки S и T диаметрально противоположны.
3. Строю окружность (О; ST), пересекающую w1Что это за окружность? в точках М и N.
4. Теперь построю середину МО. Для этого строю окружности (O; OM) и (М; МО), а затем для точек М и О находим на них диаметрально противоположные точки U и V.
5. Далее строю окружность (U; UM), пересекающую (М; МО) в точках К и L.
6. Наконец, построю окружность (К; КМ) и (L; LM), пересекающиеся в искомой точке В – середине МО.
Треугольники КМВ и UMK равнобедренные и подобные. Поэтому из того, что КМ= 0,5МU, следует, что МВ=0,5МК=0,5R. Итак, точка В – искомая точка касания. Аналогично можно найти точку касания С.
Построения касательной к окружности, основанные на свойствах секущих, биссектрис.
1. Построю прямую ОА, она пересечен данную окружность в точках Р и Q.
2. Построю на отрезке АQ как на диаметре окружность.
3. Пересеку построенную окружность касательной l, проведенной через точку Р к окружности (О; r), и получу точки М и N.
4. Проведу МО и NО, они пересекут окружность (О; r) в точках В и С соответственно.
5. АВ и АС — искомые касательные.
По свойству секущей АМ²=АР·АQ. Поэтому окружность (А;АМ) пересечет окружность (О;R) в точках В и С касания искомых касательных АВ и АС.
Построение № 8
1. Построю окружность (А;АР), пресекающую прямую АР в точке D.
2. Построю окружность w на диаметре QD
3. Пересеку ее перпендикуляром к прямой АР в точке А и получу точки М и N.
Очевидно, что АМ²=АN²=АD·AQ=AP·AQ. Тогда окружность (А;АМ) пересекает (О;R) в точках касания В и С. АВ и АС — искомые касательные.
Видео:Построение прямой, параллельной даннойСкачать
673 К данной окружности постройте касательную, проходящую через данную точку вне окружности.
Решебник по геометрии за 8 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №673
к главе «Глава VIII. Окружность. §2. Центральные и вписанные углы».
Выделите её мышкой и нажмите CTRL + ENTER
Большое спасибо всем, кто помогает делать сайт лучше! =)
Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.
🎥 Видео
Окружность данного радиуса, проходящей через две заданные точкиСкачать
Построение касательной к окружностиСкачать
Построение касательной к окружностиСкачать
Касательные к окружностиСкачать
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать
Окружность. 7 класс.Скачать
Как с помощью одной линейки построить касательную к окружности?Скачать
Математика без Ху!ни. Уравнение касательной.Скачать
Построение касательной к окружностиСкачать
Как при помощи только линейки построить касательную к окружности?Скачать
№648. Постройте касательную к окружности с центром О: а) параллельную данной прямой;Скачать
Построение касательных к эллипсу. Изображение конусаСкачать
Построение касательных | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать
8 класс, 32 урок, Касательная к окружностиСкачать
Построение касательнойСкачать
