Условие принадлежности четырех точек одной окружности

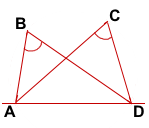
Признак принадлежности четырёх точек одной окружности

Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.

Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,

Доказать: точки A, B, C, D лежат на одной окружности

Обозначим ∠ABD=∠ACD=α.

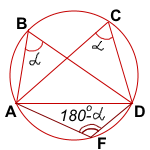
Опишем около треугольника ABD окружность.

Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.

Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:

Рассмотрим четырехугольник ACDF.

Отсюда следует, что четырёхугольник ABDF — вписанный.

Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.

Видео:ОГЭ Задание 25 Условие принадлежности четырёх точек одной окружностиСкачать

Презентация на тему «Признак принадлежности четырёх точек одной окружности»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Первое условие принадлежности четырех точек одной окружностиСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Описанная и вписанная окружности четырёхугольника Автор: учитель математики Румянцева Р.Г.

Признак принадлежности четырёх точек окружности

Признак принадлежности четырёх точек окружности Если точки А, М, N, В таковы что угол АМВ равен углу АNВ, причём точки M и N лежат в одной полуплоскости относительно прямой АВ, то точки А, М, N, В лежат на одной окружности.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 940 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 318 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 695 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 479 504 материала в базе

Материал подходит для УМК

«Геометрия», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.

§ 10. Описанная и вписанная окружности четырёхугольника

Видео:Условие принадлежности четырёх точек одной окружностиСкачать

Дистанционные курсы для педагогов

Другие материалы

• 25.11.2020
• 54

• 24.11.2020
• 138

• 24.11.2020
• 160

• 24.11.2020
• 158

• 24.11.2020
• 142

• 24.11.2020
• 270

• 24.11.2020
• 156

• 24.11.2020
• 88

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 25.11.2020 1023 —> —> —> —>
• PPTX 79.6 кбайт —> —>
• Оцените материал:

Настоящий материал опубликован пользователем Румянцева Рита Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На проекте: 5 лет и 1 месяц
• Подписчики: 0
• Всего просмотров: 2929
• Всего материалов: 7

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Первое условие принадлежности четырех точек окружностиСкачать

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Порядка 65% выпускников российских вузов идут работать по специальности

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Пандемия позволила детям получить больше внимания со стороны родителей

Время чтения: 1 минута

Переводить ЕГЭ по математике, физике и химии в компьютерный формат пока не планируется

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Принадлежность четырех точек одной окружности. Попытка 2.Скачать

ПРИНАДЛЕЖНОСТЬ ЧЕТЫРЕХ ТОЧЕК ОКРУЖНОСТИ В ОЛИМПИАДНЫХ ЗАДАЧАХ ПО ГЕОМЕТРИИ Текст научной статьи по специальности « Математика»

Видео:ОКРУЖНОСТЬ (признак принадлежности четырех точек одной окружности) ЧАСТЬ 4Скачать

Аннотация научной статьи по математике, автор научной работы — Морщинкина Юлия Дмитриевна, Сорокина Марина Валерьевна

Рассматривается вопрос необходимости и достаточности условий принадлежности четырех точек окружности . Приведены примеры заданий олимпиадного характера, в которых применяются различные критерии, такие как равноудаленность точек от центра, критерий вписанного четырехугольника , теорема, обратная равенству углов, опирающихся на одну хорду , свойства хорд , секущих и др.

Видео:ЕГЭ Задание 16 Условие принадлежности четырех точек окружностиСкачать

Похожие темы научных работ по математике , автор научной работы — Морщинкина Юлия Дмитриевна, Сорокина Марина Валерьевна

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Текст научной работы на тему «ПРИНАДЛЕЖНОСТЬ ЧЕТЫРЕХ ТОЧЕК ОКРУЖНОСТИ В ОЛИМПИАДНЫХ ЗАДАЧАХ ПО ГЕОМЕТРИИ»

ПРИНАДЛЕЖНОСТЬ ЧЕТЫРЕХ ТОЧЕК ОКРУЖНОСТИ В ОЛИМПИАДНЫХ ЗАДАЧАХ ПО ГЕОМЕТРИИ

Ю. Д. Морщинкина1, М. В. Сорокина2

1’2Пензенский государственный университет, Пенза, Россия

1 juliamorwinkina@mail.ru 2 sorokina_m@list.ru

Аннотация. Рассматривается вопрос необходимости и достаточности условий принадлежности четырех точек окружности. Приведены примеры заданий олимпиадного характера, в которых применяются различные критерии, такие как равноудаленность точек от центра, критерий вписанного четырехугольника, теорема, обратная равенству углов, опирающихся на одну хорду, свойства хорд, секущих и др.

Ключевые слова: олимпиадная задача по геометрии, окружность, вписанный угол, вписанный четырехугольник, хорда, секущая

Для цитирования: Морщинкина Ю. Д., Сорокина М. В. Принадлежность четырех точек окружности в олимпиадных задачах по геометрии // Вестник Пензенского государственного университета. 2021. № 4. С. 55-62.

В последние годы в образовательном процессе уделяется все больше внимания работе с одаренными детьми. Олимпиады различного уровня прочно вошли в школьную жизнь, и предметная подготовка обучающихся должна постоянно совершенствоваться. Дети, имеющие способности и интерес к предмету, с большим желанием включаются в работу олимпиадного движения. Однако, в такой предметной области, как математика, продвижение по пути решения нестандартных задач сопряжено с огромной работой. В учебном процессе учителем должна быть продумана система подготовки таких детей, разработаны программы, формирующие целостную систему математического знания, а также некоторые универсальные приемы работы с нестандартными задачами. Олим-пиадные задачи по геометрии характеризуются, конечно, нестандартностью подхода к решению. Это проявляется в нескольких аспектах: умение переформулировать требование задачи; умение грамотно выполнить чертеж, умение анализировать задачную ситуацию и искать путь решения и др. Олимпиадная задача по геометрии — это, как правило, задача на доказательство. Поэтому необходимо умение строить логическую цепочку умозаключений. Многие участники олимпиад, успешно справляющиеся с заданиями логического и алгебраического характера, испытывают трудности при решении задач по геометрии. В работе мы хотим остановиться на вопросе решения задачи на доказательство принадлежности четырех (или более) точек окружности. Задания подобного рода часто встречаются и во Всероссийской олимпиаде школьников по математике, и в уров-невых олимпиадах.

В школьном курсе геометрии окружность изучается достаточно подробно: дается определение, рассматриваются свойства углов, вписанных в окружность, теоремы, относящиеся к свойствам касательных, секущих, хорд [1]. Доказываются теоремы о треугольниках и четырехугольниках, вписанных в окружность. Поэтому в большинстве своем

© Морщинкина Ю. Д., Сорокина М. В., 2021

задачи, касающиеся принадлежности четырех точек окружности, у учащихся ассоциируются с четырехугольником, вписанным в окружность. При подготовке к олимпиадам необходимо рассмотреть вопрос равносильных преобразований этого требования, чтобы обучающиеся могли свободно оперировать фактами, выбирая тот, который будет наиболее удобным в каждом конкретном случае. Рассмотрим некоторые возможные варианты доказательства принадлежности четырех точек окружности.

1. Равноудаленность четырех точек от некоторой точки плоскости.

Это требование непосредственно вытекает из определения окружности, как геометрического места точек, равноудаленных от данной. И если в задаче возможно отыскание точки, равноудаленной от трех данных точек, то доказательство может быть проведено на основе именно равноудаленности, т.е. нужно рассматривать равенство четырех отрезков (радиусов окружности). Приведем пример задания, решение которого можно рассматривать с учащимися 8-9 классов.

Задача 1. На плоскости даны две пересекающиеся окружности. Точка А — одна из двух точек пересечения. В каждой окружности проведен диаметр, параллельный касательной в точке А к другой окружности, причем эти диаметры не пересекаются (рис. 1). Докажите, что концы этих диаметров лежат на одной окружности [2, № 108640].

Обозначим ш1 — окружность с центром в точке О и Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

HC AH HA CH AS CT

Из (9) и (10) следует: -=-. Значит, прямые АС и ST параллельны.

Четырехугольник HSKT — параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам. Если ST о HK = D, то D — середина отрезка ST, HD — медиана треугольника HST.

Так ST\AC, то лАНС -aSHT, следовательно, прямая НК, пересекающая сторону ST в ее середине, проходит через середину стороны АС. Значит, прямая HK содержит точку M.

Мы показали, что точка K, лежащая на окружности ю, принадлежит биссектрисе угла B и отрезку HM, следовательно, она совпадает с точкой R, поэтому R ею, что и требовалось доказать.

Мы рассмотрели несколько способов доказательства принадлежности точек окружности. Следует отметить, что существуют и другие варианты, например, использование симметрий или доказательство того, что четыре точки образуют четырехугольник специального вида. Примеры приведенных заданий позволят развить геометрический кругозор учащихся и будут полезны при подготовке к олимпиадам.

1. Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. [и др.]. Геометрия. 7-9 классы : учеб. для обще-образоват. организаций. 3-е изд. М. : Просвещение , 2015. 383 с.

2. Интернет-проект «Задачи». URL: http:// www.problems.ru. (дата обращения: 02.04.2021).

Информация об авторах Морщинкина Юлия Дмитриевна, студентка, Пензенский государственный университет.

Сорокина Марина Валерьевна, кандидат физико-математических наук, доцент, доцент кафедры «Математическое образование», Пензенский государственный университет.

Авторы заявляют об отсутствии конфликта интересов.

📸 Видео

ОГЭ 2021 Задание 24Скачать

10 класс, 11 урок, Числовая окружностьСкачать

Определение принадлежности точки окружностиСкачать

Второе условие принадлежности четырех точек окружностиСкачать

Точки на числовой окружностиСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

ОГЭ Задание 25 Две окружностиСкачать

ЕГЭ задание 16Скачать

Доказать, что точки лежат в одной плоскости - bezbotvyСкачать

Как проверить лежат ли 4 точки в одной плоскости Аналитическая геометрияСкачать

Окружность Эйлера (окружность 9 точек) и прямая ЭйлераСкачать

Доказать, что точки лежат на одной окружностиСкачать