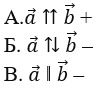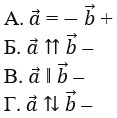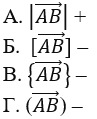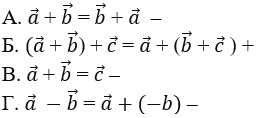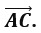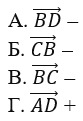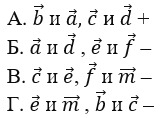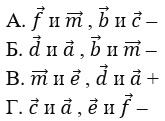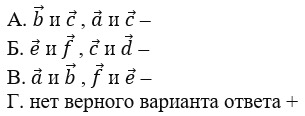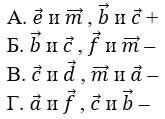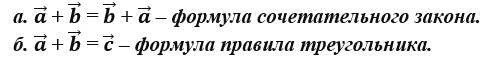Понятие вектора отрезок для которого указано

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Определение вектора

рис. 1

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Обозначение вектора

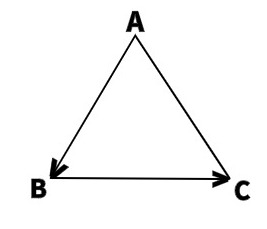
Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .

Видео:8 класс, 40 урок, Понятие вектораСкачать

Длина вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Видео:Понятие вектора. Видеоурок 1. Геометрия 9 классСкачать

Нулевой вектор

Нулевой вектор обычно обозначается как 0 .

Длина нулевого вектора равна нулю.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

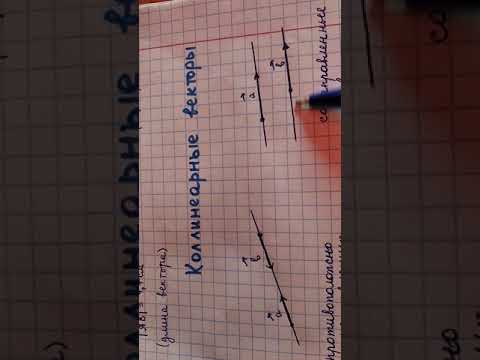
Коллинеарные вектора

рис. 2

Видео:Понятие вектора. Равенство векторов. Откладывание вектора от данной точкиСкачать

Сонаправленные вектора

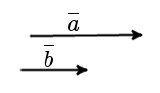рис. 3

Видео:10 класс, 38 урок, Понятие вектораСкачать

Противоположно направленные вектора

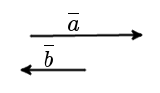рис. 4

Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Компланарные вектора

рис. 5

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Видео:Понятие вектора в пространстве. Видеоурок 16. Геометрия 10 классСкачать

Равные вектора

рис. 6

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

Видео:Полный разбор задач с векторами №2 ЕГЭ ПРОФИЛЬ 2024 | Профильная математика ЕГЭ 2024 | УМСКУЛСкачать

Единичный вектор

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Понятие вектора отрезок для которого указано

Тесты по геометрии 9 класс. Тема: «Векторы»

Правильный вариант ответа отмечен знаком +

1. Отрезок, для которого указано, какой из его концов является началом, а какой – концом, называется:

Г. нет верного варианта ответа –

2. Любая точка пространства может рассматриваться как вектор. Такой вектор называется:

3. Два ненулевых вектора, лежащие на одной прямой или на параллельных прямых, называются:

В. противоположно направленными –

4. Какие слова пропущены в предложении?

Если два ненулевых вектора коллинеарны, то они могут быть направлены либо одинаково (тогда их называют …), либо противоположно (тогда их называют …).

А. сонаправленные; разнонаправленные –

Б. противоположно направленные: сонаправленные –

В. сонаправленные: противоположно направленные +

Г. нет верного варианта ответа –

5. Длиной ненулевого вектора 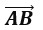называется:

Б. длина отрезка AB +

Г. нет верного варианта ответа –

6. Выберите верное обозначение сонаправленных векторов.

Г. нет верного варианта ответа –

7. Векторы называются равными, если:

А. они коллинеарны –

Б. их длины равны –

В. они сонаправлены –

Г. они сонаправлены и их длины равны +

8. Выберите верное обозначение противоположных векторов.

9. Выберите верное обозначение длины вектора

тест 10.

11. – это формула:

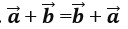
А. разности вектора –

Б. сочетательного закона –

В. нет верного варианта ответа –

Г. переместительного закона +

12. Выберите верную формулу сочетательного закона.

13. Вектор отложен от точки M. Точка M является:

А. концом вектора –

Б. началом вектора +

В. серединой вектора –

Г. нет верного варианта ответа –

14. Если длины двух ненулевых векторов равны, и они противоположно направлены, то они называются:

15. ABC – прямоугольный треугольник, 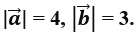Найдите длину вектора

16.

17. Найдите длину вектора

18. Дан правильный треугольник ABC со стороной 2. Найдите длину вектора

Г. недостаточно данных –

19. Выберите пары противоположно направленных векторов.

тест-20. Выберите пары сонаправленных векторов.

21. Выберите пары противоположных векторов.

22. Выберите пары равных векторов.

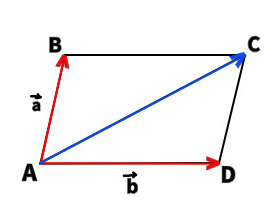
23. Дан параллелограмм ABCD, AC – диагональ Найдите сумму векторов

Г. нет верного варианта ответа –

24. Выберите верную формулировку правила многоугольника.

А. Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов. +

Б. От любой точки можно отложить вектор, равный данному, и притом только один. –

В. Чтоб сложить два вектора, нужно из произвольной точки отложить один вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало одного с концом второго. –

Г. Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов. –

25. Верны ли следующие суждения?

а. Векторы называются равными, если они коллинеарные и их длины равны.

б. Длиной нулевого вектора 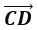является длина отрезка CD.

А. верно только а –

Б. верно только б +

В. оба суждения верны –

Г. оба суждения неверны –

26. Верны ли следующие суждения?

а. Направленный отрезок (вектор), длина которого равна нулю, – это нулевой вектор.

б. От любой точки можно отложить вектор, равным данному, и притом только один.

А. верно только а –

Б. верно только б –

В. оба суждения верны +

Г. оба суждения неверны –

27. Верны ли следующие суждения?

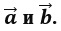
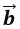
а. Разностью векторов называется такой вектор, сумма которого с вектором равна вектору

б. Два ненулевых вектора называются коллинеарными, если их длины равны и они противоположно направлены.

А. верно только а +

Б. верно только б –

В. оба суждения верны –

Г. оба суждения неверны –

28. Верны ли следующие суждения?

А. верно только а –

Б. верно только б +

В. оба суждения верны –

Г. оба суждения неверны –

29. Верны ли следующие суждения?

а. Вектор называется нулевым, если его начальная и конечная точка совпадает.

б. Модулем вектора называется длина вектора, выраженная числовым выражением.

А. верно только а –

Б. верно только б –

В. оба суждения верны +

Г. оба суждения неверны –

тест_30. Верны ли следующие суждения?

а. Скалярные величины характеризуются числом и направлением, а векторные только числом.

б. К векторным величинам относятся скорость, ускорение, перемещение.

Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Вектор. Виды векторов.

Вектор — в самом элементарном случае это математический объект, который характеризуется

величиной и направлением.

В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая

из его граничных точек является началом, а какая — концом.

У вектора есть длина и определенное направление. Графически вектора изображаются как

направленные отрезки прямой конкретной длины. Длина вектора – это и есть длина этого отрезка.

Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.

Как видно на рисунке, начало отрезка – это точка А, концом отрезка является

точка В, а непосредственно вектор обозначен через . У направления

вектора существенное значение, если переместить стрелку на другую

сторону отрезка, то получим вектор, но абсолютно другой. Понятие вектора

удобно сравнивать с движением физического тела: подумайте, ехать на

рыбалку и с рыбалки – разница огромная.

Понятия «больше» и «меньше» для векторов не имеет значения — так как направления их могут быть

разными. Сравнивают лишь длины векторов. Зато есть понятие равенства для векторов.

Виды векторов.

Единичным называется вектор, длина которого равна 1.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором.

У такого вектора конец и начало совпадают.

Нулевой вектор обычно обозначается как . Длина нулевого вектора, или его модуль равен нулю.

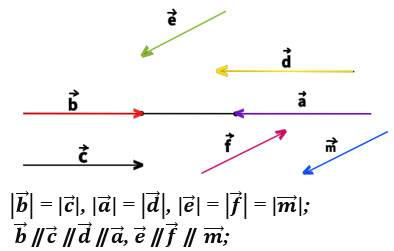
Коллинеарные вектора – вектора, которые параллельны одной прямой

или которые лежат на одной прямой.

Сонаправленные вектора. Два коллинеарных вектора a и b называются

сонаправленными векторами только тогда, когда их направления

соответствуют друг другу: a↑↑b

Противоположно направленные вектора – два коллинеарных вектора

a и b называются противоположно направленными векторами, только

когда они направлены в разные стороны: a↑↓b.

Компланарные вектора – это те вектора, которые параллельны одной

плоскости или те, которые лежат на общей плоскости.

В любое мгновение существует плоскость одновременно параллельную

двум любым векторам, поэтому два произвольных вектора являются

Равные вектора. Вектора a и b будут равными, если они будут лежать на

одной либо параллельных прямых и их направления и длины одинаковые.

То есть, такой вектор можно перенести параллельно ему в каждое место

Таким образом, два вектора равны, если они коллинеарные, сонаправленые

и имеют одинаковые длины:

Для координатного представления векторов огромное значение

оказывает понятие проекции вектора на ось (направленную

прямую).

Проекция вектора — это длина отрезка, который образуется

проекциями точек начала и конца вектора на заданную прямую,

при этом проекции добавляется знак “+”, но когда направление

проекции соответственно направлению оси, иначе — знак “–”.

Проекция – это длина заданного вектора, умноженная на cos угла исходного вектора и оси; проекция

вектора на ось, которая перпендикулярна ему = 0.

Когда работают с векторами, зачастую вводят так называемую

декартову систему координат и уже в этой системе находят

координаты вектора по базисным векторам.

Разложение по базису геометрически можно показать проекцией

вектора на координатные оси. Когда известны координаты начала и

конца вектора, то координаты данного вектора получают вычитая

из координат конца вектора координат начала вектора.

За базис зачастую выбираются координатные орты, которые обозначаются как , соответственно

осям x, y, z. Исходя из этого, вектор можно записать в таком виде:

Каждое геометрическое свойство есть возможность записать в координатах, и далее исследование

из геометрического переходит в алгебраическое и на этом этапе в основном упрощается. Обратное,

кстати, неверно: не у любого соотношения в координатах есть геометрическое толкование, но только

те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).

🎬 Видео

Понятие вектора | Геометрия 7-9 класс #76 | ИнфоурокСкачать

Координаты вектора в пространстве. 11 класс.Скачать

Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Понятие вектора. Коллинеарные векторы.Скачать

Скалярное произведение векторов. 9 класс.Скачать

Понятие вектора. Равенство векторов. Урок 1. Геометрия 9 классСкачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать