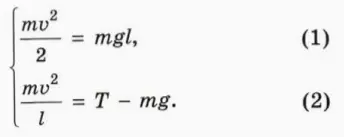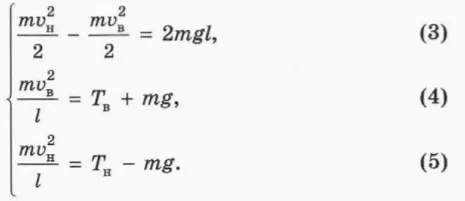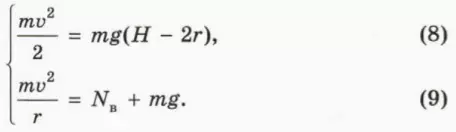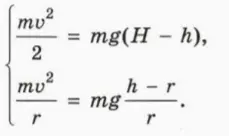- Тестирование онлайн
- Угловая скорость
- Период и частота
- Линейная скорость
- Центростремительное ускорение
- Вращение Земли
- Связь со вторым законом Ньютона
- Как вывести формулу центростремительного ускорения
- Движение по циклоиде*
- Неравномерное движение по окружности в вертикальной плоскости
- 1. Груз, подвешенный на нити и стержне
- «Шестикратный вес»
- В какой точке шарик сойдет с окружности?
- Груз, подвешенный на стержне
- 2. Движение по «мертвой петле»
- З. Соскальзывание с полусферы
- Дополнительные вопросы и задания
- Задача 1: минимальная скорость, необходимая для полного оборота шара
- 📹 Видео
Видео:Физика - движение по окружностиСкачать

Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Видео:Неравномерное движение по окружности в вертикальной плоскости (10 класс)Скачать

Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Видео:Неравномерное движение по окружности в вертикальной плоскостиСкачать
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Видео:Урок 90. Движение по окружности (ч.2)Скачать

Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Видео:Физика | Равномерное движение по окружностиСкачать

Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть 

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью 
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Видео:Вращение камня в верт. плоскостиСкачать

Неравномерное движение по окружности в вертикальной плоскости
1. Груз, подвешенный на нити и стержне
Шарик массой m подвешен в точке O на нити длиной l (рис. 33.1). Отведем его на угол 90′ и отпустим без толчка. Шарик начнет двигаться по окружности.
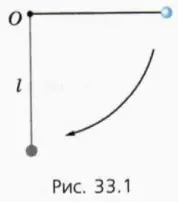
Обозначим 
? 1. Используя рисунок 33.2, ответьте на вопросы:
а) Какие силы показаны на рисунке?
б) Как направлено ускорение шарика?
в) Выразите модуль равнодействующей через модули показанных сил.
? 2. Перенесите в тетрадь рисунок 33.2, укажите на нем ускорение шарика и объясните смысл следующих уравнений:
? 3. Шарик массой 100 г подвешен на нити длиной 1 м. Его отклоняют на 90º и отпускают без толчка.
а) Чему равна сила натяжения нити, когда шарик проходит положение равновесия?
б) Во сколько раз вес шарика при прохождении положения равновесия больше силы тяжести?
Подсказка. Чтобы найти силу натяжения нити, удобно разделить уравнение (2) иа уравнение (1). Вспомните определение веса тела.
Итак, в данном случае при прохождении шариком положения равновесия нить должна выдержать «тройной вес»!
Сообщим шарику в нижней точке такую скорость 
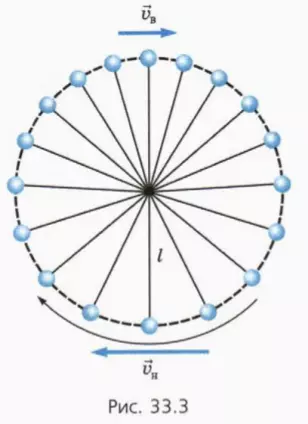
На рисунке показаны последовательные положения шарика через равные промежутки времени (их можно зафиксировать, например, с помощью видеосъемки).
? 4. Почему в верхней части рисунка расстояния между последовательными положениями шарика меньше?
? 5. Сделайте в тетради чертеж, на котором изобразите:
а) силы, действующие на шарик в верхней и нижней точках окружности (обозначьте 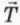
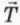
б) ускорение шарика в этих точках. В верхней точке ускорение направлено вниз, а в нижней – вверх.
? 6. Объясните смысл следующих уравнений:
? 7. Подвешенный на нити шарик массой 100 г вращается в вертикальной плоскости. Насколько больше сила натяжения нити, когда шарик проходит положение равновесия, чем когда он находится в верхней точке окружности?
Подсказка. Удобно вычесть уравнение (4) из уравнения (б) и сравнить полученное уравнение с уравнением (3).
«Шестикратный вес»
Шарик движется но окружности при условии, что нить натянута. Поэтому минимальная скорость, которую нужно сообщить шарику в нижней точке, чтобы он стал двигаться по окружности„должна быть такой, чтобы сила натяжения нити обратилась в нуль только в верхней точке окружности.
? 8. Шарику, подвешенному на нити длиной l, сообщили в нижней точке минимальную горизонтальную скорость, необходимую для того, чтобы он начал двигаться по окружности. Сделайте чертеж, на котором изобразите силы, действующие на шарик в верхней и нижней точках окружности. Чему в этом случае равны:
а) скорость шарика в верхней точке окружности?
б) ускорение шарика в верхней точке окружности?
в) скорость шарика в нижней точке окружности?
г) вес шарика в нижней точке окружности?
Подсказка. Воспользуйтесь уравнениями (3)–(5).
Итак, когда груз проходит нижнюю точку, нить должна выдерживать шестикратный вес груза!
В какой точке шарик сойдет с окружности?
Пусть теперь скорость шарика в нижней точке недостаточна для того, чтобы он мог совершить полный оборот.
В таком случае есть две возможности.
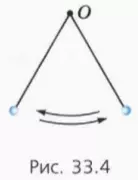
1) Шарик не поднимется выше точки подвеса О. Тогда он начнет колебаться между крайними положениями (рис. 33.4).
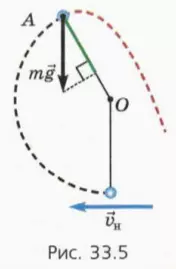
2) Шарик поднимется выше точки подвеса, но сила натяжения нити обратится в некоторой точке А в нуль (рис. 33.5). После этого шарик будет двигаться по параболе, показанной красным пунктиром. Когда шарик находится в точке А, центростремительное ускорение ему сообщает только составляющая силы тяжести, направленная вдоль радиуса к центру окружности. На рисунке показано, как найти модуль этой составляющей (отрезок зеленого цвета).
? 9. Шарику массой m, подвешенному на нити длиной l, сообщают горизонтальную начальную скорость v0. Когда шарик находится на высоте h, сила натяжения нити обращается в нуль. Обозначим скорость шарика в этот момент. Используя рисунок 33.6:
а) объясните смысл уравнений
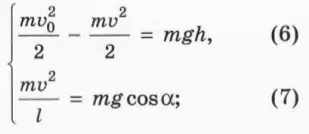
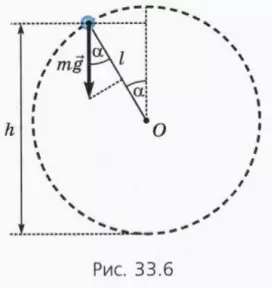
б) выразите h через l и альфа.
? 10. Шарику массой 200 г, подвешенному на нити длиной 50 см, сообщают горизонтальную скорость 4 м/с.
а) До какой высоты (по отношению к положению равновесия) шарик будет двигаться по окружности?
б) Чему будет равна сила натяжения нити, когда шарик будет находиться на одной горизонтали с точкой подвеса?
Подсказка. Когда шарик находится на одной горизонтали с точкой подвеса, центростремительное ускорение шарику сообщает только сила натяжения нити.
? 11. Небольшая шайба массой m лежит внутри закрепленного цилиндра. Ось цилиндра горизонтальна (рис. 33.7). Внутренний радиус цилиндра 30 см, стенки цилиндра гладкие. Какую скорость v0 надо сообщить шайбе перпендикулярно оси цилиндра, чтобы она:
а) совершила полный оборот, двигаясь по окружности?
б) оторвалась от поверхности цилиндра на высоте 40 см?
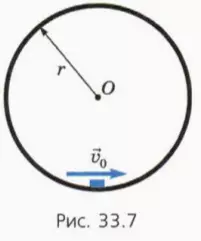
Подсказки. Движение шайбы в цилиндре отличается от движения подвешенного на нити шарика только тем, что роль силы натяжения нити играет сила нормальной реакции, а длину нити l надо заменить на радиус цилиндра r.
Груз, подвешенный на стержне
Рассмотрим теперь вращение груза, подвешенного на легком стержне (массой стержня можно пренебречь). В отличие от нити стержень сохраняет форму и поэтому не дает грузу сойти с окружности. По этой причине минимально возможная скорость груза в верхней точке равна нулю.
? 12. Шарик подвешен на легком стержне длиной l, который может вращаться без трения вокруг точки подвеса O.
а) Какова минимально возможная скорость шарика в верхней точке траектории?
б) Какую минимальную скорость надо сообщить шарику в нижней точке, чтобы он совершил полный оборот?
в) Чему равен вес шарика в нижней точке?
Итак, подвешенному на стержне шарику надо сообщить меньшую начальную скорость, чтобы он сделал полный оборот, чем в случае, когда шарик подвешен на нити той же длины.
2. Движение по «мертвой петле»
Рассмотрим движение тела в вертикальной плоскости по гладкому желобу, переходящему в окружность (рис. 33.8). По аналогии с фигурой высшего пилотажа, когда самолет совершает круговой виток в вертикальной плоскости, такое движение называют иногда мертвой петлей.
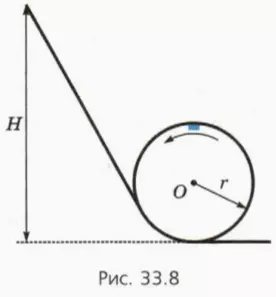
Движение по круговому желобу очень похоже на рассмотренное выше движение подвешенного на нити груза. Роль действующей на груз силы натяжения нити 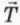

? 13. Небольшая шайба массой m соскальзывает с высоты H по гладкому наклонному желобу, переходящему в окружность радиусом r, и движется по окружности, не отрываясь от желоба. Обозначим 
а) Сделайте чертеж, на котором изобразите силы, действующие на шайбу в верхней и нижней точках окружности.
б) Объясните смысл следующих уравнений:
? 14. Чему равна минимальная высота Hmin, с которой должна соскальзывать шайба, чтобы она могла совершить полный оборот?
Подсказка. В этом случае Nв обращается в нуль в верхней точке окружности.
Если начальная высота шайбы H меньше, чем Hmin, то в некоторой точке шайба оторвется от желоба. В этой точке сила нормальной реакции обращается в нуль.
? 15. Небольшая шайба массой m соскальзывает с высоты H по гладкому желобу, переходящему в окружность радиусом r, и отрывается от желоба на высоте h (по отношению к нижней точке окружности). Скорость шайбы в этот момент обозначим v.
а) Сделайте чертеж, на котором изобразите силы, действующие на шайбу в момент отрыва от желоба.
б) Используя этот чертеж, объясните смысл уравнений
? 16. Небольшая шайба массой 50 г соскальзывает с некоторой высоты H по гладкому желобу, переходящему в окружность радиусом 30 см, и отрывается от желоба на высоте 40 см (по отношению к нижней точке окружности).
а) Чему равно H?
б) С какой силой шайба давит на желоб, когда она находится на одной горизонтали с центром окружности?
З. Соскальзывание с полусферы
Пусть на вершине гладкой полусферы радиусом г, укрепленной на столе, лежит небольшая шайба массой m (рис. ЗЗ.9). От незначительного толчка шайба начинает соскальзывать.

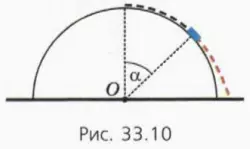
Пока шайба скользит, действующая на нее сила нормальной реакции уменьшается. В некоторой точке она обратится в нуль – в этот момент шайба оторвется от полусферы (рис. 33.10) и начнет двигаться по параболе (красная пунктирная линия). Обозначим и скорость шайбы в момент отрыва от полусферы.
? 17. Сделайте чертеж, на котором изобразите силы, действующие на шайбу в момент отрыва от полусферы, и направление скорости шайбы в этот момент. Обозначьте h высоту, на которой находится при этом шайба, а α – угол между радиусом, проведенный к шайбе и вертикалью. Используя этот чертеж:
а) объясните смысл уравнений

б) выразите h через r и α.
в) выразите h через r.
? 18. На вершине гладкой сферы лежит небольшая шайба массой m, соединенная нитью с грузом массой M (рис. 33.11). В начальный момент тела покоятся. Их отпускают без толчка. Шайба отрывается от полусферы, когда угол между радиусом, проведенным к шайбе, и вертикалью равен α. Обозначим и модуль скорости тел в момент отрыва.

а) Сделайте чертеж, на котором изобразите силы, действующие на шайбу в момент отрыва от полусферы.
Подсказка. В момент отрыва на шайбу действуют только сила тяжести и сила натяжения нити, направленная по касательной к окружности.
б) Насколько опустилась шайба и насколько опустился груз к моменту отрыва шайбы по сравнению с их начальным положением?
Подсказка. См. рисунок 33.12. Шайба опустилась на расстояние, отмеченное синим отрезком, а груз опустился на расстояние (зеленый отрезок), равное длине дуги, пройденной шайбой до отрыва (зеленый пунктир). Длина дуги равна rα (где α задано в радианах).
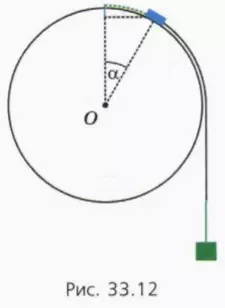
в) Используя этот чертеж, объясните смысл уравнений
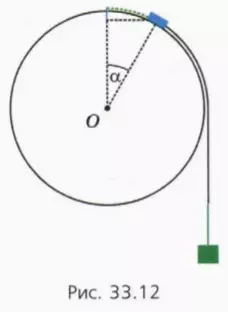
Подсказка. Действующая на шайбу сила натяжения нити направлена по касательной к окружности. Поэтому центростремительное ускорение шайбе перед самым отрывом сообщает только составляющая действующей на шайбу силы тяжести, направленная по радиусу к центру окружности.
г) Чему равно отношение M/m, если α = π/6?
Дополнительные вопросы и задания
19. Какую скорость можно сообщить шарику в нижней точке, чтобы он начал совершать колебания, если:
а) шарик подвешен на нити длиной l?
б) шарик подвешен на легком стрежне длиной l?
Подсказка. Шарик на нити не должен подняться выше точки подвеса, а шарик на стержне не должен достичь верхней точки окружности.
20. Небольшая шайба массой m соскальзывает с высоты H = 2r по гладкому желобу, переходящему в окружность с радиусом r.
а) На какой высоте h (по отношению к нижней точке окружности) шайба оторвется от желоба?
б) С какой силой шайба давит на желоб, когда она находится на одной горизонтали с центром окружности?
21. На гладкой полусфере радиуса r, укрепленной на столе, лежит небольшая шайба. Ей сообщают начальную горизонтальную скорость v0. На какой высоте h от стола шайба оторвется от полусферы?
Подсказка. Если начальная скорость достаточно велика, шайба оторвется от полусферы сразу.
22. На укрепленной на столе полусфере радиуса r лежит небольшая шайба массой m. От незначительного толчка шайба начинает соскальзывать. Вследствие трения за время, в течение которого шайба скользила по полусфере, выделилось количество теплоты Q.
а) На какой высоте h шайба оторвалась от полусферы?
б) На какой высоте h шайба оторвалась от полусферы, если выделившееся количество теплоты равно кинетической энергии шайбы в момент отрыва?
23. Впервые в мире круговой виток в вертикальной плоскости выполнил русский летчик П. Н. Нестеров в 1913 году. Эту фигуру высшего пилотажа называют мертвой петлей или петлей Нестерова. Нестеров так доверял своим расчетам, что перед выполнением мертвой петли не пристегнулся ремнями к креслу пилота. Расчет летчика оказался правильным: ремни не понадобились! Почему при выполнении мертвой петли летчик не выпадает из кресла пилота в верхней точке траектории?
Видео:Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Задача 1: минимальная скорость, необходимая для полного оборота шара
Шар подвешен на невесомой нерастяжимой нити длиной l = 0,5 м. Какую минимальную горизонтально направленную скорость vo надо сообщить шару, чтобы он сделал полный оборот в вертикальной плоскости?
Эта задача была размещена посетителями в разделе Решаем вместе 25 мая 2007 года.
Воспользуемся законом сохранения механической энергии при переходе шарика из нижнего положения в верхнее:
| mvo 2 | = mg • 2l + | mv 2 | (1), |
| 2 | 2 |
где l — длина подвеса или нерастяжимой нити.
В верхней точке на шарик будут действовать 2 силы: сила тяжести mg (направлена вниз) и сила натяжения нити T (также направлена вниз). Эти силы сообщают шарику центростремительное ускорение, направленное вниз — к точке подвеса:
Поскольку шарик достиг верхней точки (T = 0, условие задачи), то
| mv 2 | = mg |
| l |
отсюда
Сделаем подстановку (2) в (1), получим
| mvo 2 | = 2mgl + | mgl |
| 2 | 2 |
vo 2 = g4l + gl = 5gl.
Выполнив вычисления, получим: vo = √(5×10×0,5) = 5 (м/с).
Ответ: если шарик подвешен на нерастяжимой нити, его скорость должна составлять не менее 5 м/с.
Примечание: если шар подвешен на жестком стержне, то в верхней точке скорость v может обратиться в нуль, тогда из (1)
| mvo 2 | = mg•2l, отсюда |
| 2 |
Произведя вычисления, получим: vo = 2×√(10×0,5) = 4,47 (м/с).
📹 Видео
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Линейная и угловая скорости при равномерном движении по окружностиСкачать

Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

РТ-2023 3-й этап B6 "Шар с пулей"Скачать

Центростремительное ускорение. 9 класс.Скачать

ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. Кирик 9 классСкачать

Движение по окружностиСкачать

9 класс, 24 урок, Движение тел по окружностиСкачать

Физика ЕГЭ | Динамика и кинематика вращательного движения | Движение по окружности | ЕГЭ на 100 !Скачать