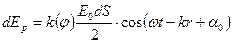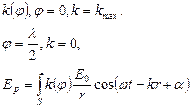Почему кольца ньютона имеют вид концентрических окружностей (6 видео)

Почему кольца ньютона имеют вид концентрических окружностей

Волна, отраженная от верхней поверхности линзы, в силу небольшой длины когерентности обычных источников света, некогерентна с волнами, отраженными от поверхностей зазора, и участия в образовании интерференционной картины не принимает. Поэтому мы ее и не будем учитывать.

При нормальном падении света кольца в отраженном свете имеют вид концентрических окружностей с центром в точке соприкосновения линзы с пластинкой. Найдем радиусы темных колец (минимумов).

Сначала запишем условие образования темных колец. Они возникают там, где оптическая разность хода волн, отраженных от обеих поверхностей зазора, равна нечетному числу полуволн:

где связано с «потерей» полуволны при отражении от пластинки и . Отсюда

Далее, согласно теореме Пифагора (см. рис. 13), . Учитывая, что , получим

Из (37) и (38) следует, что радиус -го темного кольца

Заметим, что значению соответствует минимум темного пятна (не кольца). Аналогичный расчет можно провести и для светлых колец. Пример . Найдем радиус 5-го светлого кольца, если радиус кривизны выпуклой поверхности линзы и контакт ее с плоской поверхностью стекла идеальный (в точке). Длина волны света . Условие максимумов в данном случае имеет вид

где — толщина зазора в месте — го максимума (заметим, что если бы мы взяли , то значения надо было начинать с нуля). Согласно (38), . Из этих двух соотношений следует, что искомый радиус

Следует обратить внимание на то, что формула (39) справедлива лишь в случае идеального (точечного) контакта сферической поверхности линзы с пластинкой. Но идеальных контактов не бывает, номера колец не равны, вообщя говоря, порядку интерференции , и это обстоятельство необходимо учитывать при расчетах (см. задачу 5 из раздела 1.4 «Примеры решения задач»). Если линзу постепенно отодвигать от поверхности пластинки, то интерференционные кольца будут стягиваться к центру: это ведь кольца (полосы) равной толщины, а она при этом перемещается к центру. С помощью колец Ньютона можно с достаточно высокой точностью контролировать качество изготовления, например, сферических поверхностей. Рассмотрим теперь на конкретном примере вопрос, связанный с причиной локализации колец Ньютона в очень малой области для обычных линз (кольца приходится рассматривать в микроскоп).

Пример . Плосковыпуклая линза, радиус кривизны сферической поверхности которой мм, соприкасается со стеклянной пластинкой. Оценим радиус наблюдаемой в отраженном свете интерференционной картины, если длина волны света и . Свет падает практически нормально. При нормальном падении света ограничивать интерференционную картину будет только длина когерентности . Кольца исчезают при условии , где — ширина зазора в месте исчезновения колец. Согласно (38), , а . Из этих формул получим , откуда

Число видимых колец равно . Этот результат можно получить и с помощью (39).

Содержание

Кольца Ньютона
Кольца Ньютона
Длина световой волны
Ход лучей в проходящем свете кольца ньютона
Содержание
Описание [ править | править код ]
Классическое объяснение явления [ править | править код ]
Использование [ править | править код ]
💡 Видео

Видео:Урок 417. Кольца НьютонаСкачать

Кольца Ньютона

Простая интерференционная картина возникает в тонкой прослойке воздуха между стеклянной пластиной и положенной на нее плоско-выпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны. Эта интерференционная картина имеет вид концентрических колец, получивших название кольца Ньютона.

Видео:Кольца Ньютона - интерференция в клиновидных пластинкахСкачать

Кольца Ньютона

Возьмите плоско-выпуклую линзу с малой кривизной сферической поверхности и положите ее на стеклянную пластину, как было указано выше. Внимательно разглядывая плоскую поверхность линзы (лучше через лупу), вы обнаружите в месте соприкосновения линзы и пластины темное пятно и вокруг него совокупность маленьких радужных колец. Расстояния между соседними кольцами быстро убывают с увеличением их радиуса. Это и есть кольца Ньютона. Ньютон наблюдал и исследовал их не только в белом свете, но и при освещении линзы одноцветным (монохроматическим) пучком. Оказалось, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному; красные кольца имеют максимальный радиус. Все это вы можете проверить с помощью самостоятельных наблюдений.

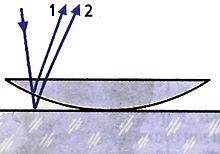
Но объяснить, почему возникают кольца Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда волна определенной длины падает почти перпендикулярно на плоско-выпуклую линзу. Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны: они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга. Вызываемые ими колебания происходят в одной фазе.

Напротив, если вторая волна отстанет от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.

Кольца Ньютона в отражённом свете

Длина световой волны

Длина световой волны. Для красного света измерения дают λ = 8∙10 -7 м, а для фиолетового — λ = 4∙10 -7 м. Длины волн, соответствующие другим цветам спектра, принимают промежуточные значения. Для любого цвета длина световой волны очень мала. Представьте себе среднюю морскую волну длиной в несколько метров, которая увеличилась настолько, что заняла весь Атлантический океан от берегов Америки до Европы. Длина световой волны в том же увеличении лишь ненамного превысила бы ширину этой страницы.

Явление интерференции не только доказывает наличие у света волновых свойств, но и позволяет измерить длину волны. Подобно тому, как высота звука определяется его частотой, цвет света определяется частотой колебаний или длиной волны.

Вне нас в природе нет никаких красок, есть лишь волны разной длины. Глаз — сложный физический прибор, способный обнаруживать различие в цвете, которому соответствует весьма незначительная (около 10 -6 см) разница в длине световых волн. Интересно, что большинство животных не способны различать цвета. Они всегда видят черно-белую картину.

При переходе света из одной среды в другую длина волны изменяется. Это можно обнаружить так. Заполним водой или другой прозрачной жидкостью с показателем преломления п воздушную прослойку между линзой и пластиной. Радиусы интерференционных колец уменьшатся.

Почему это происходит? Мы знаем, что при переходе света из вакуума в какую-нибудь среду скорость света уменьшается в п раз. Так как v=λv, то при этом должна уменьшиться в п раз либо частота, либо длина волны. Но радиусы колец зависят от длины волны. Следовательно, когда свет входит в среду, изменяется в п раз именно длина волны, а не частота.

Видео:кольца НьютонаСкачать

Ход лучей в проходящем свете кольца ньютона

Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину.

Ньютона кольца наблюдаются и в проходящем и – более отчётливо – в отражённом свете.

Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны, то есть они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга.

, где m – любое целое число, лямбда – длина волны.

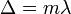
Напротив, если вторая волна отстает от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.

Для учета того, что в разных веществах скорость света различна, для определения положения min и max используют не разность хода, а оптическую разность хода. Разность оптических длин пути называется оптическая разность хода.

— оптическая длина пути, — оптическая разность хода.

Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Необходимо так же учитывать тот факт, что при отражении световой волны от оптически более плотной среды фаза волны меняется на Пи , этим объясняется тёмное пятно в точке соприкосновения линзы и плоскопараллельной пластины. Линии постоянной толщины воздушной прослойки под сферической линзой представляют собой концентрические окружности при нормальном падении света, при наклонном — эллипсы.

Радиус k-го светлого кольца Ньютона (в предположении постоянного радиуса кривизны линзы) в отражённом свете

выражается следующей формулой: где

R — радиус кривизны линзы; k = 2, 4, …; λ — длина волны света в вакууме;

n — показатель преломления среды между линзой и пластинкой.

Дата добавления: 2015-04-24 ; Просмотров: 26654 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Прихотливый вид интерференционных картин в тонких пленках объясняется, как сказано, случайными неравномерностями в толщине пленки. В пленке, имеющей вид клина, области одинаковой толщины вытянуты вдоль ребра клина и в соответствии с этим так же расположены темные и светлые (цветные) полосы интерференции.

Очень важным видоизменением опыта с клинообразной пленкой является опыт, произведенный еще в 1675 г. Английский физик и математик Исаак Ньютон (1643—1727) наблюдал цвета тонкой

Рис. 267 прослойки воздуха, заключенной между плоским стеклом и выпуклой поверхностью объектива астрономического рефрактора. Радиус кривизны выпуклой поверхности объектива в опыте Ньютона был около 10 м, поэтому толщина прослойки воздуха между плотно сжатыми стеклами очень медленно и правильно возрастала от места соприкосновения стекол (где она равна нулю) к наружным частям объектива.

Если смотреть на такую систему, то темное место соприкосновения обоих стекол оказывается окруженным светлой кольцевой полосой, которая постепенно переходит в темную, вновь сменяется светлой и т. д. По мере увеличения диаметра кольца толщина воздушной прослойки возрастает неравномерно, воздушный клин становится все круче и соответственно ширина кольцевых полос, т. е. расстояние между двумя соседними минимумами, становится меньше. Такова картина, наблюдаемая в монохроматическом свете; в белом свете наблюдается система цветных колец, постепенно переходящих друг в друга. По мере удаления от центрального темного пятна цветные полосы становятся все уже и белесоватое благодаря перекрытию цветов, пока, наконец, не исчезают всякие следы интерференционной картины.

На основании изложенного выше нетрудно понять, почему интерференционная картина имеет в данном случае вид системы концентрических колец. Места равной толщины в воздушной прослойке, которые соответствуют местам с одинаковой разностью хода световых волн, имеют форму окружностей. По этим окружностям и располагаются места равной интенсивности в интерференционной картине.

Удобное расположение приборов, позволяющее наблюдать и промерять кольца Ньютона, изображено на рис. 267. На столике микроскопа с небольшим увеличением расположено плоское стекло, сложенное с линзой малой кривизны. Наблюдение ведется через микроскоп по направлению, перпендикулярному к плоскости стекла. Для того чтобы освещающий свет также падал перпендикулярно к плоскости стекла, заставляют свет источника отражаться от стеклянной пластинки, поставленной под углом 45° к оси микроскопа. Таким образом, интерференционная картина рассматривается сквозь эту стеклянную пластинку. Практически пластинка не мешает наблюдению колец, ибо сквозь нее проходит вполне достаточно света. Для усиления освещения можно применять конденсор. Источником света служит горелка, пламя которой окрашено парами натрия (монохроматический свет), или лампочка накаливания, которую можно прикрывать цветными светофильтрами.

Для того чтобы использовать интерференционные явления, в частности кольца Ньютона для измерения длины волны, надо подробнее рассмотреть условия образования максимумов и минимумов света.

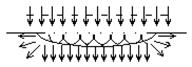
При падении света на пленку или тонкую пластинку часть света проходит сквозь нее, а часть отражается. Предположим, что монохроматический свет длины волны l падает на пластинку перпендикулярно к ее поверхности. Будем рассматривать малый участок пластинки, считая его плоскопараллельным. На рис. 268 изображен ход лучей в пластинке, причем для наглядности лучи изображены не вполне перпендикулярными к ней. В отраженном свете имеем луч 1, отраженный от верхней поверхности пластинки и луч 2, отраженный от нижней поверхности. В проходящем — луч 1′, прямо прошедший через пластинку и луч 2′, отразившийся по одному разу от нижней и от верхней поверхностей. Рассмотрим сначала проходящие лучи. Лучи 1′ и 2′ обладают разностью хода, так как первый прошел через нашу пленку один раз, а второй — три раза. Образовавшаяся разность хода при нормальном падении света есть AB+BC+CD—АВ=ВС+CD=2h, где h — толщина пластинки. Если эта разность хода равна целому числу волн, т. е. четному числу полуволн, то лучи усиливают друг друга; если же разность хода равна нечетному числу полуволн, то лучи взаимно ослабляются. Итак, максимумы и минимумы получаются в тех местах пластинки, толщина которых h удовлетворяет условию 2h=nλ/2, причем минимумы соответствуют нечетному значению n=1, 3, 5, . максимумы соответствуют четному значению n=2, 4, . Таковы выводы для проходящего света.

Рис. 268. Ход отраженных и проходящих лучей при двукратном отражении в пленке

В отраженном свете разность хода между лучами 1 и 2 при нормальном падении света есть AB+BC=2h, т. е. такая же, как и для проходящего света. Можно было бы думать, что и в отраженном свете максимумы и минимумы будут на тех же местах пластинки, что и в проходящем свете. Однако это означало бы, что места пластинки, которые меньше всего отражают света, меньше всего и пропускают его. В частности, если бы вся пластинка имела одну и ту же толщину и притом такую, что 2h равно нечетному числу полуволн, то такая пластинка давала бы и минимальное отражение, и минимальное пропускание. Но так как мы предполагаем, что пластинка не поглощает света, то одновременное ослабление и отраженного, и пропущенного света невозможно. Само собой разумеется, что в непоглощающей пластинке свет отраженный должен дополнять свет прошедший, так что темные места в проходящем свете соответствуют светлым в отраженном и наоборот. И действительно, опыт подтверждает это заключение.

В чем же ошибочность нашего расчета интерференции отраженных световых волн? Дело в том, что мы не учли различия в условиях отражения. Некоторые из отражений имеют место на границах воздух — стекло, а другие на границах стекло — воздух (если речь идет о тонкой стеклянной пластинке в воздухе). Это различие приводит к возникновению дополнительной разности фаз, которая соответствует дополнительной разности хода, равной λ/2. Поэтому полная разность хода для лучей, отраженных от верхней и нижней поверхностей пластинки толщиной h, равняется 2h+λ/2. Места минимумов соответствуют условию 2h+2λ/2 = mλ/2.

где m — нечетное число; места максимумов — четным значениям m. Следовательно, максимумы и минимумы получаются в тех местах пластанки, толщина которых h удовлетворяет условию 2h = (m-1)λ/2 = nλ/2, причем (m-1) обозначено через n. Минимумы соответствуют четным значениям n=0, 2, 4, . максимумы соответствуют нечетным значениям n=1, 3, 5, .

Сопоставим результаты, полученные для определения положения максимумов и минимумов в проходящем и отраженном свете. Положения максимумов и минимумов соответствуют толщине пленки, определяемой из условия: 2h=nλ/2.

Таким образом, области максимумов в проходящем свете соответствуют областям минимумов в отраженном и, наоборот.

Применительно к кольцам Ньютона, которые обычно наблюдаются в отраженном свете (§ 126), получаем, что места максимумов соответствуют нечетным значениям n=1, 3, 5, . а места минимумов — четным n=0, 2, 4, . Центральный (нулевой n=0) минимум имеет вид темного кружка, следующее первое темное кольцо соответствует

n=2, второе n=4 и т. д. Вообще номер N темного кольца связан с числом я соотношением N=n/2. Номер N светлого кольца выражается через n формулой N=(n+1)/2.

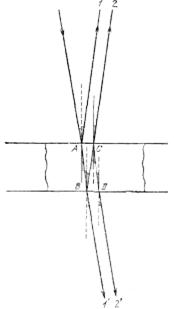
Вместо определения толщины h того места воздушной прослойки, которое соответствует кольцу номера N, удобнее измерять диаметр или радиус соответствующего кольца. Из рис. 269 следует: R2=(R—h)2+r 2 и, следовательно, толщина прослойки h связана с радиусом кольца r и радиусом линзы R соотношением (2R-h)h=r 2

Для опытов с кольцами Ньютона пользуются линзами о очень большим радиусом R (несколько метров). Поэтому можно пренебречь величиной ft по сравнению с 2R и упростить последнее соотношение, записав: 2Rh=r 2 или 2h=r 2 /R.

Итак, для определения длины волны l с помощью колец Ньютона имеем 2h=r 2 /R

Если измеряются радиусы темных колец, то номер кольца N=n/2. В таком случае длина волны выразится формулой

λ = r 2 _N /NR, где r_N есть радиус N-го темного кольца.

Рис. 269. К расчету радиусов колец Ньютона

Проводя измерения радиусов светлых колец, мы должны иметь в виду, что N=_N /(2N-1)R, где r_N есть радиус N-ro светлого кольца.

20. Дифракция света. Дифракция Фраунгофера и Френеля. Принцип Гюйгенса–Френеля.

Дифракция – совокупность явлений, наблюдаемых при распространении света вблизи границ прозрачных и непрозрачных тел сквозь малые отверстия и щели, через различные препятствия, связанных с отклонением от законов геометрической оптики. При дифракции происходит перераспределение светового потока в пространстве.

При интерференции наблюдается результат суперпозиции волн, возбужденных конечным числом дискретных когерентных источников.

При дифракции света наблюдается суперпозиция световых волн, возбуждаемых когерентными источниками, расположенных непрерывно.

Две схемы наблюдения дифракции:

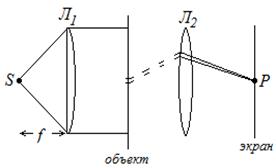
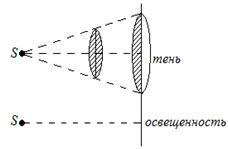
– дифракция Фраунгофера — это дифракция на отверстии, которое для точки наблюдения открывает заметно меньше одной зоны Френеля. Это условие выполнено, если точка наблюдения и источник света находятся достаточно далеко от отверстия.

дифракция Френеля — это дифракция в случае, когда отверстие открывает (или препятствие закрывает) для точки наблюдения несколько зон Френеля. Если открыто много зон Френеля, то дифракцией можно пренебречь, и мы оказываемся в приближении геометрической оптики.

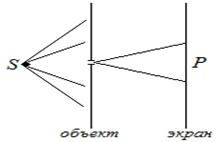
Принцип Гюйгенса (к XVIIв.) каждая точка, до которой доходит световая волна, служит центром вторичных волн, огибающая этих волн даёт положение волнового фронта по следующему моменту времени.

Френель для количественного решения задач о дифракции дополнил принцип Гюйгенса положением о интерференции вторичных волн.

Принцип Гюйгенса — Френеля формулируется следующим образом: Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

– амплитуда волны точечного источника,

– сигнал, излучающий повторяемость dS

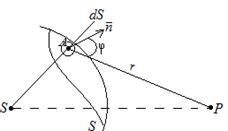
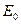
Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени.

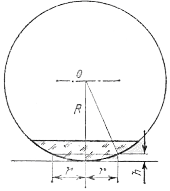
Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис. 256). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в однородной изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т. е. волна огибает края отверстия.

Явление дифракции характерно для волновых процессов. Поэтому если свет является волновым процессом, то для него должна наблюдаться дифракция, т. е. световая волна, падающая на границу какого-либо непрозрачного тела, должна огибать его (проникать в область геометрической тени). Из опыта, однако, известно, что предметы, освещаемые светом, идущим от точечного источника, дают резкую тень и, следовательно, лучи не отклоняются от их прямолинейного распространения. Почему же возникает резкая тень, если свет имеет волновую природу? К сожалению, теория Гюйгенса ответить на этот вопрос не могла.

Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а следовательно, и об интенсивности волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.

Согласно принципу Гюйгенса – Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн. Френель исключил возможность возникновения обратных вторичных волн и предположил, что если между источником и точкой наблюдения находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии – такая же, как при отсутствии экрана.

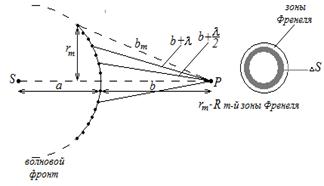
Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т. е. определить закономерности распространения света. В общем случае расчет интерференции вторичных волн довольно сложный и громоздкий, однако, как будет показано ниже, для некоторых случаев нахождение амплитуды результирующего колебания осуществляется алгебраическим суммированием.

Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину. Впервые были описаны в 1675 году И. Ньютоном [1] .

Видео:Интерференция в тонких плёнках и кольца НьютонаСкачать

Содержание

Видео:Опыты по физике. Кольца НьютонаСкачать

Описание [ править | править код ]

Интерференционная картина в виде колец возникает при отражении света от двух поверхностей, одна из которых плоская, а другая имеет относительно большой радиус кривизны и соприкасается с первой (например, стеклянная пластинка и плосковыпуклая линза). Если на такую систему в направлении, перпендикулярном плоской поверхности, падает пучок монохроматического света, то световые волны, отражённые от каждой из упомянутых поверхностей, интерферируют между собой. Сформированная таким образом интерференционная картина состоит из наблюдающегося в месте соприкосновения поверхностей тёмного кружка и окружающих его чередующихся между собой светлых и тёмных концентрических колец [2] .

Видео:Задача про кольца НьютонаСкачать

Классическое объяснение явления [ править | править код ]

Во времена Ньютона из-за недостатка сведений о природе света дать полное объяснение механизма возникновения колец было крайне трудно. Ньютон установил связь между размерами колец и кривизной линзы; он понимал, что наблюдаемый эффект связан со свойством периодичности света, но удовлетворительно объяснить причины образования колец удалось лишь значительно позже Томасу Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда монохроматическая волна падает почти перпендикулярно на плосковыпуклую линзу.

Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны, то есть у них одинаковые длины волн, а разность их фаз постоянна. Разность фаз возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстаёт от первой на целое число длин волн, то, складываясь, волны усиливают друг друга.

Δ = m λ — max,

где m — любое целое число, λ — длина волны.

Напротив, если вторая волна отстаёт от первой на нечётное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах, и волны гасят друг друга.

Δ = ( 2 m + 1 ) λ 2 > — min,

где m — любое целое число, λ — длина волны.

Для учёта того, что в разных веществах скорость света различна, при определении положений минимумов и максимумов используют не разность хода, а оптическую разность хода (разность оптических длин пути).

Если n r — оптическая длина пути, где n — показатель преломления среды, а r — геометрическая длина пути световой волны, то получаем формулу оптической разности хода:

n 2 r 2 − n 1 r 1 = Δ . r_ -n_ r_ =Delta .>

Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами тёмных колец Ньютона. Необходимо также учитывать тот факт, что при отражении световой волны от оптически более плотной среды фаза волны меняется на π ; этим объясняется тёмное пятно в точке соприкосновения линзы и плоскопараллельной пластины. Линии постоянной толщины воздушной прослойки под сферической линзой представляют собой концентрические окружности при нормальном падении света, при наклонном — эллипсы.

Радиус k-го светлого кольца Ньютона (в предположении постоянного радиуса кривизны линзы) в отражённом свете выражается следующей формулой:

r k = ( k − 1 2 ) λ R n , =
ight) >>>,>

где R — радиус кривизны линзы, k = 1 , 2 , . . . , λ — длина волны света в вакууме, n — показатель преломления среды между линзой и пластинкой.

Радиус k-го тёмного кольца Ньютона в отражённом свете определяется в соответствии с формулой:

r k = k λ R n , = >>>,>

Видео:Лабораторная работа по общей физике: кольца НьютонаСкачать

Использование [ править | править код ]

Кольца Ньютона используются для измерения радиусов кривизны поверхностей, для измерения длин волн света и показателей преломления. В некоторых случаях (например, при сканировании изображений на плёнках или оптической печати с негатива) кольца Ньютона представляют собой нежелательное явление.

Используются в физиологии. Подсчёт форменных элементов производится после притирания покровного стекла и камеры Горяева до появления колец Ньютона [3] .