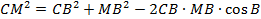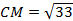О чем эта статья:
- Формулировка и доказательство теоремы косинусов
- Формулировка теоремы для каждой из сторон треугольника
- Косинусы углов треугольника
- Определение угла с помощью косинуса
- Рассмотрение пределов изменения cos α и sin α
- Примеры решения задач
- Косинус b решение треугольников
- Решение прямоугольных треугольников
- Решение произвольных треугольников
- Решение треугольников
- Корзина
- Решение треугольников через синус и косинус угла
- 💥 Видео
Видео:9 класс, 15 урок, Решение треугольниковСкачать

Формулировка и доказательство теоремы косинусов
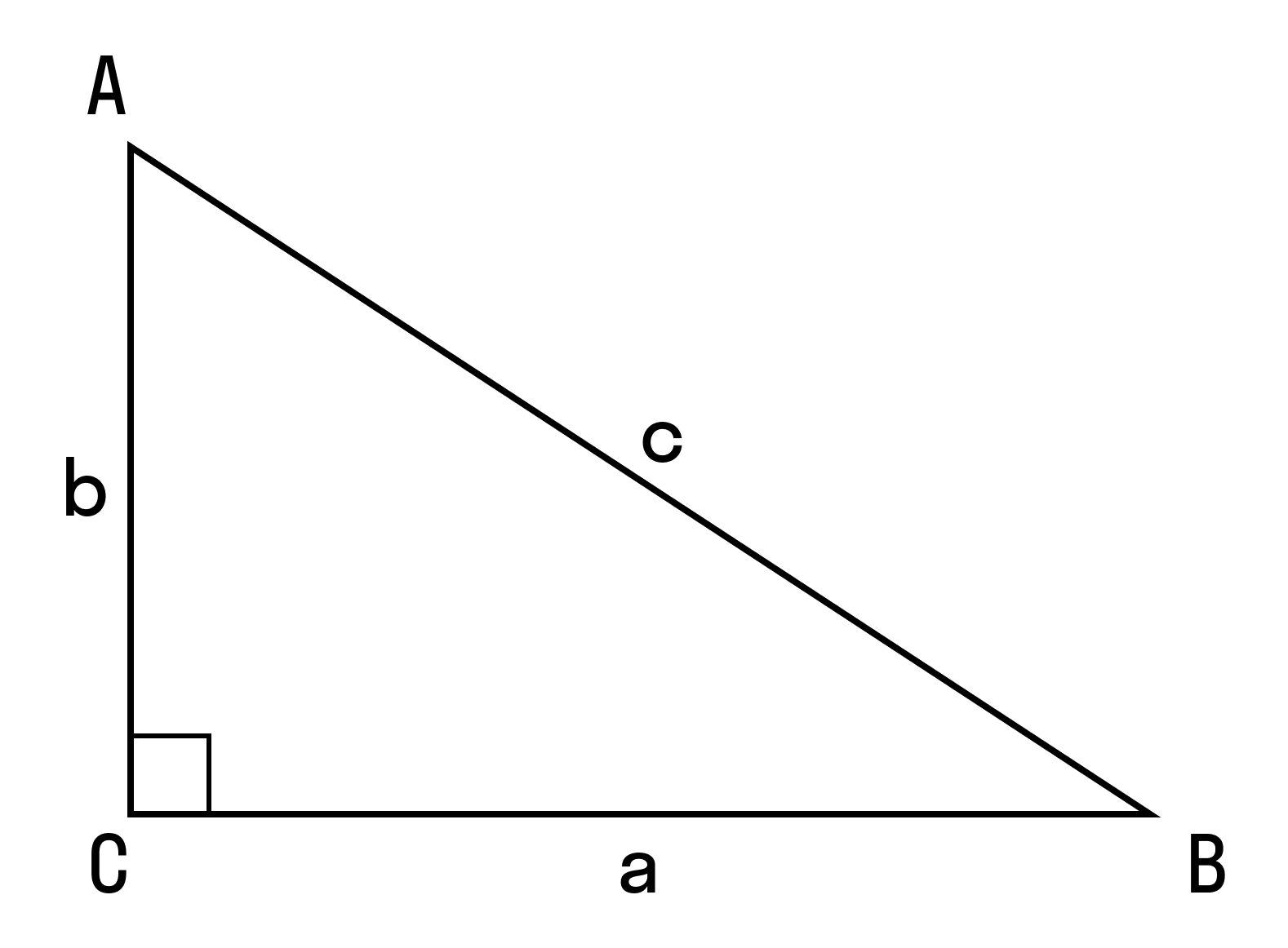
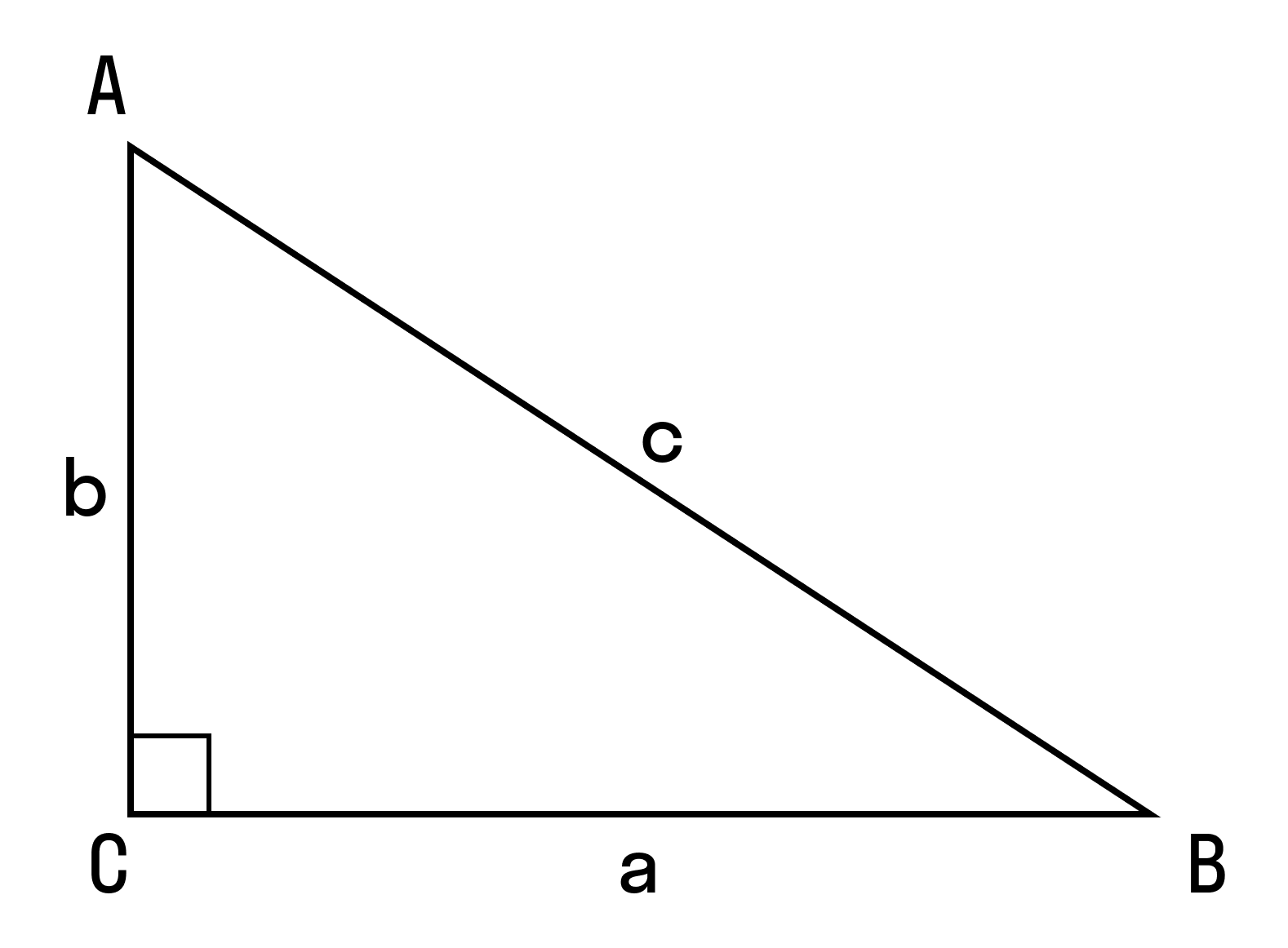
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
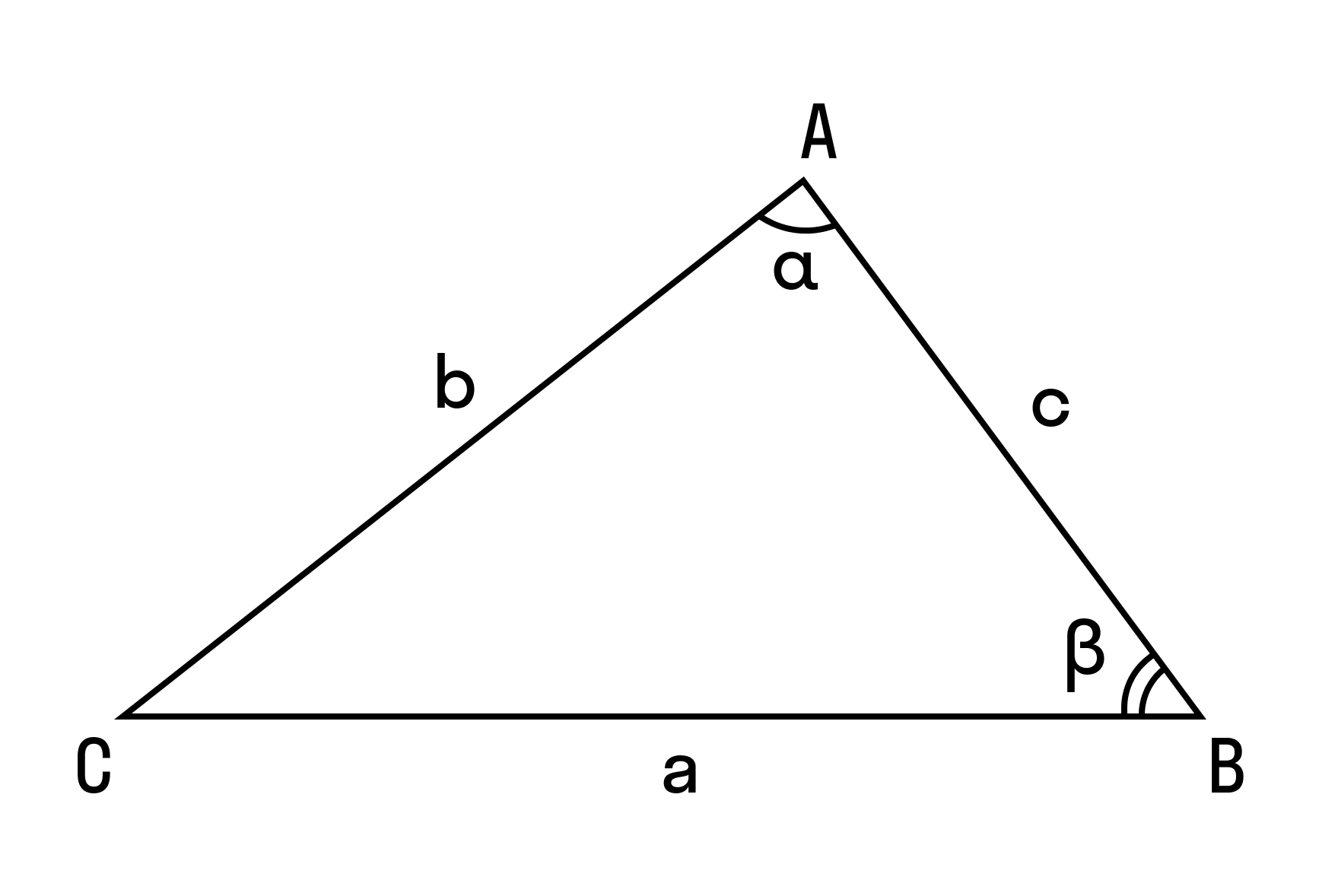
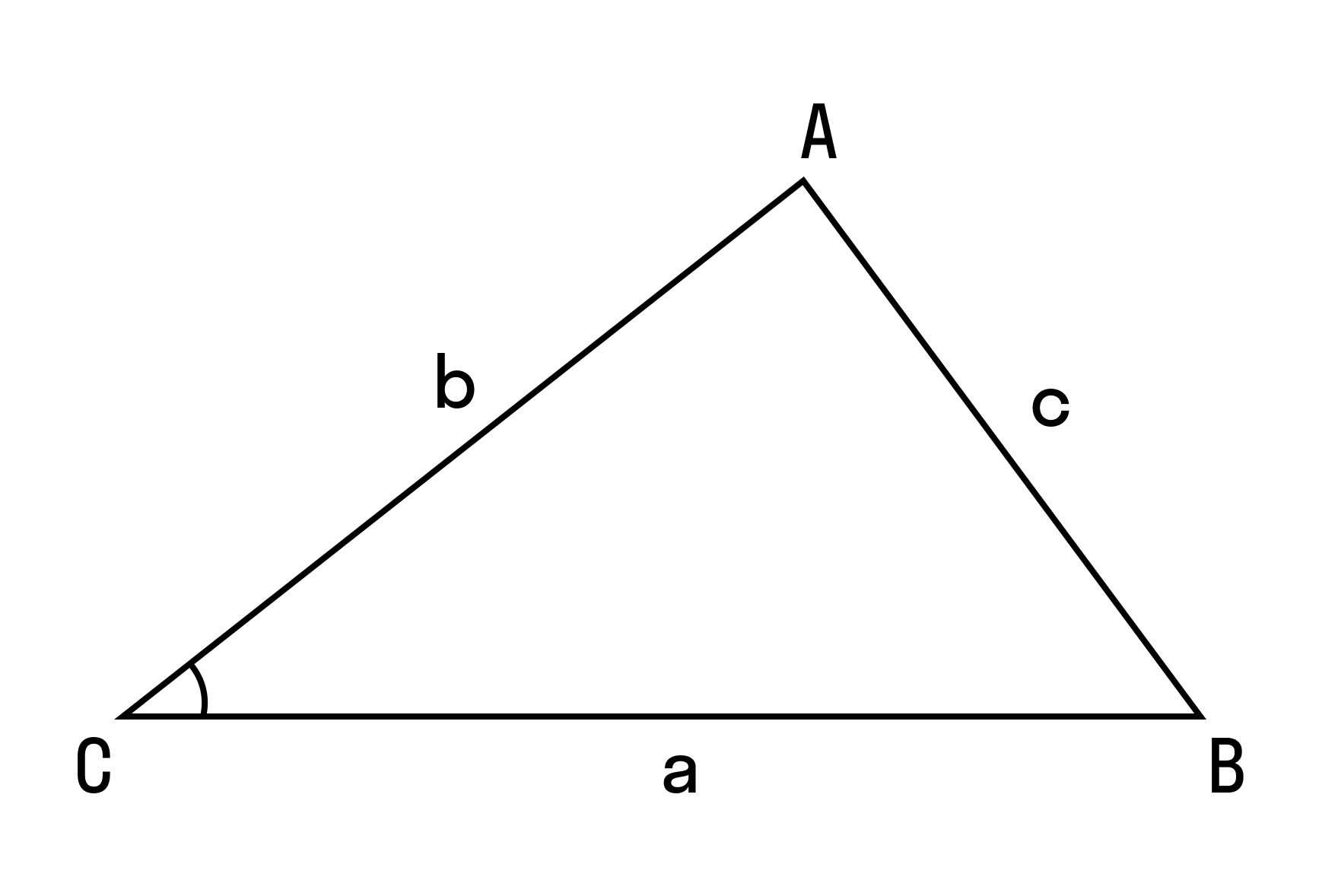
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 — a 2
Сформулируем еще одно доказательство теоремы косинусов.
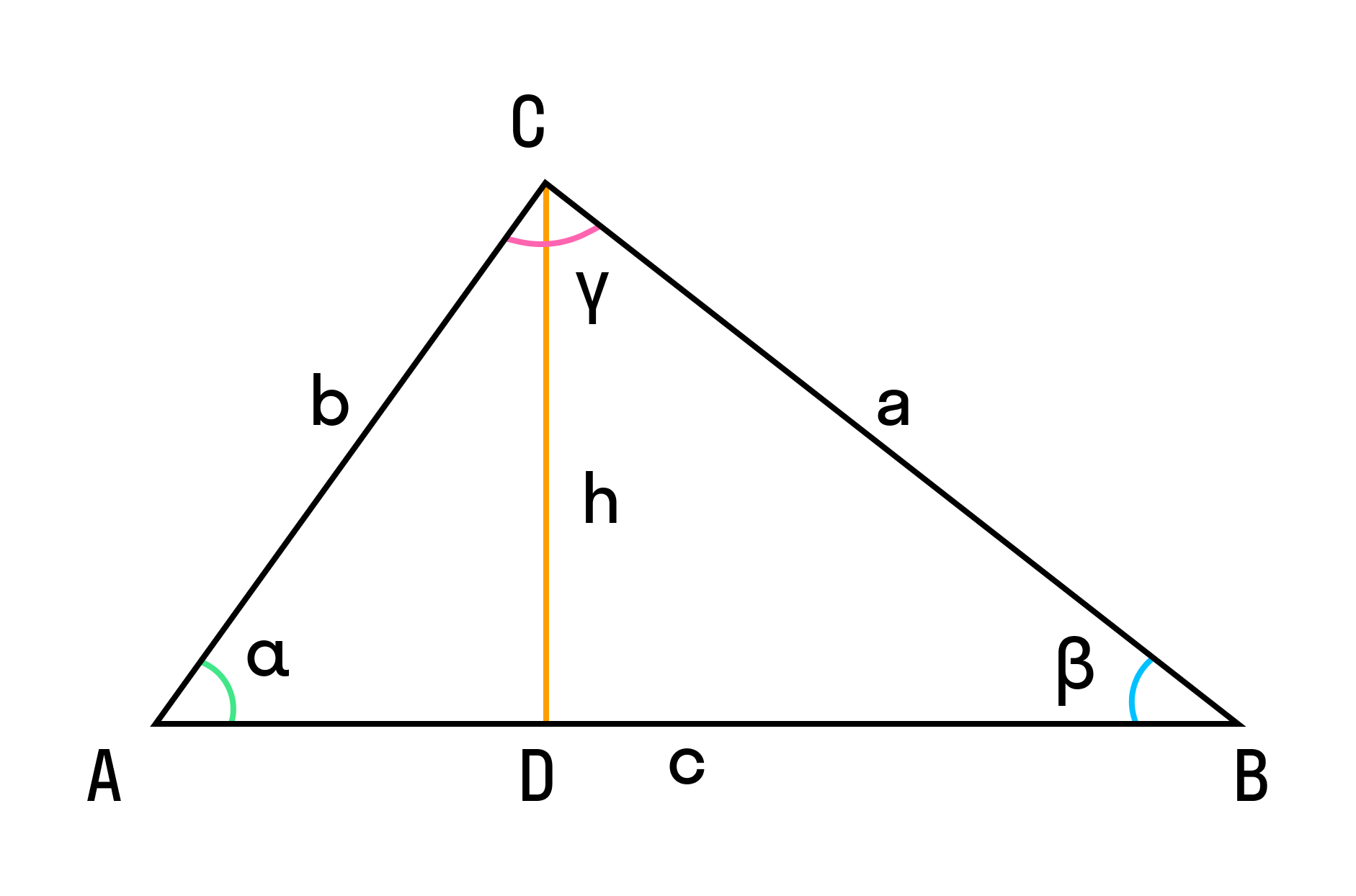
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 — (b × cos α) 2
- h 2 = a 2 — (c – b × cos α) 2
Приравниваем правые части уравнений:
- b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2
- a 2 = b 2 + c 2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 — 2ac × cos β;
- c 2 = a 2 + b 2 — 2ab × cos γ.
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 — 2bc cos α
b 2 = c 2 + a 2 — 2ca cos β
c 2 = a 2 + b 2 — 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Видео:9 класс. Геометрия. Решение треугольниковСкачать

Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Видео:Геометрия 9 класс (Урок№17 - Решение треугольников. Измерительные работы.)Скачать

Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α
Видео:Теорема синусов и теорема косинусов а также РЕШЕНИЕ ТРЕУГОЛЬНИКОВСкачать

Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
Из треугольника СМВ по теореме косинусов найдём СМ:
Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°. Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать Ключевые слова: треугольник, угол, косинус, прямоугольный треугольник, теорема косинусов, теорема синусов, решение треугольников Рассмотрим прямоугольный треугольник ABC. В нем Для решения произвольных треугольников существует теорема косинусов и теорема синусов. Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. Теорема синусов позволяет по двум сторонам и углу, лежащему против одной из них (или по стороне и двум углам) вычислить остальные элементы треугольника. Видео:№1025. С помощью теорем синусов и косинусов решите треугольник ABC, если:Скачать Треугольник ΔABC, Как пользоваться онлайн-калькулятором. В форме укажите три значения: одну сторону и 2 дополнительных параметра (например, угол и сторону, два угла или две стороны). Заполните поле «Текст с картинки». Нажмите «Решить». Теоретический урок для решения задач по теме «Решение треугольников». Бесплатное обучение. Содержание данной онлайн страницы электронного справочника по предмету математики для школьников: Задача 76. стороны треугольника a=10, b=7 Угол Решить треугольник: Угол по сторонам треугольника Sin B = Используя Sin B ≈ 0,6062, находим из тригонометрической таблицы («Четырехзначные математические таблицы» Владимира Модестовича Брадиса) Тогда Используя теорему синусов Ответ: Задача 77. Треугольник ΔABC, стороны треугольника Найти: Угол по сторонам треугольника Т.к. a=b=6,3, то треугольник ΔABC — равнобедренный. Тогда Используя теорему синусов Ответ: Видео:Теорема синусов и теорема косинусовСкачать Задача 78. Найти: угол треугольника Используя теорему синусов Ответ: Задача 79. Найти: углы треугольника Cos B = Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла B Используя формулу теоремы косинусов, находим косинус угла C Cos C = = Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла C Тогда угол A равен Ответ: Задача 80. Найти: угол Т.к. два угла в треугольнике равны Значит, две стороны равны AC=AB=b=c=4,5 Используя теорему синусов находим сторону BC=a Ответ: Задача 81. Треугольник ΔABC, длины трех его сторон Найти: является ли треугольник тупоугольным, прямоугольным, остроугольным 1) Т.к. b=c=4, то треугольник ΔABC — равнобедренный, и, значит, остроугольный. Cos A = Тогда угол A равен 3) Используя формулу теоремы косинусов Cos B = Треугольник ΔABC, два угла и сторона Найти: длину всех сторон треугольника ΔABC = ? Зная размер двух углов в треугольнике ΔABC, находим третий угол Найдем угол Используя теорему синусов AC = (3 • 1) • 2 = 6 (м) Используя теорему синусов AB = Используя теорему синусов Ответ: AB ≈ 3 м, AC = 6 м, BC ≈ 4 м. Три стороны a = 14, b = 18, все углы треугольника ΔABC = ? Т.к. против большего угла лежит большая сторона, то используя формулу теоремы косинусов Cos C = Cos C = Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C Используя формулу теоремы косинусов Cos B = Cos B = Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла B Следовательно, Ответ: Задача 84. Треугольник ΔEKP, сторона и два угла Найти: сторону треугольника PK = ? Используя теорему синусов Sin 115° = Sin (180° — 65°) = Sin 65° Тогда Задача 85. Треугольник ΔABC, две стороны и угол Найти: решить треугольник — определить значение стороны и двух углов (a, Используя формулу теоремы косинусов a = Используя формулу теоремы косинусов Cos C = Cos C = Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C Следовательно, Ответ: a ≈ 13,8 ; РЕШЕНИЕ ТРЕУГОЛЬНИКОВ. Контрольная № 1 Геометрия 9 класс.Скачать ТРИГОНОМЕТРИЯ с нуля — Синус, косинус, тангенс и котангенс острого углаСкачать Решение задачи с применением теоремы синусовСкачать Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать Решение треугольниковСкачать 9 класс, 13 урок, Теорема синусовСкачать 9 класс. Геометрия. Решение треугольников. Теорема косинусов. Теорема синусов. Урок #2Скачать ТЕОРЕМА КОСИНУСОВ. Задачи на произвольные треугольникиСкачать Теоремы синусов и косинусов | Ботай со мной #029 | Борис ТрушинСкачать 8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать 9 класс, 14 урок, Теорема косинусовСкачатьКосинус b решение треугольников
Решение прямоугольных треугольников
Решение произвольных треугольников
См. также:
Площадь треугольника, Прямоугольный треугольник, Равнобедренный треугольник, Равносторонний треугольникРешение треугольников
Корзина

a = BC, b = AC, c = AB — стороны треугольника,





















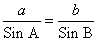

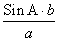

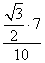

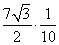

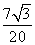





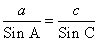

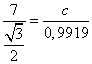



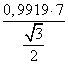

















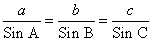

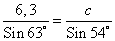



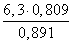

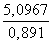




Решение треугольников через синус и косинус угла











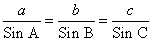

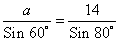



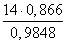

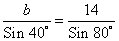



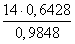











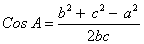

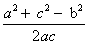

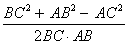

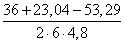

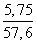



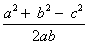

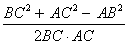

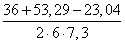























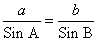





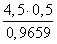


1) a=5 , b=c=4 


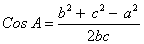

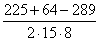

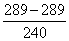



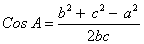

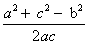

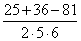

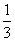














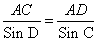

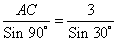













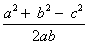

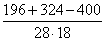

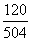



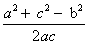

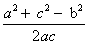

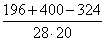

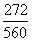
















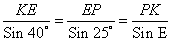



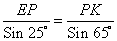



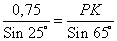




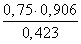







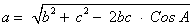

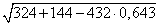

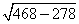

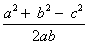

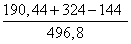

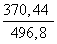








💥 Видео