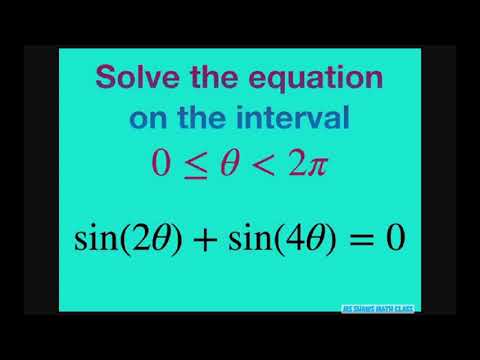Sin2x больше или равно 0 на окружности (4 видео)

Sin2x больше или равно 0 на окружности

Содержание

Шаг 1. Введите неравенство
Решение
Где учитесь?
Решение задач по математике онлайн
Калькулятор онлайн. Решение тригонометрических неравенств.
Немного теории.
Тригонометрические неравенства
Неравенства вида ( sin x > a ) и ( sin x
Неравенства вида ( cos x > a ) и ( cos x
Неравенства вида ( tg ;x > a ) и ( tg ;x
Неравенства вида ( ctg ;x > a ) и ( ctg ;x
Решение тригонометрических неравенств
Здравствуй, уважаемый посетитель!
🌟 Видео

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Шаг 1. Введите неравенство

Укажите решение неравенства: sin(2*x)>0 (множество решений неравенства)

Решение

Дано неравенство:
$$sin > 0$$
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$sin = 0$$
Решаем:
Дано уравнение
$$sin = 0$$
— это простейшее тригонометрическое ур-ние

Получим:
$$sin = 0$$
Это ур-ние преобразуется в
$$2 x = 2 pi n + operatorname$$
$$2 x = 2 pi n — operatorname + pi$$
Или
$$2 x = 2 pi n$$
$$2 x = 2 pi n + pi$$
, где n — любое целое число
Разделим обе части полученного ур-ния на
$$2$$
$$x_ = pi n$$
$$x_ = pi n + frac$$
$$x_ = pi n$$
$$x_ = pi n + frac$$
Данные корни
$$x_ = pi n$$
$$x_ = pi n + frac$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_ 0$$
$$sin<left (2 left(pi n + — fracright) right )> > 0$$

Тогда
$$x pi n wedge x

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Где учитесь?

Для правильного составления решения, укажите:

Видео:Как решать тригонометрические неравенства?Скачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Тригонометрические уравнения sin2x=√2/2; cos x/3=-1/2Скачать

Калькулятор онлайн.
Решение тригонометрических неравенств.

Этот математический калькулятор онлайн поможет вам решить тригонометрическое неравенство. Программа для решения тригонометрического неравенства не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое неравенство
Решить неравенство

Видео:Тригонометрическое неравенство, которое можно решить очень просто на тригонометрической окружностиСкачать

Немного теории.

Видео:Решить тригонометрические неравенства sinxСкачать

Тригонометрические неравенства

Видео:Область определения тригонометрических функцийСкачать

Неравенства вида ( sin x > a ) и ( sin x

Пусть дано простейшее неравенство ( sin x > a ).
1) При (-1 1 ) решением неравенства является любое действительное число: ( x in mathbb )
3) При (а = 1 ) решением неравенства является любое действительное число, отличное от ( frac + 2pi k, ; k in mathbb )
4) При (а leqslant -1 ) неравенство не имеет решений.

Видео:✓ Тригонометрия: с нуля и до ЕГЭ | #ТрушинLive #030 | Борис ТрушинСкачать

Неравенства вида ( cos x > a ) и ( cos x

Пусть дано простейшее неравенство ( cos x > a ).
1) При (-1 1) решением неравенства является любое действительное число: ( x in mathbb )
3) При (a leqslant -1) неравенство не имеет решений.
4) При (a = 1) решением неравенства является любое действительное число, отличное от ( 2pi k, ; k in mathbb )

Видео:Solve: sin 2x - cos x = 0Скачать

Неравенства вида ( tg ;x > a ) и ( tg ;x

Пусть дано простейшее неравенство ( tg ;x > a ).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом (a in mathbb ) решение неравенства будет таким:
$$ x in left(arctg ;a + pi k; ;; frac + pi k right), ; k in mathbb $$

Пусть дано простейшее неравенство ( tg ;x

Видео:Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Неравенства вида ( ctg ;x > a ) и ( ctg ;x

Пусть дано простейшее неравенство ( ctg ;x > a ).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом (a in mathbb ) решение неравенства будет таким:
$$ x in ( pi k; ;; arcctg ;a + pi k ), ; k in mathbb $$

Пусть дано простейшее неравенство ( ctg ;x

Видео:(sin2x+2sin^2 x)/√(-cosx)=0 Задание 13 Профильный ЕГЭ по математике Исследование ОДЗСкачать

Решение тригонометрических неравенств

ПРИМЕР 1. Решим неравенство ( sin x > frac ).
Так как ( -1 frac ).
Так как ( -1 1 ).
Очевидно, что решение неравенства будет таким:
$$ x in left(frac + pi k; ;; frac + pi kright), ; k in mathbb $$

ПРИМЕР 6. Решим неравенство ( tg ;x frac<sqrt> ).
Очевидно, что решение неравенства будет таким:
$$ x in left( pi k; ;; frac + pi k right), ; k in mathbb $$

ПРИМЕР 8. Решим неравенство ( ctg ;x

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Здравствуй, уважаемый посетитель!

Меня зовут Александр Бабаев. И это мой сайт.Он посвящён не только математике. Вы найдёте здесь много интересных и полезных, я надеюсь, для себя вещей.
Кроме того, что здесь выкладываются интересные задачки, разбираются непонятные моменты и осуществляется помощь в решении трудных задач, на сайте выкладывается фото и видео мероприятий, которые я провожу, в блоге вы найдёте обсуждение различных проблем с которыми я сталкиваюсь и могу поделиться с вами, дорогой посетитель.
Для моих замечательных студентов есть специальный раздел, где они могут посмотреть всё, что им нужно для овладевания курсом математики.
Более того, в специальных разделах я публикую мои рецензии на просмотренные мной фильмы и игры.