По контуру в виде окружности радиусом r течет (8 видео)

По контуру в виде окружности радиусом R течет ток. Определите индукцию магнитного поля в центре этой окружности, если сила тока равна I.

Содержание

Ваш ответ
Похожие вопросы
По контуру в виде окружности радиусом R течет ток. Определите индукцию магнитного поля в центре этой окружности, если сила тока равна I.
Вопрос вызвавший трудности
Ответ подготовленный экспертами Учись.Ru
Теорема о циркуляции вектора индукции магнитного поля
Интегральная форма теоремы о циркуляции
Готовые работы на аналогичную тему
Дифференциальная форма теоремы о циркуляции
📺 Видео

Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать

Ваш ответ

Видео:Урок 287. Индуктивность контура (катушки). Явление самоиндукцииСкачать

По контуру в виде окружности радиусом R течет ток. Определите индукцию магнитного поля в центре этой окружности, если сила тока равна I.

В 17:23 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.

Видео:Лекция 7-4 Законы магнитного поляСкачать

Вопрос вызвавший трудности

Видео:Как решать задачи на нахождение магнитного поля.Скачать

Ответ подготовленный экспертами Учись.Ru

Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: По контуру в виде окружности радиусом R течет ток. Определите индукцию магнитного поля в центре этой окружности, если сила тока равна I.

После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:

ответ к заданию по физике

НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:

Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.

Суворова Рая Леонидовна — автор студенческих работ, заработанная сумма за прошлый месяц 57 486 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию

ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!

Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.

Деятельность компании в цифрах:

Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.

Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.

Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.

Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.

Видео:Билет №27 "Магнитный поток. Взаимоиндукция"Скачать

Теорема о циркуляции вектора индукции магнитного поля

Вы будете перенаправлены на Автор24

Видео:3.237 ир=4.31 кпиСкачать

Интегральная форма теоремы о циркуляции

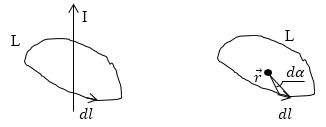
Линии индукции магнитного поля, которое возникает вокруг постоянного тока, который течет по прямолинейному длинному проводнику — концентрические окружности с центрами на линии тока. Интеграл вида $ointlimits_L<overrightarrowdoverrightarrow> $- циркуляция вектора $overrightarrow$ по замкнутому контуру L. Найдем $ointlimits_L<overrightarrowdoverrightarrow>$ по некоторому замкнутому контуру вокруг тока I (рис. 1).

Линии магнитной индукции лежат в плоскостях перпендикулярных линии тока I, контур L выбираем в плоскости одной из линий $overrightarrow.$ Используем рис.1, получим:

Обозначим $left(widehat<overrightarrowdoverrightarrow>right)=alpha $, тогда имеем:

По условию магнитное поле создает бесконечно длинный прямой проводник с током, индукцию поля которого мы знаем, и запишем в точке на расстоянии r от проводника как:

Подставим (3) и (2) в формулу (1), получим:

Теперь найдем циркуляцию вектора магнитной индукции, используя (4), получим:

где использовано то, что для замкнутого контура, который окружает начало координат:

Из полученного результата в (5) видим, что циркуляция вектора магнитной индукции по замкнутому контуру вокруг тока не зависит от вида контура и определена только силой тока. В том случае если контур ток не охватывает, то циркуляция вектора индукции равна нулю.

Тогда теорема о циркуляции для нескольких токов формулируется следующим образом:

Циркуляция индукции магнитного поля постоянных токов по произвольному замкнутому контуру равна алгебраической сумме токов, которые пронизывают этот контур.

Готовые работы на аналогичную тему

В математическом виде данная формулировка выглядит как уравнение:

где через I — обозначают полный ток (алгебраическая сумма всех токов, охватываемых контуром). Теорема о циркуляции еще называется законом полного тока. Надо иметь в виду, что циркуляция вектора $overrightarrow$ по замкнутому контуру равна нулю не только в случае отсутствия токов, которые пронизывают заданный контур, но и если токи текут в противоположных направлениях и в сумме дают ноль. В формуле (7) знак тока учитывается по правилу правого винта. Этот закон мы получили для прямого бесконечного проводника, но он справедлив и для произвольного тока.

Видео:Закон Био Савара Лапласа. Магнитное поле прямого и кругового тока.Скачать

Дифференциальная форма теоремы о циркуляции

Пусть S — поверхность, которую охватывает контур L. Положительная нормаль к поверхности связана с направлением обхода контура L правилом правого винта. Силу полного тока, который течет через поверхность S можно записать как:

где $overrightarrow$ — объёмная плотность тока. В таком случае теорему о циркуляции запишем как:

По теореме Стокса можно записать, что:

Равенство (11) выполняется для любой поверхности, следовательно, подынтегральное выражение также равно нулю:

[rotoverrightarrow-_0overrightarrow=0to rotoverrightarrow=_0overrightarrow left(12right).]

Равенство (12) дифференциальная форма теоремы о циркуляции. Она справедлива для произвольного поля в каждой точке.

Напомним, что теорема о циркуляции в виде (7) и (12) записана для поля в вакууме и стационарных токов.

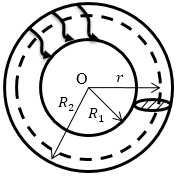
Задание: Тороид имеет каркас в виде тора и на него намотан проводник, по которому течет ток. Магнитное поле данной конфигурации токов сосредоточено в основном внутри тороида. Поле имеет осевую симметрию. Силовые линии магнитного поля тороида представляют собой окружности с центром на оси тороида. Используя теорему о циркуляции, найдите магнитное поле внутри тороида (рис.2) (B(r)). Если сила тока в нем равна I. N — число витков тороида.

В качестве контура циркуляции выберем силовую линию в виде окружности радиуса r (рис.2). Запишем, что циркуляция вектора индукции магнитного поля вдоль выбранной окружности равна:

[ointlimits_L<overrightarrowdoverrightarrow>=B2pi r left(1.1right).]

Тогда теорема о циркуляции предстанет в виде:

где $N$ — число витков с током. Выразим модуль вектора индукции, получим:

Задание: Какова циркуляция вектора индукции вдоль контура, который охватывает токи $I_1=5 A, I_2=6 A$, $I_3=10 A$, если первые два тока текут в одном направлении, третий в противоположном.

По теореме о циркуляции:

Для нашего случая имеем:

Проведем вычисление, получим:

[ointlimits_L<overrightarrowdoverrightarrow>=5+6-10=1 left(Тлcdot мright).]

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 09 02 2021