К двум непересекающимся окружностям разных радиусов (3 видео)

Две окружности на плоскости.
Общие касательные к двум окружностям

Взаимное расположение двух окружностей

Общие касательные к двум окружностям

Формулы для длин общих касательных и общей хорды

Доказательства формул для длин общих касательных и общей хорды

Содержание

Взаимное расположение двух окружностей
Формулы для длин общих касательных и общей хорды двух окружностей
Доказательства формул для длин общих касательных и общей хорды двух окружностей
К двум непересекающимся окружностям разных радиусов
Задача 27559 9.13. Точка пересечения двух общих.
Условие
Все решения
📸 Видео

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Взаимное расположение двух окружностей

Взаимное расположение на плоскости двух окружностей радиусов r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r₁ – r₂ лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

r₁ – r₂ лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов

d r₁ и r₂ с центрами O₁ и O₂ определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей меньше разности их радиусов

d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

Фигура	Рисунок	Свойства
Две окружности на плоскости
Каждая из окружностей лежит вне другой
Внешнее касание двух окружностей
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Каждая из окружностей лежит вне другой

Внешнее касание двух окружностей

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках


Каждая из окружностей лежит вне другой
Расстояние между центрами окружностей больше суммы их радиусов
Внешнее касание двух окружностей
Расстояние между центрами окружностей равно сумме их радиусов
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r₁ – r₂ лежит внутри другой
Внутренняя касательная к двум окружностям
Внутреннее касание двух окружностей
Окружности пересекаются в двух точках
Внешнее касание двух окружностей
Внешнее касание двух окружностей

Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках

Внешнее касание двух окружностей


Каждая из окружностей лежит вне другой

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Формулы для длин общих касательных и общей хорды двух окружностей

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Внутреннее касание двух окружностей

Окружности пересекаются в двух точках

Внешнее касание двух окружностей

Каждая из окружностей лежит вне другой

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Фигура	Рисунок	Формула
Внешняя касательная к двум окружностям
Внутренняя касательная к двум окружностям
Общая хорда двух пересекающихся окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Общая хорда двух пересекающихся окружностей

Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Внешняя касательная к двум окружностям

Внутренняя касательная к двум окружностям

Общая хорда двух пересекающихся окружностей

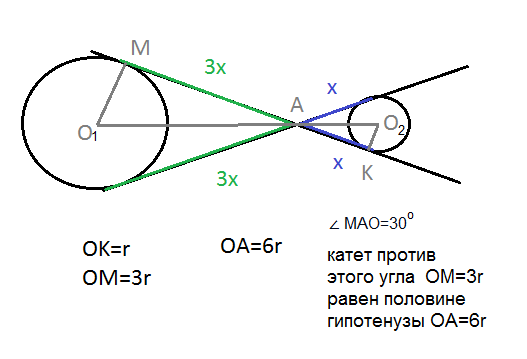
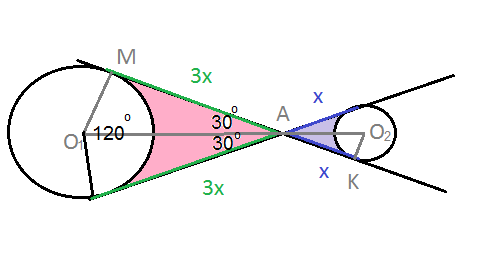
Длина общей хорды двух окружностей вычисляется по формуле

Видео:Внешняя касательная к двум окружностямСкачать

Доказательства формул для длин общих касательных и общей хорды двух окружностей

Утверждение 1 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле

что и требовалось доказать.

Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле

что и требовалось доказать.

Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r₁ и r₂ равно d , то длина общей хорды AB этих окружностей вычисляется по формуле

Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,

Видео:ЕГЭ 2014 математика C-4Скачать

К двум непересекающимся окружностям разных радиусов

К двум непересекающимся окружностям равных радиусов проведены две параллельные общие касательные. Окружности касаются одной из этих прямых в точках A и B Через точку C, лежащую на отрезке AB, проведены касательные к этим окружностям, пересекающие вторую прямую в точках D и E, причём отрезки CA и CD касаются одной окружности, а отрезки CB и CE — другой.

а) Докажите, что периметр треугольника CDE вдвое больше расстояния между центрами окружностей.

б) Найдите DE, если радиусы окружностей равны 5, расстояние между их центрами равно 18, а AC = 8.

а) Пусть O₁ — центр окружности, которая касается отрезка CD, O₂ — центр окружности, которая касается отрезка CE, R — радиус окружностей. Окружность с центром O₁ касается отрезка CD в точке K, а прямой DE в точке M; окружность с центром O₂ касается отрезка CE в точке L, а прямой DE в точке N (рис. 1).

Тогда периметр треугольника CDE

б) Точка O₁ лежит на биссектрисах углов MDC и ACD (рис. 2), следовательно,

В прямоугольном треугольнике CO₁D имеем:

Аналогично, Получаем, что

Критерии оценивания выполнения задания

Баллы

Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)

Получен обоснованный ответ в пункте б)

имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Видео:Внутренняя касательная к двум окружностямСкачать

Задача 27559 9.13. Точка пересечения двух общих.

Условие

9.13. Точка пересечения двух общих касательных к двум непересекающимся окружностям, меньшая из которых имеет радиус r, лежит на линии их центров на расстоянии 6r от центра большей окружности и делит отрезок касательной между точками касания в отношении 1:3. Найдите площадь фигуры, состоящей из двух частей, ограниченных касательными и большими дугами окружностей.

Все решения

Из подобия треугольников МО_(1)А и КО_(2)А
О_(1)М=3r- радиус большего круга.
АО_(2)=2r

В прямоугольном треугольнике катет против угла в 30 градусов равен половине гипотенузы и обратно.
Катет О_(1)М=3r
Гипотенуза О_(1)А=6r
Значит, ∠ МАО = 30 градусов, вертикальные углы между касательными 60 градусов.

Cм. рис. 2
S ( фигуры)=S(большого круга)+S(малого круга)+S(криволинейного треугольника розового цвета)+
S( криволинейного треугольника сиреневого цвета)

S(большого круга)=Pi*(3r)^2=9Pir^2
S(малого круга)=Pi*r^2=Pir^2
S(криволинейного треугольника розового цвета)=2*S( Δ О_(1)МА)- s( большого сектора с углом в 120 градусов)=
=2*(1/2)*3r*6r*sin60 градусов -(1/3)*Pi*(3r)^2=
=9r^2sqrt(3)-3Pir^2
S( криволинейного треугольника сиреневого цвета) =
2S(ΔО_(2)АК)-s(малого сектора с углом в 120 градусов)=
=2*(1/2)*r*2r*sqrt(3)/2-(1/3)Pi*r^2=r^2sqrt(3)-(Pir^2/3)

О т в е т. 9Pir^2 + Pir^2 + (9r^2sqrt(3)-3Pir^2)+(r^2sqrt(3)-(Pir^2/3))=(20/3)Pir^2+10r^2sqrt(3)