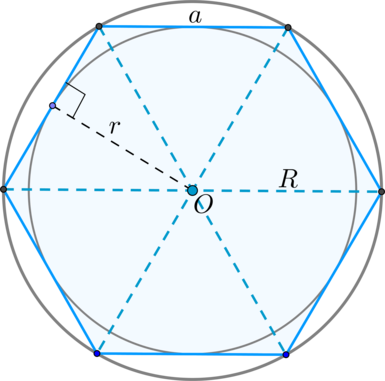
Правильный шестиугольник вписанный в окружность. К вашему вниманию типичная задача, которая встречается в школьном курсе математики. Сначала небольшое теоретическое отступление. Информацию о шестиугольнике и окружности можно посмотреть здесь и тут.
Известно, что в правильном шестиугольнике расстояния от центра до его вершин равны, также это расстояние равно стороне шестиугольника. То есть правильный шестиугольник состоит как бы из шести равносторонних треугольников «сложенных» друг с другом.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

ГДЗ по геометрии 9 класс Атанасян Л. С.
Задача 1097. Найдите отношение площадей двух правильных шестиугольников – вписанного в окружность и описанного около неё.
Как правило, когда дано такое условие большинство ребят привыкли строить эскиз следующим образом:
*Конечно, можно построить диагонали и высоты образованных равносторонних треугольников. Далее обозначить сторону описанного шестиугольника, например, за «х» и вычислять их площади.
Мы поступим следующим образом: повернём вписанный шестиугольник по часовой стрелке на 30 градусов и разобьём (диагоналями) на 6 равносторонних треугольников:
Видно, что сторона вписанного шестиугольника равна высоте описанного. Кроме того, очевидно, что рассматриваемые шестиугольники подобны. Вспомним свойства подобия фигур:
=> отношение сторон подобных фигур равно коэффициенту подобия, то есть
=> отношение площадей подобных фигур равно квадрату коэффициента подобия, то есть
Для того чтобы вычислить отношение площадей шестиугольников нам достаточно найти отношение площадей двух равносторонних треугольников (маленького и большого):
*Как уже сказано: сторона маленького треугольника равна высоте большого.
Мы знаем, что в равностороннем треугольнике со стороной «х» его высота равна
*Это несложное вычисление, можно использовать теорему Пифагора.
Значит отношение сторон оговоренных треугольников будет равно:
Мы получили коэффициент подобия.
Таким образом, отношение площадей треугольников (малого и большого), а значит и вписанного и описанного шестиугольников будет равно квадрату этого коэффициента:
Ещё вариант решения!
Мы можем найти отношение площадей оговоренных выше равносторонних треугольников. Используем формулу площади треугольника:
Сторону большего треугольника принимаем за х, следовательно площадь будет равна:
Сторона меньшего треугольника будет равна (х√3)/2, тогда его площадь:
Отношение площади меньшего к площади большего равно:
Итог: мы построили эскиз, вычислили отношение сторон шестиугольников (отношение сторон равносторонних треугольников), далее использовали свойство подобия.
*Комментарий: не смотря на то что объяснение решения изложено несколько ёмко, на самом деле сам процесс вычисления очень прост и при понимании осуществляется в течение минуты. Здесь важна сама идея решения, а именно: использование свойства подобия фигур. И, безусловно, время затраченное на поиск результата будет значительно меньше, чем если бы мы вычисляли отношение площадей другим способом.
Дополнение! Важен один момент: необходимо внимательно прочитать условие. Здесь сказано, что необходимо найти отношение площадей вписанного и описанного шестиугольника. Если же будет стоять вопрос о нахождении отношения площади описанного и вписанного шестиугольника, то результат будет другой. Подробнее:
Отношение сторон большого и малого треугольников будет равно:
Это есть коэффициент подобия. Значит его квадрат будет равен:
То есть отношение площадей в этом случае будет равно 4/3.
Материал предоставил репетитор по математике, ведущий курсов ЕГЭ по математике и информатике в городе Челябинск Евгений Маслов .
Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Найдите отношение площади правильного шестиугольника, описанного около окружности, к площади правильного шестиугольника, вписанного в эту окружность.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Ваш ответ
Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

решение вопроса
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,061
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Правильный шестиугольник и его свойства
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac 4cdot 180^circ=90^circ) ;
каждый угол правильного шестиугольника равен (dfrac6cdot 180^circ=120^circ) .
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfracn\ r&=Rcdot cosdfracn end]
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: (a=R) .
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны (120^circ) .
4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt>a^2) .
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac) .
🎦 Видео
Задача 6 №27917 ЕГЭ по математике. Урок 134Скачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

ЕГЭ 2022 математика задача 4 вариант 2Скачать

Свойства правильного шестиугольника. Сравнение площадей. Разбор задачи из стереометрии.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Задание № 1097 - Геометрия 9 класс (Атанасян)Скачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

ЕГЭ Задание 16 Правильный шестиугольникСкачать
№ 201-300 - Геометрия 9 класс МерзлякСкачать

Геометрия - Построение шестиугольникаСкачать