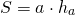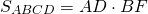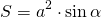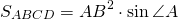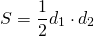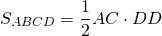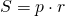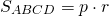- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
- Ромб. Формулы, признаки и свойства ромба
- Признаки ромба
- Основные свойства ромба
- Сторона ромба
- Формулы определения длины стороны ромба:
- Диагонали ромба
- Формулы определения длины диагонали ромба:
- Периметр ромба
- Формула определения длины периметра ромба:
- Площадь ромба
- Формулы определения площади ромба:
- Окружность вписанная в ромб
- Формулы определения радиуса круга вписанного в ромб:
- Площадь ромба
- 🔍 Видео
Видео:Площадь ромба. Легче понять...Скачать
We are checking your browser. mathvox.ru
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d553fb689ff1672 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Ромб. Формулы, признаки и свойства ромба
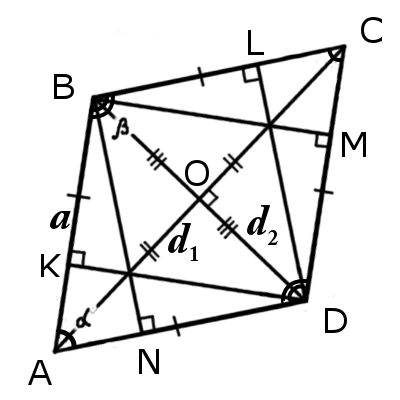 | 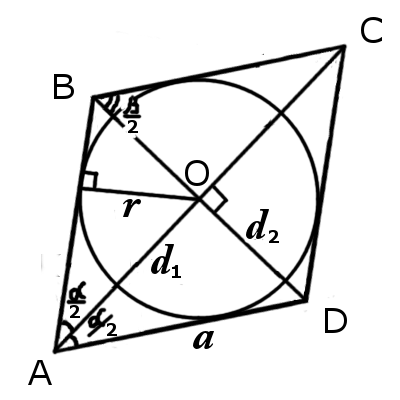 |
| Рис.1 | Рис.2 |
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
AC 2 + BD 2 = 4AB 2
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
| a = | S |
| ha |
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
4. Формула стороны ромба через две диагонали:
| a = | √ d 1 2 + d 2 2 |
| 2 |
5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):
| a = | d 1 |
| √ 2 + 2 cosα |
| a = | d 2 |
| √ 2 — 2 cosβ |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
8. Формула стороны ромба через периметр:
| a = | Р |
| 4 |
Видео:ГЕОМЕТРИЯ 8 класс: Площадь ромба | ВидеоурокСкачать

Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 1 = a √ 2 — 2 · cosβ
d 2 = a √ 2 + 2 · cosβ
d 2 = a √ 2 — 2 · cosα
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
| S = | 1 | d 1 d 2 |
| 2 |
5. Формула площади ромба через синус угла и радиус вписанной окружности:
| S = | 4 r 2 |
| sinα |
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Видео:Площадь ромба - половина произведения его диагоналейСкачать
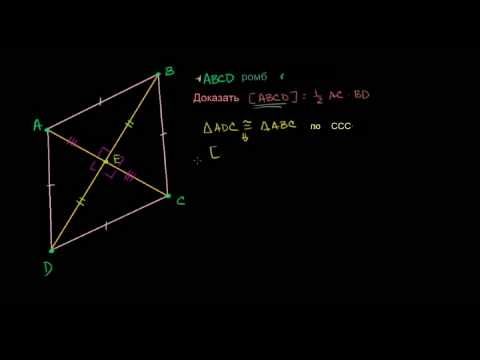
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
| r = | h |
| 2 |
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
| r = | S |
| 2 a |
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
| r = | √ S · sinα |
| 2 |
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
| r = | d 1 · d 2 |
| 4 a |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Площадь ромба
Площадь ромба можно найти по формулам для нахождения площади параллелограмма. С учётом свойств ромба, некоторые из этих формул меняют свой вид.
I. Площадь ромба по стороне и высоте
Площадь ромба равна произведению стороны ромба и его высоты.
Формула для нахождения площади ромба по стороне и высоте не отличается от соответствующей формулы площади параллелограмма:

Так как все стороны ромба равны и все его высоты равны, для нахождения площади можно брать любую сторону и любую высоту.
II. Площадь ромба по стороне и углу
Площадь ромба равна произведению квадрата его стороны на синус угла.
Формула для нахождения площади ромба через сторону и угол:

Так как ∠D=180-∠A, sin∠D=sin(180-∠A)=sin∠A, то для нахождения площади можно брать синус любого угла.
III. Площадь ромба через его диагонали
Площадь ромба равна половине произведения его диагоналей.
Формула для нахождения площади ромба по его диагоналям
по сравнению с соответствующей формулой площади параллелограмма упрощается (так как диагонали ромба взаимно перпендикулярны, а синус прямого угла равен единице).

IV. Площадь ромба через радиус вписанной окружности
Площадь ромба равна произведению его полупериметра на радиус вписанной окружности.
Формула для нахождения площади ромба через радиус вписанной окружности
аналогов среди формул для нахождения площади параллелограмма не имеет (поскольку из всех параллелограммов окружность можно вписать только в ромб и квадрат).

Так как полупериметр ромба равен p=2a, формулу можно записать в виде
🔍 Видео
Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Задача 6 №27914 ЕГЭ по математике. Урок 132Скачать

112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Радиус описанной окружностиСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

Геометрия 6. Радиусы вписанной и описанной окружностей.Скачать