Площадь основания окружности конуса формула (5 видео)

Нахождение площади поверхности конуса: формула и задачи

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого кругового конуса (боковую, полную и основания), а также разберем примеры решения задач для закрепления материала.

Содержание

Формула вычисления площади конуса
1. Боковая поверхность
2. Основание
3. Полная площадь
Примеры задач
Площадь основания окружности конуса формула
Как найти площадь поверхности конуса: боковую, основания, полную
Фигура конус
Найти площадь поверхности конуса через:
Площадь куба
Формула площади боковой поверхности конуса
Площадь боковой поверхности конуса через его радиус и направляющую
Площадь прямоугольного параллелепипеда
🎦 Видео

Видео:Усеченный конус. 11 класс.Скачать

Формула вычисления площади конуса

1. Боковая поверхность

Площадь (S) боковой поверхности конуса равняется произведению числа π на радиус основания и на длину образующей.

Образующая ( l ) соединяет вершину конуса и границу основания, другими словами, точку на окружности.

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

Основанием конуса является круг, площадь которого вычисляется так:

Учитывая то, что диаметр круга равняется двум его радиусам ( d = 2R ), данную формулу можно представить в виде:

3. Полная площадь

Для вычисления суммарной площади конуса следует сложить площади боковой поверхности и основания:

Видео:11 класс, 17 урок, Площадь поверхности конусаСкачать

Примеры задач

Задание 1
Вычислите площадь боковой поверхности конуса, если известно, что его радиус равен 16 см, а длина образующей – 5 см.

Решение:
Используем соответствующую формулу с известными нам величинами:
S = 3,14 ⋅ 16 см ⋅ 5 см = 251,2 см 2 .

Задание 2
Высота конуса равна 4 см, а его радиус – 3 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если рассмотреть конус в сечении, то можно заметить, что его высота, радиус и образующая представляют собой прямоугольный треугольник. Следовательно, воспользовавшись теоремой Пифагора, можно найти длину образующей (является гипотенузой):
l 2 = (4 см) 2 + (3 см) 2 = 25 см 2 .
l = 5 см.

Осталось только использовать найденное и известные по условиям задачи значения, чтобы рассчитать площадь:
S = 3,14 ⋅ 3 см ⋅ (5 см + 3 см) = 75,36 см 2 .

Видео:Конус. 11 класс.Скачать

Площадь основания окружности конуса формула

Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники . На рисунке 168 осевым сечением конуса является треугольник ABP ( АР = ВР ). Угол АPВ называют углом при вершине осевого сечения конуса .

Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.

Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP ).

Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).

Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением .

Если сечением цилиндрической поверхности плоскостью может быть либо окружность, либо эллипс, либо две параллельные прямые, то сечением конической поверхности плоскостью может быть либо окружность (секущая плоскость перпендикулярна оси конической поверхности вращения и не проходит через её вершину, рис. 171, a ), либо эллипс (секущая плоскость не перпендикулярна оси конической поверхности и пересекает все её образующие, рис. 171, б ), либо парабола (секущая плоскость параллельна только одной образующей конической поверхности, рис. 171, в ), либо гипербола (секущая плоскость параллельна оси конической поверхности, рис. 171, г ), либо пара пересекающихся прямых (секущая плоскость проходит через вершину конической поверхности, рис. 171, д ). Поэтому невырожденные кривые второго порядка — окружность, эллипс, параболу и гиперболу называют коническими сечениями или коротко — кониками .

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.

 ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60 ° ; б) в 90 ° . Найти площадь сечения.

Решени е. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.

Хорда АВ окружности основания стягивает дугу в 60 ° , значит, △ AOB — правильный и АВ = R .

Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S △ ABP = АВ • РC. Имеем: ОР = R (по условию); в △ A OB : ОС = ; в △ ОСР : CP = = .

Тогда S △ ABP = АВ • РС = .

Ответ: а) .

18.3. Касательная плоскость к конусу

Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.

Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.

Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.

18.4. Изображение конуса

Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).

Для достижения наглядности изображения невидимые линии изображают штрихами.

Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.

18.5. Развёртка и площадь поверхности конуса

Пусть l — длина образующей, R — радиус основания конуса с вершиной Р .

Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a ), то получим развёртку поверхности конуса (рис. 176, б ), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса ; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):

α = .

За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.

Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле

S бок = α • l 2 , (1)

где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = , получаем:

Таким образом, доказана следующая теорема.

Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼

Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.

S кон = π Rl + π R 2 . (3)

Следствие. Пусть конус образован вращением пря м оугольного треугольника ABC вокруг катета АС (рис. 177). Тогда S бок = π • BC • АВ. Если D — середина отрезка АВ, то AB = 2 AD, поэтому

S бок = 2 π ВС • AD. (4)

Проведём DE ⟂ АB ( E ∈ l = AС ) . Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А ) имеем

= ⇒ BC • AD = DE • АС. (5)

Тогда соотношение (4) принимает вид

S бок = (2 π • DE ) • AC, (6)

т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.

Это следствие будет использовано в п. 19.7.

18.6. Свойства параллельных сечений конуса

Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.

Доказательств о. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α , параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).

Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β , α || β , то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O 1 = α ∩ РО. Обозначим этот круг F 1 .

Рассмотрим гомотетию с центром P, при которой плоскость β основания данного конуса отображается на параллельную ей плоскость α (при гомотетии плоскость, не проходящая через центр гомотетии, отображается на параллельную ей плоскость).

Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия отображает основание F конуса на его параллельное сечение — круг F 1 , при этом центр О основания отображается на центр О 1 круга F 1 (почему?). Кроме того, если РХ — произвольная образующая конуса, где Х — точка окружности основания, то при гомотетии точка X отображается на точку X 1 = РX ∩ α . Учитывая, что отношение длин гомотетичных отрезков равно коэффициенту гомотетии, получаем:

= = k, (*)

где k — коэффициент гомотетии , т. е. параллельное сечение конуса делит его образующие и высоту на пропорциональные части.

А поскольку гомотетия является подобием, то круг F 1 , являющийся параллельным сечением конуса, подобен его основанию.

Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO 1 : Р О , где РO 1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то

S сечен : S основ = k 2 = : PO 2 .

18.7. Вписанные в конус и описанные около конуса пирамиды

Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.

Для построения изображения правильной пирамиды, вписанной в конус:

— строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;

— соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;

— выделяют видимые и невидимые (штрихами) линии изображаемых фигур.

На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:

— прямоугольный треугольник (см. рис. 179);

Видео:Цилиндр, конус, шар, 6 классСкачать

Как найти площадь поверхности конуса: боковую, основания, полную

Видео:Геометрия 11 класс (Урок№7 - Конус.)Скачать

Фигура конус

Чтобы понять, как найти образующую конуса, следует дать представление об этой фигуре. Круглым прямым конусом называют фигуру вращения прямоугольного треугольника вокруг одного из его катетов. Рисунок ниже демонстрирует процесс вращения.

Полученная пространственная фигура имеет следующие характеристики:

Сторона AB треугольника является высотой h конуса. Она лежит на оси вращения фигуры.

Сторона AC треугольника – это радиус r конуса. Круг, который описывает этот радиус, называется основанием фигуры.

Сторона CB треугольника для конуса является его образующей, или генератрисой. Это название она получила за то, что в процессе вращения она описывает коническую поверхность.

Вершина B треугольника – это вершина конуса.

Заметим, что высота фигуры пересекает круглое основание в его центре. Это является достаточным условием, чтобы считать конус прямым.

Видео:62. Площадь поверхности конусаСкачать

Найти площадь поверхности конуса через:

образующую высотуРадиус основания (r):Образующая (l):Высота (h):

Конус – геометрическое тело, которое состоит из круга (основание конуса), точки, не лежащей в плоскости этого круга (вершина конуса), и всех точек, соединяющих вершину конуса с точками основания.

Площадь поверхности конуса формула:
, где r – радиус основания, l – образующая

Площадь поверхности конуса формула:
, где r – радиус основания, h – высота

Видео:ОТКУДА? Как найти площадь боковой поверхности конуса? Развёртка конуса | Математика с ДетекторомСкачать

Площадь куба

Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.

Формула площади куба:

Видео:Видеоурок по математике "Цилиндр"Скачать

Формула площади боковой поверхности конуса

Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:

Видео:№561. Вычислите площадь основания и высоту конуса, если разверткой его боковой поверхностиСкачать

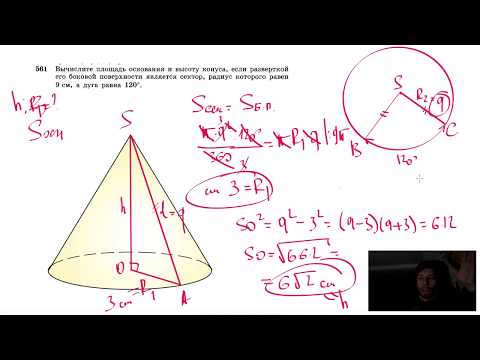
Площадь боковой поверхности конуса через его радиус и направляющую

Пусть дан конус с радиусом R и образующей L
AS=L, AO=R

Разрежем конус по образующей L и развернем его боковую поверхность.
В результате получим криволинейный треугольник ASA` , где AS=L, A`S=L.
Дуга AA` -это вытянутая окружность основания конуса с радиусом R . Следовательно, длина дуги AA` будет равна 2πR
Площадь боковой поверхности будет равна площади сектора круга с радиусом R .
Если угол α – радиальная мера угла, то:
где α=∠
Чтобы найти угол ∠ воспользуемся формулой длины дуги, которая стягивает данный угол:
Но с другой стороны:
Приравняем правые части равенств. Имеем:
Выразим α:
Подставим полученное выражение в формулу площади сектора:
Следовательно, боковая поверхность конуса равна произведению числа π на радиус конуса и его образующую.
Формула боковой поверхности конуса будет иметь следующий вид: