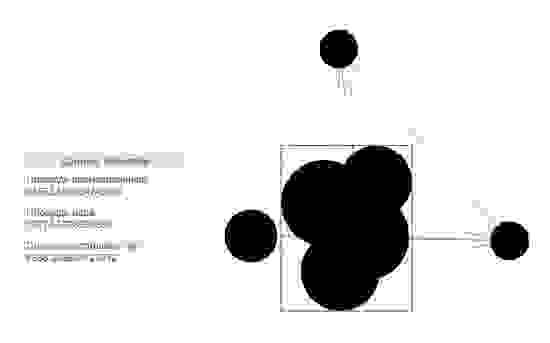
Площадь окружности методом монте карло (6 видео)

Расчет площади пересечения окружностей методом Монте-Карло

Эта статья родилась как логическое продолжение пятничного поста о методе Бутстрапа, а особенно, комментариев к нему. Не защищая метод Бутстрапа, стоит уделить внимание методам Монте-Карло. Здесь я хочу поделиться своим опытом применения Монте-Карло в одной из своих практических задач, а также обоснованием законности этого применения.

Итак, моя задача заключалась в необходимости вычисления площади фигуры, являющейся пересечением окружностей, с последующей реализацией на языке JavaScript. Площадь под графиком – это интеграл. Интегрирование методом Монте-Карло достаточно широко известно, но, как многие верно заметят, его применение требует некоторого обоснования. За подробностями прошу под кат.

Содержание

Обоснование
Реализация задачи на JavaScript
Пара гвоздей в метод Бутстрапа
Метод Монте-Карло вычисления площадей фигур и его реализация в среде Delphi
Вычисление π: моделирование методом Монте-Карло
Что такое пи?
Что такое моделирование методом Монте-Карло?
Просто: единичный квадрат и единичная окружность
2. Средние значения функций
📽️ Видео

Обоснование

Задача расчета площади пересечения двух окружностей является тривиальной геометрической задачей (координаты центров окружностей и их радиусы нам известны). Площадь пересечения двух окружностей – это сумма площадей соответствующих сегментов этих окружностей. Есть решения для расчета площади пересечения двух, трех, четырех окружностей в различных частных случаях.

А вот решения общего случая для пересечения даже трех окружностей уже далеко не так тривиальны. В процессе поиска я нашел даже исследования по расчету площади пересечения N окружностей, однако они настолько же интересны, насколько и сложны.

Здесь на сцену выходит метод Монте-Карло. Благодаря современным компьютерным мощностям этот метод позволяет провести большое количество статистических испытаний, на основе результатов которых делается обобщение.

Итак, алгоритм расчета площади любой фигуры методом Монте-Карло сводится к следующему:

Фигура вписывается в прямоугольник. Координаты сторон прямоугольника известны, значит, известна его площадь.
Псевдослучайным образом внутри прямоугольника генерируется большое количество точек. Для каждой точки определяется, попала ли точка внутрь исходной фигуры или нет.
В результате площадь исходной фигуры вычисляется исходя из обычной пропорции: отношение количества точек, попавших в фигуру, к общему количеству сгенерированных точек равно отношению площади фигуры к площади ограничивающего ее прямоугольника.

Последняя проблема, которую надо решить, заключается в том, что каким-то образом необходимо определять, попала ли точка внутрь исходной фигуры. В моем случае данная задача решается достаточно просто, поскольку моя фигура состоит из окружностей, координаты центров и радиусы которых известны.

Реализация задачи на JavaScript

Пара гвоздей в метод Бутстрапа

Если говорить именно о методе Бутстрапа, то мое личное мнение заключается в том, что случайная генерация набора данных по имеющемуся набору в общем случае не может служить для оценки закономерностей, поскольку сгенерированная информация не является достоверной. В общем, это же, только более умными (и нередко более резкими) словами, говорят и многие авторы, например, Орлов в своем учебнике по Эконометрике.

Видео:Реализация метода Монте Карло расчет площади круга программаСкачать

Метод Монте-Карло вычисления площадей фигур и его реализация в среде Delphi

В начале урока рассказываю идею метода. Ребята, сегодня мы рассмотрим интересный метод приближенного вычисления площадей фигур – метод Монте – Карло. Пусть у нас есть какая – нибудь фигура на плоскости, площадь которой ( S_fig ) нам необходимо найти. Ограничим ее другой фигурой, площадь которой ( S_total ) мы можем легко вычислить. Например, прямоугольником АСDB со сторонами, параллельными координатным осям (см. рис. 1). И пусть про любую точку прямоугольника мы можем быстро узнать, попадает эта точка внутрь фигуры, площадь которой мы ищем, или нет.

А теперь начнем опыт – будем бросать на бумагу зерна случайным образом (вообще – то это нелегко сделать, чтобы обеспечить случайность). Когда нам покажется, что зерна почти полностью покрыли бумагу, посчитаем, сколько всего зерен на прямоугольнике (пусть их число N_total ) и сколько из них на фигуре ( N_fig ). Ясно, что число зерен, попавших внутрь фигуры, пропорционально ее площади: больше площадь – больше зерен, меньше площадь – меньше зерен. Поэтому, поделив количество зерен , попавших внутрь фигуры , на количество всех зерен в прямоугольнике, мы сможем найти, какую часть площади прямоугольника занимает фигура:

Промоделируем этот опыт на ЭВМ. Предположим, нам надо найти площадь фигуры ограниченной сверху кривой Y = F(X), а снизу – осью абсцисс. Пусть Y = cos(X), а Х I [– p /2, p /2] (см. рис. 2). Ограничим нашу фигуру прямоугольником АСDB, его площадь равна p .

Из чего должен состоять алгоритм:

1. Бросание зерна – бросание случайной точки, координаты X и Y которой случайны, причем Х должна меняться от – p /2 до p /2, а Y – от 0 до 1. И в этих интервалах X и Y должны появляться с одинаковой вероятностью в любой точке этих отрезков, т.е. X и Y должны быть равномерно распределены по осям. Тут надо напомнить ребятам, как получить равномерно распределенное случайное вещественное число на интервале [А, В]:

Х = random* ( B – A) + A

2. Надо определить, куда попала точка – под кривую или выше нее. И вести подсчет N_fig. Условие попадания точки под кривую: Y ? sin (X).

3. Повторить пп.1 и 2 столько раз, чтобы получить желаемую точность результатов.

Дети без труда напишут программу по данному алгоритму (на практическом занятии). И после этого наступает момент разочарования. Сухие цифры.

Предложение учителя: давайте создадим проект в Delphi, который наглядно демонстрировал бы работу метода Монте – Карло. Разработаем интерфейс программы. Тут ребята сами предлагают несколько вариантов оформления проекта, один из которых представлен на рис. 3.

Разместим на форме следующие компоненты:

Edit – окно редактирования для ввода общего количества испытаний (бросков зерен) – N_total;

Button – кнопка для запуска работы метода Монте – Карло;

Panel – панель для вывода посчитанной площади фигуры;

(все вышеперечисленные компоненты расположены на вкладке Standart Палитры компонентов)

Image – для вывода точек, попавших в искомую область (компонент расположен на вкладке Additional Палитры компонентов).

Если необходимо, надо напомнить ребятам некоторые свойства и методы выбранных компонентов (это может быть и домашним заданием предыдущего урока, чтобы не терять время на “воспоминания”) .

Свойство Text – содержит текст, который пользователь набирает в окне Edit. Этот текст надо преобразовать в число N_total. Для этого в Delphi есть необходимая функция StrToInt:

N_total = StrToInt (Edit1.Text).

Свойство Caption – содержит текст, который выводится на панель. Чтобы вывести полученное число S_fig на панель, мы должны преобразовать его в строку S с помощью процедуры Str:

а потом вывести эту строку на панель следующим образом:

Panel1.Caption := ‘Площадь фигуры = ‘ + S

Свойства Height и Width – соответственно высота и ширина компонента;

Свойство Canvas – отводит канву (место) для рисования на компоненте Image;

FillRect(ClientRect) – закрашивает область клиента компонента Image каким – либо цветом

(по – умолчанию – белым), т.е. стирает предыдущую картинку;

MoveTo(X, Y) – перемещает перо в точку с координатами X, Y без проведения линии (координаты задаются в пикселях);

LineTo(X, Y) – проводит линию из текущей точки в точку с координатами X, Y;

Pixels[I, J] – содержит цвет точки с координатами I, J.

У кнопки (компонент Button) мы будем обрабатывать событие onClick (событие нажатие кнопки). Т.е. вышеописанный алгоритм мы программируем в процедуре Button1Click.

Тут учитель задает вопрос классу: “ Какая проблема возникает при выводе точки на экран (на компонент Image)?” Ответ: расчетные координаты очень малы (0 ? Y ? 1,меньше пикселя, -p /2 ? X ? p /2); а если взять другую кривую Y = F(X), они могут оказаться слишком большими (больше размера компонента Image). Поэтому, при выводе значений функций (графиков) на экран монитора, необходимо преобразовывать расчетные координаты в графические с учетом дискретности растровой сетки монитора, а также предусмотреть возможность автоматического масштабирования функции (графика) по осям координат. Для этого желательно создать отдельную подпрограмму.

Для полного размещения функции (графика) в расчетной области (это область компонента Image) необходимо определить X_min, X_max, Y_min, Y_max – минимальные и максимальные значения по X и по Y соответственно. X_min =А, X_max = В. Как найти Y_min, Y_max.

Коллективно обсуждается следующий алгоритм:

1. Разобьем интервал [А, В] по Х на N равных частей и определим массивы значений аргумента и функции X[i] и Y[i] = F(X[i]), где I = 1..N;
2. Определяем наибольшее Y_max и наименьшее Y_min значения функции в заданном интервале изменения аргумента;
3. Находим коэффициенты масштабирования Kx, Ky при построении графика в заданной области;
4. Т.к. коэффициенты масштабирования Kx, Ky могут отличаться, то выводимый график может искажаться. Устраняем искажения графика;
5. Преобразуем расчетные координаты точки X, Y в графические Xg, Yg. С учетом того, необходимости “переворота” оси Y, которая в координатах монитора направлена сверху вниз.

Листинг программы, реализующей данные алгоритмы представлен в конце статьи. Результат работы программы при разном количестве испытаний представлен на рис. 3, 4.

Задания для самостоятельной работы:

1. Применить метод Монте – Карло для приближенного вычисления площади фигуры, ограниченной сверху кривой Y = sin (X), при Х I [ 0, p ];
2. Применить метод Монте – Карло для приближенного вычисления числа p . Подсказка: рассмотреть круг единичного радиуса с центром в т. (1, 1). Его площадь и будет равна p .
3. Применить метод Монте – Карло для приближенного вычисления площади фигуры, ограниченной сверху кривой Y = sin (X), при Х I [ 0, 2p ];
4. Применить метод Монте – Карло для приближенного вычисления площадей фигур, представленных на рис. 5 – 7.

5. Доработать проект:

а) организавать проверку правильности ввода информации в поле Edit (чтобы вводились только целые числа);
б) разметить оси и подписать числовые значения.

На последующих уроках, на которых предполагается изучение тем “Вычисление площадей (интегралов) методом трапеций и методом прямоугольников”, можно предложить ребятам доработать проект, поместив на форму дополнительные компоненты Image, Button, Edit, Panel (для каждого численного метода – свои). В окно компонента Edit пользователь будет вводить количество разбиений интервала [А, В] по Х. Таким образом, ребята смогут сравнить и наглядно увидеть работу всех трех численных методов.

unit Monte;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ExtCtrls, Buttons;
type
TForm1 = class(TForm)
Panel1: TPanel;
BitBtn1: TBitBtn;
Edit1: TEdit;
Label1: TLabel;
Image1: TImage;

const A = -Pi/2.0; B = pi/2.0; n = 1000;

var
Form1: TForm1;
N_total:longint;
implementation

Function FUNC(x:real):real;
begin
Func:=Cos(x);
end;

Procedure Graphic( var right, down: integer;
var X_min, X_max, Y_min, Y_max, Kx, Ky: real);
type arr=array[1..n] of real;
var
X, Y: arr; dx: real;
i: integer;
begin
dx:=(B-A)/(n-1);
for i:=1 to n do begin X[i]:=A+dx*(i-1);
Y[i]:=FUNC(X[i]);
end;

X_max:=B; X_min:=A;
Y_max:=Y[1]; Y_min:=Y[1];
for i:=2 to n do begin
if Y_max Y[i] then Y_min:=Y[i];
end;

Видео:МЕТОД МОНТЕ-КАРЛО. КАК ВЫЧИСЛИТЬ ПЛОЩАДЬ КЛЕНОВОГО ЛИСТА?Скачать

Вычисление π: моделирование методом Монте-Карло

Mar 21, 2020 · 6 min read

Каждый год 14 марта любители математики отмечают День числа пи! Есть много способов вычислить это легендарное число π, которое примерно равно 3,14159…

Обсудим все эти методы и рассмотрим три способа вычисления π с использованием моделирования методом Монте-Карло!

Видео:Вычисление числа ПИ методом Монте-КарлоСкачать

Что такое пи?

Пи — это число, которое выражает отношение длины окружности к её диаметру, приблизительно равное 3,14159…

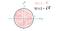
Нарисуем единичную окружность (т.е. окружность с радиусом 1).

Как известно, площадь круга (окружности) равна:

Для единичной окружности, где r = 1, площадь равна π, а периметр равен 2π. То есть π — это есть одновременно и площадь единичной окружности, и её полупериметр.

Суще с твует великое множество способов вычисления числа π. Помимо детерминистских методов, то есть методов без использования элемента случайности, есть ещё вероятностные методы. Последние объединяются под одним общим названием «моделирование методом Монте-Карло». Прежде чем уходить с головой в математику, разберёмся с тем, что представляет собой моделирование методом Монте-Карло.

Видео:Вычисление числа Пи методом Монте-КарлоСкачать

Что такое моделирование методом Монте-Карло?

Моделирование методом Монте-Карло основано на экспериментах или вычислительных алгоритмах, использующих выборку случайных величин. Моделирование случайных величин в таких экспериментах имеет повторяющийся характер, то есть модель многократно перерасчитывается для получения данных и нахождения искомых параметров, причём последние могут быть определены и детерминированно. Например, число π является детерминированным, т.е. не зависящим от элемента случайности или вероятности.

Моделирование методом Монте-Карло применяется, когда детерминированные вычисления сопряжены со слишком большими вычислительными затратами или неосуществимы. Ну… или если экспериментатор слишком ленив для точных вычислений.

Бывает и так, что в моделировании методом Монте-Карло нет никакой необходимости, а просто хочется продемонстрировать всю красоту математики и теории вероятности.

Мне больше нравится третья причина, так что давайте скорее начнём вычислять наше любимое число π! У меня для вас три способа вычисления пи: простой, сложный и неожиданный.

Видео:Что такое метод Монте-Карло (простым языком)Скачать

Просто: единичный квадрат и единичная окружность

Рисуем единичный квадрат — такой же, как на рисунке ниже — и наносим, равномерно распределяя по всему квадрату, n точек. Пусть внутри круга с радиусом 1 оказалось m точек этого квадрата. Напомним, что квадрант — это четверть окружности.

Дробь m/n определяет отношение площадей квадранта и квадрата, равное 1/4 π.

Давайте разберёмся, откуда взялись такие цифры.

Площадь квадрата, в котором оказался наш квадрант с точками, определяется так:

Площадь квадранта определяется так:

Используя соотношение этих площадей, находим π:

Теперь это отношение площадей умножаем на четыре и получаем π. Например, если из 100 точек 76 оказались внутри четверти окружности, то π будет приблизительно равно:

Что ж, неплохо. Теперь нанесём 1 000 точек, 780 из которых внутри четверти окружности, тогда π будет равно:

Ещё ближе к истине! Результат будет тем точнее, чем больше точек наносится, пока мы наконец не подберёмся благодаря закону больших чисел к реальному значению π. Вот он наш самый первый и, пожалуй, самый простой — к тому же самый очевидный — метод вычисления π с использованием в расчётах элемента случайности!

Этот способ отлично подходит для общего понимания моделирования методом Монте-Карло. Его без труда могут освоить даже младшие школьники. Обратимся теперь к менее очевидному и математически более сложному способу.

Видео:12.3 Метод Монте Карло 1. "Поколение Python": курс для продвинутых. Курс StepikСкачать

2. Средние значения функций

Этот способ очень часто используют при вычислении интегралов, когда вычислительные затраты, связанные с получением точных результатов, слишком велики. Среднее значение непрерывной функции f(x) определяется следующим образом: