Пересекающиеся параллельные и скрещивающиеся прямые линии

Видеоурок: Параллельные прямые, перпендикулярные к плоскости

Лекция: Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых

Пересекающиеся прямые

Если на плоскости имеются несколько прямых, то они либо рано или поздно пересекутся произвольно, либо под прямым углом, или же будут параллельными. Давайте же разберемся с каждым случаем.

Пересекающимися можно назвать те прямые, у которых будет хотя бы одна точка пересечения.

Вы спросите, почему хотя бы одна, не может же прямая пересечь другую прямую две или три раза. Вы правы! Но прямые могут полностью совпасть друг с другом. В таком случае общих точек будет бесконечное множество.

Параллельность

Параллельными можно назвать те прямые, которые никогда не пересекутся, даже на бесконечности.

Иными словами, параллельные – это те, у которых нет ни одной общей точки. Обратите внимание на то, что данное определение справедливо только в том случае, если прямые находятся в одной плоскости, если же они не имеют общих точек, находясь в разных плоскостях, то они считаются скрещивающимися.

Примеры параллельных прямых в жизни: два противоположных края экрана монитора, линии в тетрадях, а также многие другие части вещей, имеющих квадратную, прямоугольную и другие формы.

Когда хотят показать на письме, что одна прямая параллельная второй, то используют следующее обозначение a||b. Данная запись говорит, что прямая а параллельна прямой b.

При изучении данной темы важно понять еще одно утверждение: через некоторую точку на плоскости, которая не принадлежит данной прямой, можно провести единственную параллельную прямую. Но обратите внимание, снова поправка – на плоскости. Если рассматривать трехмерное пространство, то можно провести бесконечное множество прямых, которые не будут пересекаться, но будут скрещивающимися.

Утверждение, которое было описано выше, называется аксиомой о параллельности прямых.

Перпендикулярность

Прямые можно назвать только в том случае перпендикулярными, если они пересекаются под углом, равным 90 градусов.

В пространстве через некоторую точку на прямой можно провести бесконечное множество перпендикулярных прямых. Однако, если речь идет о плоскости, то через одну точку на прямой можно провести единственную перпендикулярную прямую.

Скрещенные прямые. Секущая

У любых скрещивающихся прямых есть вертикальные углы и смежные.

Если у углов, которые образованы двумя скрещивающимися прямыми, одна сторона общая, то они называются смежными:

Смежные углы в сумме дают 180 градусов.

Если же углы, образованные двумя скрещивающимися прямыми, не имеют общей стороны, то они называются вертикальными:

Вертикальные углы всегда равны.

Если же некоторая прямая пересекает две других прямых, то она называется секущей.

Частным случаем является секущая двух параллельных прямых:

Взаимное расположение двух прямых в пространстве.
Признак скрещивающихся прямых.
Угол между скрещивающимися прямыми

Взаимное расположение двух прямых в пространстве

Признак скрещивающихся прямых

Угол между скрещивающимися прямыми

Взаимное расположение двух прямых в пространстве

Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.

Фигура	Рисунок	Определение
Две пересекающиеся прямые		Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.
Две параллельные прямые		Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек
Две скрещивающиеся прямые		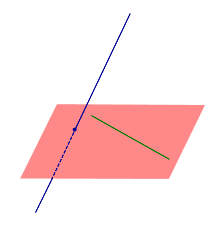Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

Две пересекающиеся прямые

Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.

Две параллельные прямые

Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек

Две скрещивающиеся прямые

Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.

Фигура	Рисунок	Тип утверждения и формулировка
Две различные точки		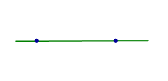Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия.
Прямая линия и точка, не лежащая на этой прямой		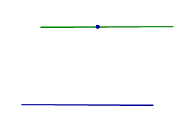Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.
Две пересекающиеся прямые		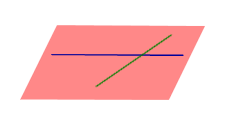Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.
Две параллельные прямые		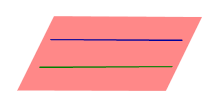Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две различные точки

Аксиома о прямой линии, заданной двумя точками
Через две различные точки проходит одна и только одна прямая линия.

Прямая линия и точка, не лежащая на этой прямой

Аксиома о параллельных прямых
Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.

Две пересекающиеся прямые

Теорема о плоскости, определяемой двумя пересекающимися прямыми
Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две параллельные прямые

Теорема о плоскости, определяемой двумя параллельными прямыми
Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Признак скрещивающихся прямых

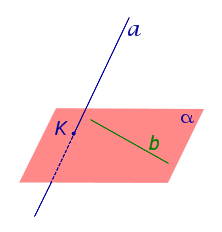
Признак скрещивающихся прямых . Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).

Доказательство . Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».

Для этого предположим, что прямая a , пересекающая плоскость в точке K , и прямая b , лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α . Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K , не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости . Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость , а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.

Угол между скрещивающимися прямыми

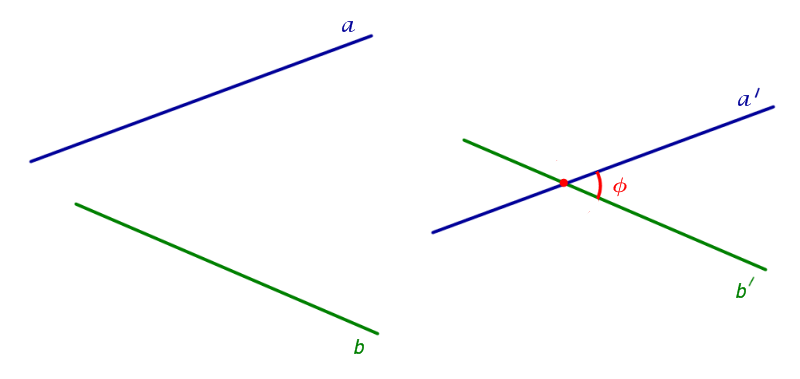
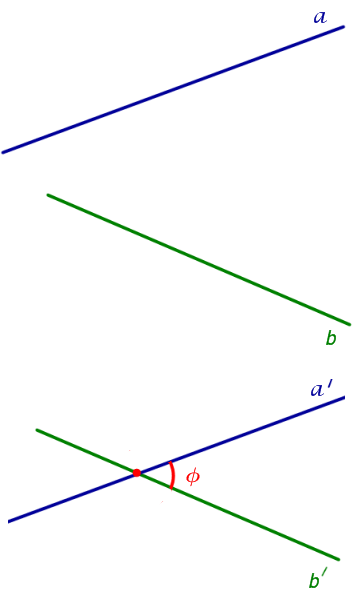
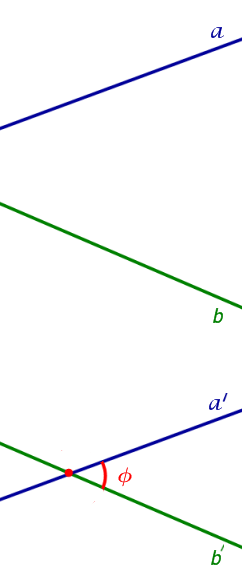
На рисунке 2 изображены скрещивающиеся прямые a и b . Прямая a’ параллельна прямой a , прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b .

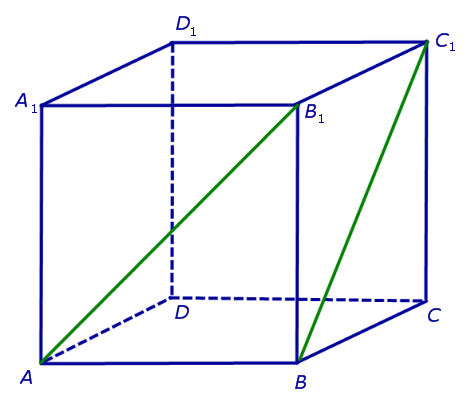
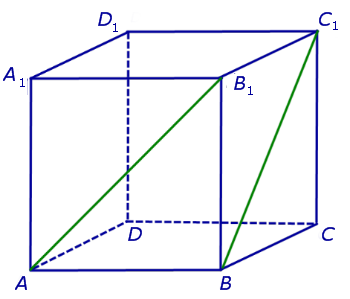
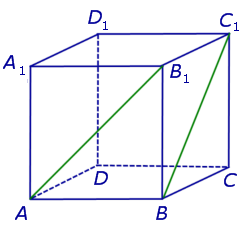
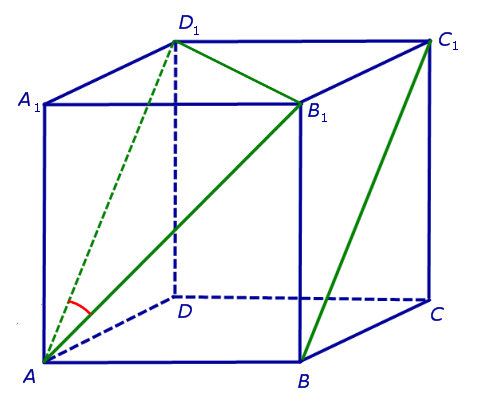
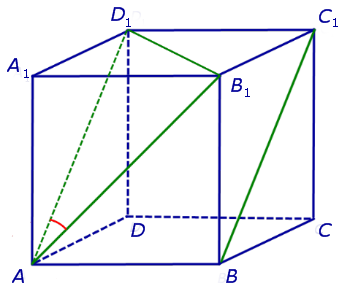
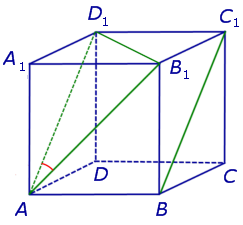
Для того, чтобы найти угол между прямыми AB₁ и BC₁ , проведем в кубе диагональ боковой грани AD₁ и диагональ верхнего основания D₁B₁ (рис. 4).

Замечание . Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Свойства скрещивающихся прямых» и «Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости».

Параллельные, пересекающиеся и скрещивающиеся прямые

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ ЛИНИЙ

4.1 Параллельные, пересекающиеся и скрещивающиеся прямые

Две прямые в пространстве, быть параллельными (c || d), пересекаться (e ∩ g), скрещиваться (k./ l ) а также могут совпадать (a ≡b).

Если две прямые совпадают, то совпадают их одноименные проекции на комплексном чертеже

Если две прямые параллельны, то на комплексном чертеже их одноименные проекции параллельны.

Рисунок 27 Эпюр параллельных прямых

Если две прямые пересекаются в некоторой точке С, то проекции этой точки должны принадлежать одноименным проекциям прямых, т. е. точки пересечения одноименных проекций пересекающихся прямых должны лежать на одной линии связи: d ∩ e = С → d’ ∩ e’ = С’; d»∩ e» = С».

Рисунок 28 Эпюр пересекающихся прямых

Две скрещивающиеся прямые не имеют общей точки. Поэтому их одноименные проекции пересекаются в точках, не лежащих на одной линии связи: f ∩ g →f’ ∩ g’ = K’ (L’); f» ∩ g» = M’ ‘ (N»).

Здесь K и L − горизонтально — конкурирующие, а M и N − фронтально конкурирующие точки.

Рисунок 29 Эпюр скрещивающихся прямых

Взаимно — перпендикулярные прямые

Пусть задана фронталь f. Требуется из точки A опустить на фронталь перпендикуляр n.( рисунок 30).

На основании теоремы о проецировании прямого угла прямой угол проецируется без искажения на плоскость проекций, если одна из его сторон − линия уровня. Следовательно, прямой угол между f и n проецируется на П2 в натуральную величину: n» ┴ f», так как n ┴ f и f || П2.

Точка 1 − основание перпендикуляра. Горизонтальная проекция перпендикуляра n’ определяется положением точек 1′ и A’.

Аналогично строится перпендикуляр к горизонтали h.

Рисунок 30 Построение перпендикуляра к фронтали

4.3 Определение натуральной величины отрезка

Длину (натуральную величину) отрезка общего положения можно определить на основании ортогонального проецирования отрезка на

плоскость, как длину гипотенузы AB прямоугольного треугольника один катет которого, например A’B’ является проекцией отрезка, а другой равен превышению одного конца отрезка над другим Д z.

Пространственная модель отрезка, который проецируется на плоскости проекций

Таким образом, на горизонтальной проекции комплексного чертежа отрезка можно построить прямоугольный треугольник, взяв вторым катетом Д z. Гипотенуза этого треугольника будет натуральной величиной (НВ) отрезка AB, а угол б определит угол его наклона к горизонтальной плоскости проекций П1.

Определение натуральной величины отрезка на эпюре

Аналогичное построение можно сделать на фронтальной проекции отрезка, взяв в качестве второго катета разность глубин его концов Д 1 с плоскости П1. Здесь в − угол между AB и плоскостью П2

🔍 Видео