а) прямая лежит в плоскости данного треугольника, если она пересекает две его стороны во внутренних точках.
Решение:
Ответ: утверждение истинно.
б) прямая лежит в плоскости данного треугольника, если она пересекает две его стороны.
Решение:
Ответ: утверждение не истинно.
Видео:№52. Две стороны треугольника параллельны плоскости α. Докажите, что и третья сторонаСкачать

Прямая а пересекает две стороны треугольника и параллельна третьей его стороне. Докажите, что прямая а рассекает стороны этого
Видео:№10. Верно ли, что прямая лежит в плоскости данного треугольника, если онаСкачать

Ваш ответ
Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Похожие вопросы
- Все категории
- экономические 43,279
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,962
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:№241. Прямая, параллельная основанию равнобедренного треугольника ABC, пересекает боковые стороны АВСкачать

Теорема Менелая
Видео:Уравнения стороны треугольника и медианыСкачать

Определение Теоремы Менелая
Теорема Менелая показывает соотношение сторон треугольника, которое получается, когда прямая пересекает две стороны треугольника и продолжение третьей.
С помощью этой теоремы можно получить соотношения сторон треугольника и доказать коллинеарность точек, которые находятся на данном треугольнике (на двух сторонах и продолжении третьей).
Коллинеарными точками называются три или более точки, которые лежат на одной прямой.
Теорема Менелая гласит:
BD/DC * CE/EA * AF/FB = 1
Шаг 1. Есть треугольник ABC. Прямая пересекает две стороны треугольника, таким образом, что она не проходит через вершину треугольника (на нашем рисунке это розовая линия). Таким образом получились две точки пересечения прямой с двумя сторонами треугольника (точки E и D). Третью сторону (AB) нужно продолжить до пересечения (получилась точка пересечения F).
Шаг 2. Берём точку треугольника и начинаем двигаться в другую точку треугольника, проходя через точку пересечения (потом делим один на другой): BD/DC
Обратите внимание, что в такой записи видно точку пересечения посередине («DD»), а B и C (сторона треугольника, по которой мы идём) по бокам. Т. е. мы идём из B к C через D. Можно написать точки стороны, по которой мы идём («BC»), оставив небольшое место между ними, и потом вставить между ними дважды точку пересечения со знаком дроби («D/D»).
В записи дробью точка, через которую мы идём повторяется наискосок.
На рисунке обозначить карандашом стрелочками по какой стороне мы уже прошлись и в какую сторону, и не запутаетесь.
Шаг 3. Идём дальше по треугольнику, делаем сторону CA — это будто прийти от C к A через E, что получается CE/EA.
Эти две стороны умножаются и в тетради, записывается всё вместе:
Шаг 4. Теперь делаем сторону AB через точку F — из A мы сначала пойдём в F, а потом уже вернёмся к B, получится так: AF/FB.
Шаг 5. Перемножаем всё вместе:
BD/DC * CE/EA * AF/FB
Теорема Менелая гласит:
BD/DC * CE/EA * AF/FB = 1
Видео:Задание №10 — ГДЗ по геометрии 10 класс (Атанасян Л.С.)Скачать

Доказательство теоремы Менелая
Есть много способов доказать эту теорему, этот называется «Доказательство с подобными треугольниками»:
Проводим линию, которая параллельна QN через точку A, чтобы пересечь сторону BC в точке M.
Видео:№470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведенная кСкачать
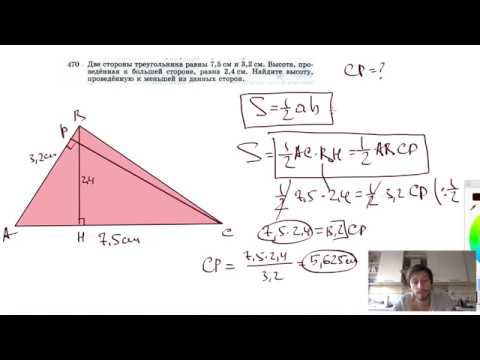
Теорема Менелая пример (задача с решением)
Есть треугольник АВС. На стороне ВС стоит точка L, такая, что LC = 3BL. За точку А идёт продолжение стороны АС, где взята точка М, таким образом, что МА = АС. Прямая ML пересекает АВ в точке F.
Найдите соотношение BF/FA:
1. Мы знаем, что МА = АС, LC = 3BL.
2. Прямая ML пересекает две стороны треугольника АВС и является продолжением третьей, значит по теореме Менелая:
Видео:Найдите сторону треугольника на рисункеСкачать

Что такое теорема Чевы?
Пусть на сторонах треугольника ABC отмечены точки A’, B’ и C’. Отрезки AA’, BB’ и CC’ пересекаются в одной точке тогда и только тогда, когда справедливо равенство:
Заметьте, что логика та же самая: идём из А в С через В’ и т. д.
Чевиана — это отрезок, который соединяет вершину треугольника с точкой на противоположной стороне.
💡 Видео
РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Чему равна сторона треугольника, у которого медианы пересекаются под прямым угломСкачать

Найдите третью сторону треугольникаСкачать

Нахождение стороны прямоугольного треугольникаСкачать

СЕРЬЁЗНО готовимся к ОГЭ 2023! / Полный прогон задания 15 на ОГЭ по математикеСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

✓ Самая сложная задача в ОГЭ-2020 | Задание 26. Математика | Геометрия | Борис ТрушинСкачать

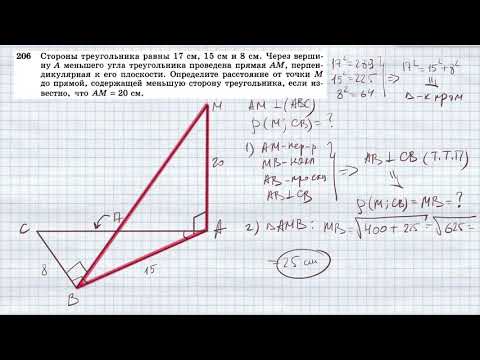
№206. Стороны треугольника равны 17 см, 15 см и 8 см. Через вершину A меньшего угла треугольника проСкачать
Как я использую дюймы в пэчворке и не пересчитываюСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать











