Пересечение высот треугольника теорема эйлера

Рассмотрим произвольный треугольник. Теорема Эйлера об окружности девяти точек гласит: основания высот, середины сторон и середины отрезков, соединяющих точку пересечения с вершинами треугольника, лежат на одной окружности девяти точек.

Непрерывно изменяя исходный треугольник, получаем мультфильм.

При гомотетии с центром в ортоцентре треугольника и описанная окружность треугольника переходит в окружность девяти точек.

При этой гомотетии центр описанной окружности переходит в центр окружности девяти точек. Следовательно, центр окружности девяти середина отрезка, соединяющего ортоцентр треугольника с центром его описанной окружности.

При гомотетии с центром в точке пересечения медиан и вершины треугольника переходят в середины противоположных сторон. Поэтому при этой гомотетии высоты переходят в серединные перпендикуляры, а в центр описанной окружности. Это значит, что центр тяжести треугольника (точка пересечения его медиан) лежит на отрезке, соединяющем ортоцентр и центр описанной окружности, и расположена вдвое ближе к центру описанной окружности, чем к ортоцентру.

Таким образом, центр описанной окружности, центр тяжести, центр окружности девяти точек и ортоцентр лежат на одной прямой Эйлера.

Вот как меняется прямая Эйлера при движении вершин треугольника.

А вот так выглядят прямая Эйлера и окружность девяти точек, изображённые на одном рисунке.

Видео:Геометрия 8 класс (Урок№31 - Теорема о пересечении высот треугольника.)Скачать

Прямая Эйлера

Деление отрезка в данном отношении.

Теорема о пересечении медиан треугольника в одной точке.

Теорема о высотах произвольного треугольника.

Прямая Эйлера тетраэдра.

Использованные источники информации.

Свойства треугольника были хорошо изучены еще древними греками.

В знаменитых “Началах” Евклида доказывается, что центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к его сторонам.

Архимед, определяя положение центра тяжести однородной треугольной пластинки, установил, что он лежит на каждой из трех медиан. Точку пересечения медиан треугольника называют центром тяжести или центроидом треугольника.

Позднее было доказано, что три высоты треугольника также пересекаются в одной точке, которая называется его ортоцентром.

Закономерность в расположении этих трех замечательных точек треугольника – центра O описанной окружности, центроида G , ортоцентра H – впервые обнаружил знаменитый математик Леонард Эйлер (1707-1783).

Рассмотрим сначала один частный случай: прямоугольный треугольник ABC (рис.1). Середина O гипотенузы AB является центром описанной около него окружности. Центроид G делит медиану CO в отношении 1:2, считая от вершины C. Катеты AC и BC являются высотами треугольника, поэтому вершина C прямого угла совпадает с ортоцентром H треугольника. Таким образом, точки O,G,H лежат на одной прямой, причем OH=3OG. Пользуясь методом координат, Эйлер доказал, что такая же связь существует между тремя указанными точками любого треугольника. Мы докажем этот факт с помощью векторов.

Деление отрезка в данном отношении.

Пусть A,B,O – данные точки плоскости, и известно, что

точка G делит отрезок AB в отношении k: ——- = k (рис.2).

Выразим вектор OG через векторы OA и OB. Для этого подставим в равенство AG=k * GB выражения всех векторов через OG, OA и OB: OG-OA=k(OB-OG). Решая это уравнение относительно OG , получим:

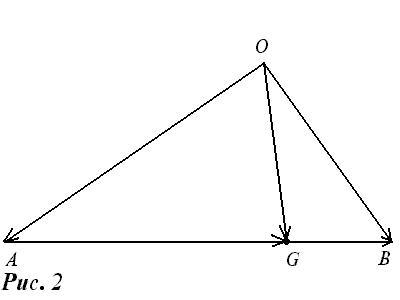
Например, если G – середина отрезка AB , то k=1 и OG= — (OA+OB).

Теорема о пересечении медиан треугольника в одной точке.

Здесь мы попутно получим одно векторное равенство, которое понадобится нам в дальнейшем.

Теорема 1. Медианы треугольника АВС пересекаются в одной точке G и делятся ею в отношении 2:1, считая от вершины, причем

где P – любая точка плоскости или пространства.

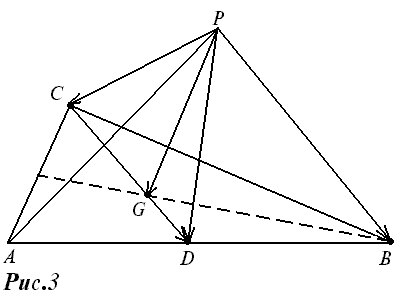
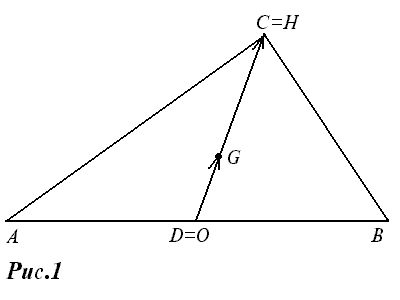
Доказательство. Возьмем на медиане CD треугольника ABC точку G, определяемую соотношением |CG|:|GD|=2:1 (рис. 3).

Согласно формуле (1),

PG = — (PA + PB + PC).

Вычисляя вектор PG’ с концом в точке G’, делящей любую из двух других медиан треугольника в отношении 2:1 (считая от вершины), мы получим то же самое выражение:

Поэтому PG’=PG, и точка G’ совпадает с точкой G. Следовательно, все три медианы треугольника пересекаются в одной точке G, определяемой соотношением (2).

Теорема о высотах произвольного треугольника.

Теорема 2. Высоты треугольника АВС пересекаются в одной точке Н, причем

OH= OA + OB + OC, (3)

где О – центр окружности описанной около треугольника.

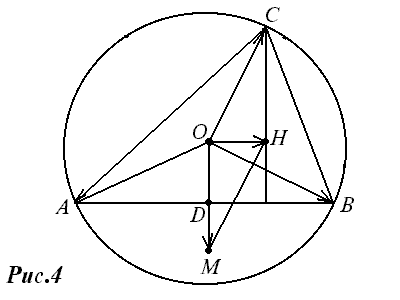
Доказательство. Пусть АВС – треугольник, отличный от прямоугольного (рис.4).

Найдем сумму векторов OA и OB. Для этого построим точку M, симметричную О относительно стороны AB, тогда OM = OA + OB. Затем построим точку Н, для которой

OH = OM + OC = OA + OB +OC,

и докажем, что точка H и есть ортоцентр треугольника АВС.

Действительно, по построению прямые CH и OM параллельны, OM – серединный перпендикуляр к отрезку АВ, следовательно, прямая СН также перпендикулярна к прямой AB, и точка H лежит на высоте треугольника ABC, проведенной из вершины C.

Если повторить построение, начиная с векторов OA и OC, то получится та же точка H, но те же рассуждения показывают, что теперь точка H лежит на высоте треугольника, проведенной из вершины B. Аналогично получим, что точка H лежит на высоте, проведенной из вершины A. Следовательно, высоты треугольника ABC пересекаются в точке H, определяемой соотношением (3).

Легко проверить, что теорема 2 справедлива и для прямоугольного треугольника.

Из доказанных теорем 1 и 2 вытекает интересующее нас свойство замечательных точек треугольника.

Теорема 3. Центр О описанной окружности, центроид G и ортоцентр H любого треугольника лежат на одной прямой, причем точка G лежит между точками О и Н и OG:GH = 1:2.

Доказательство. По теореме 1

3OG = OA + OB + OC.

Сравнивая это равенство с равенством (3), получим

Следовательно, векторы OH и OG, имеющие общее начало O, расположены на одной прямой и | OG| : |GH| = 1 : 2.

Прямая, на которой лежат точки O, G и H, называется прямой Эйлера.

В стереометрии простейший многогранник – тетраэдр играет ту же роль, что и треугольник в планиметрии. Свойства треугольника и тетраэдра во многом схожи. Попробуем распространить свойство замечательных точек треугольника на тетраэдр.

Сфера, описанная около тетраэдра.

Известно, что около всякого тетраэдра можно описать сферу, её центр O лежит на перпендикулярах к граням тетраэдра, восстановленных в центрах окружностей, описанных около граней.

Отрезок, соединяющий вершину тетраэдра с центроидом противоположной грани, называется медианой тетраэдра. Свойства медиан тетраэдра аналогичны свойствам медиан треугольника.

Теорема 4. Четыре медианы тетраэдра ABCD пересекаются в одной точке G, которая делит каждую из них в отношении 3:1, считая от вершины тетраэдра, причем

4PG = PA + PB +PC +PD, (4)

где P – любая точка пространства.

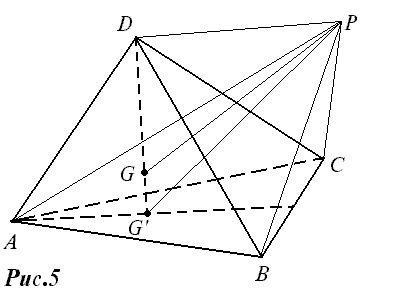
Доказательство. Возьмем на медиане DG’ тетраэдра ABCD точку G, определяемую соотношением DG : GG’ = 3 : 1 (рис 5). Согласно формуле (1),

Учитывая, что центроид G’ треугольника ABC удовлетворяет соотношению 3PG = PA + PB + PC, получим

PG = — (PA + PB + PC + PD).

Вычисляя вектор PG’’ с концом в точке G’’ , делящей любую из трех других медиан тетраэдра в отношении 3 : 1 (считая от вершины), получим то же самое выражение. А это означает, что все четыре медианы тетраэдра пересекаются в одной точке G, удовлетворяющей соотношению (4). Точка G, называется

центром тяжести (или центроидом) тетраэдра.

Высоты треугольника всегда пересекаются в одной точке. По аналогии можно предположить, что высоты любого тетраэдра также пересекаются в одной точке. Однако это не так.

Для примера рассмотрим тетраэдр ABCD с прямым двугранным углом при ребре AB, в котором AC = BC, но AD = BD (рис. 6). Высоты CE и DF тетраэдра лежат соответственно в гранях ABC и ABD, но точка E – середина AB, а F – нет. Если бы длины ребер DA и DB были равны, то основания E и F совпадали бы, но две другие высоты тетраэдра не могут проходить через точку E.

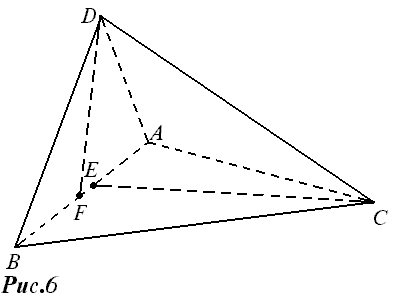
Таким образом, даже две высоты тетраэдра могут не иметь общей точки.

Тем не менее существуют и тетраэдры, все четыре высоты которых пересекаются в одной точке. Таким будет, например, тетраэдр ABCD с прямыми плоскими углами при вершине D. Ребра DA, DB и DC являются его высотами, а вершина D – ортоцентром (точкой пересечения всех четырех высот).

Попробуем найти все тетраэдры, у которых высоты пересекаются в одной точке.

Пусть высоты тетраэдра ABCD, проведенные из вершин C и D , пересекаются в точке H

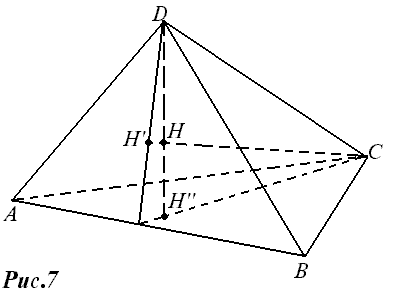
(рис. 7). Тогда CH’__AB и DH’’__AB, т.е. прямая AB перпендикулярна к двум пересекающимся прямым лежащим в плоскости CDH, следовательно, AB__BC. Аналогично доказывается, что если две другие высоты тетраэдра ABCD проходят через ту же точку H, то AC__BD и AD__BC. Итак, если все высоты тетраэдра пересекаются в одной точке, то противоположные ребра тетраэдра взаимно перпендикулярны. Такой тетраэдр называется ортоцентрическим.

Теорема 5. Четыре высоты ортоцентрического тетраэдра ABCD пересекается в одной точке H, причем если O – центр сферы, описанной около тетраэдра, то

OH = —(OA + OB + OC + OD). (5)

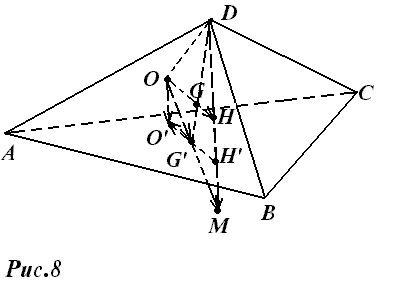
Доказательство. Пусть ABCD – ортоцентрический тетраэдр, DG’ – его медиана, DH’ – его высота (рис.8). Тогда G’ центроид, а H’- ортоцентр треугольника ABC, причем точки O’ (центр окружности, описанной около треугольника ABC ), G’ и H’ лежат на одной прямой. Заметим, что центр O сферы, описанной около тетраэдра ABCD, лежит на перпендикуляре к плоскости треугольника ABC, восстановленном в точке O’.

Будем доказывать теорему тем же способом, что и теорему 2 для треугольника: строить разными способами точку H, удовлетворяющую соотношению (5).

Вначале сложим векторы OA, OB и OC:

OG’ = — (OA + OB + OC),

или G’M = 2OG’ . Точки O’,G’,H’, лежат на прямой Эйлера треугольника ABC, причем H’G’ = 2G’O’. Следовательно,

Отсюда вытекает, что прямые H’M и OO’ параллельны, а так как прямая OO’ перпендикулярна к плоскости ABC, то и прямая H’M перпендикулярна к этой плоскости. Следовательно, точка M’ лежит на прямой DH’ (если точки O и O’ совпадают, то точки M и H’ тоже совпадают).

Из левого равенства следует, что точка H является серединой отрезка DM, т.е. точка H лежит на DH’ тетраэдра.

Аналогично строится точка N: ON=OA+OB+OD и та же точка H: OH= —(ON+OC) и доказывается, что точка H лежит на высоте тетраэдра, проведенной из вершины C, и т.д.

Следовательно, высоты ортоцентрического тетраэдра пересекаются в одной точке H, определяемой соотношением (5).

Прямая Эйлера тетраэдра.

Теорема 6. Центр О описанной сферы, центроид G и ортоцентр Н ортоцентрического тетраэдра ABCD лежат на одной прямой, причем точки О и Н симметричны относительно точки G.

Доказательство. По формулам (4) и (5)

OH= — (OA + OB + OC +OD),

OG= — (OA + OB + OC + OD),

откуда OH=2OG. Полученное равенство означает, что точки O, G, H лежат на одной прямой, причем точки О и Н симметричны относительно точки G.

Прямую, на которой лежат точки O, G, H, можно назвать прямой Эйлера ортоцентрического тетраэдра.

В данном реферате собран материал необходимый для выявления прямой Эйлера и прямой Эйлера тетраэдра .

Использованные источники информации:

“Прямая Эйлера” (Э. Готман).

Международная информационная сеть Internet (URL: ).

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Видео:76. Теорема о пересечении высот треугольникаСкачать

Прямая Эйлера

Прямая Эйлера — это такая прямая, на которой лежат следующие точки:

• центроид треугольника (точка пересечения его медиан);
• ортоцентр треугольника (точка пересечения его высот);
• центр описанной около треугольника окружности (точка пересечения серединных перпендикуляров, проведённых к сторонам этого треугольника).

Видео:8 класс, 37 урок, Теорема о пересечении высот треугольникаСкачать

Доказательство существования прямой Эйлера

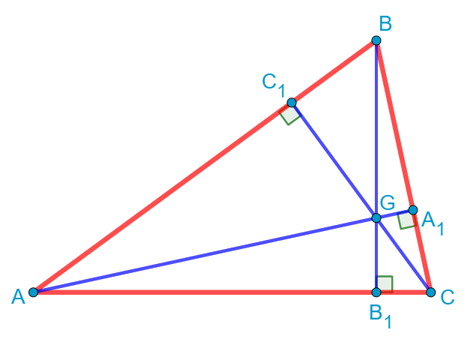
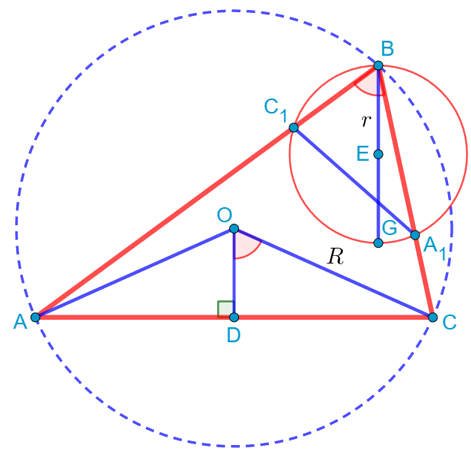
Нарисуем треугольник общего вида. Единственное, пусть он будет остроугольным. Хотя на самом деле все дальнейшие рассуждения с небольшими косметическими поправками будут справедливы и для тупоугольного треугольника. Проведём в этом треугольнике все высоты. Как известно, в треугольнике либо сами высоты, либо их продолжения пересекаются в одной точке. Назовём её точкой G. По-другому эта точка называется «ортоцентром»:

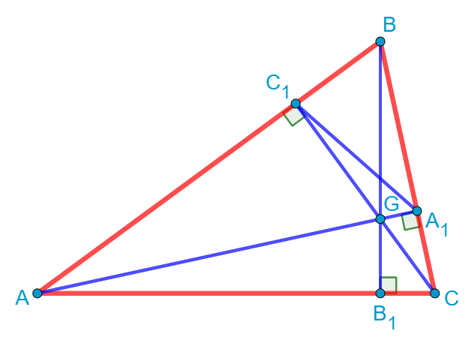
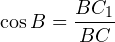
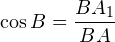
Соединим теперь основания высот A₁ и C₁ отрезком. И докажем, что треугольник C₁BA₁ подобен треугольнику ABC. Ну, действительно. У них есть общий угол B. Кроме того, если рассмотреть прямоугольный треугольник CC₁B, то косинус угла B в нём равен отношению прилежащего катета BC₁ к гипотенузе BC: . С другой стороны, из прямоугольного треугольника ABA₁ мы получаем, что косинус того же самого угла B равен отношению прилежащего катета BA₁ к гипотенузе BA: :

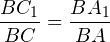
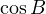
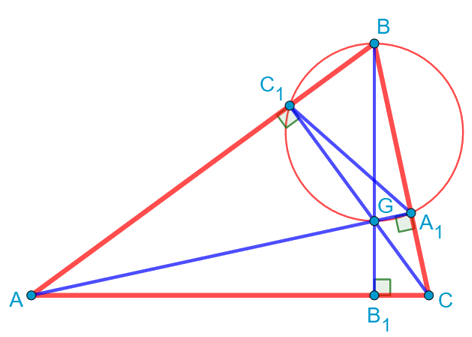
Ну и теперь мы видим, что общий угол B образован в наших треугольниках пропорциональными сторонами: . Значит, треугольники C₁BA₁ и ABC подобны. Причём их коэффициент подобия равен .

Обратим теперь внимание на то, что 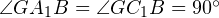. Это означает, что сумма противоположных углов четырёхугольника GC₁BA₁ равна 180 градусам. Значит, вокруг него можно описать окружность:

При этом отрезок BG будет являться диаметром этой окружности, поскольку на него опирается вписанный угол BA₁G, который равен 90 градусов.

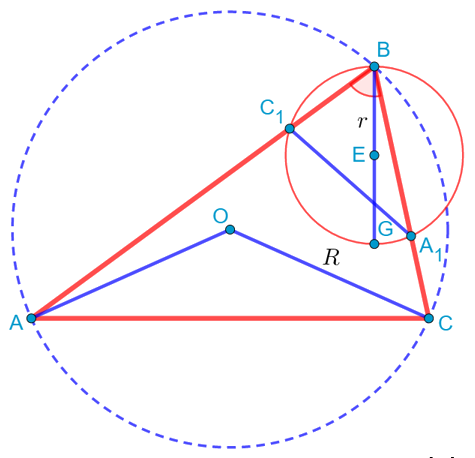
Проведём теперь серединные перпендикуляры к сторонам AB и AC. Они пересекутся в точке O, которая, как хорошо известно, является центром описанной около треугольника ABC окружности. То есть треугольник AOC будет равнобедренным, причём его боковые стороны по длине будут равны радиусу описанной окружности:

То есть мы получили, что вокруг подобных треугольников BC₁A₁ и ABC описаны окружности. Но коэффициент их подобия равен косинусу угла B. Но в подобных треугольниках одинаковым образом относятся все элементы, в том числе и радиусы описанных окружностей, поэтому .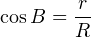

Проведём теперь высоту OD в треугольнике AOC. Обратим внимание, что угол B является вписанным и опирается на дугу AC. Но на эту же дугу опирается и центральный угол AOC, который поэтому должен быть вдвое больше угла B. Но высота OD делит этот угол ровно пополам, так как она является одновременно и биссектрисой, проведённой к основанию равнобедренного треугольника. Значит, ∠B = ∠DOC:

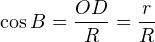
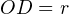
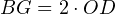
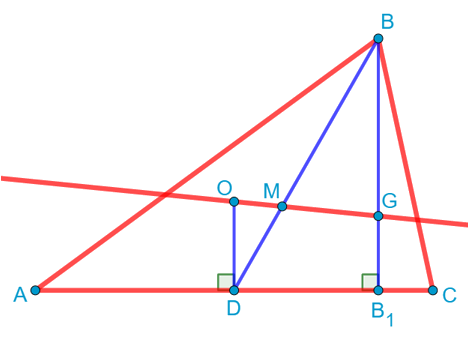
Но тогда косинус угла B мы можем расписать, используя треугольник DOC. В нём этот косинус равен отношению прилежащего катета OD к гипотенузе OC, которая равна радиусу описанной окружности R. И этот же косинус, как мы выяснили, равен отношению r к R: . Из последнего равенства получаем, что или иначе .

Проведём теперь отрезок BD, который будет являться медианой. Проведём также прямую через точки O и G. То есть через эти две точки проходит прямая, что, конечно, не удивительно, ведь мы знаем, что через две точки можно провести прямую, притом только одну. Эта прямая пересекает медиану BD в некоторой точке M:

Как вы думаете, что это за точка? Уже догадались? А может быть уже знали и раньше? Если нет, то настало время удивляться! Посмотрите на треугольник OMD. Он подобен треугольнику MGB по двум углам: вертикальным и накрест лежащим при параллельных прямых. И мы даже знаем коэффициент подобия этих треугольников. Он равен 1:2. А значит, все стороны этих треугольников относятся как 1:2, в том числе и стороны DM и MB.

И что же у нас получилось? А получилось то, что точка M делит медиану BD в отношении 2:1, считая от вершины. А значит, точка M – это точка пересечения медиан треугольника или, как её по-другому называют, цетроид треугольника.

Таким образом мы доказали, что ортоцентр треугольника, центр описанной около него окружности и центроид этого треугольника лежат на одной прямой. Эта прямая и называется прямой Эйлера!

Видео:Окружность девяти точек, Эйлера, Фейербаха, Теркема...Скачать

Анимация прямой Эйлера

Факт существования прямой Эйлера насколько удивителен, что даже не всегда укладывается в голове. Специально для вас я подготовил поясняющую анимацию. Посмотрите её в видео на моём Youtube-канале.

Вне зависимости от типа треугольника, как угодно можно над ним издеваться, но эти три точки всегда будут лежать на одной прямой. Возможны, правда, случаи, когда эти точки совпадают. Например, для правильного треугольника все они сливаются в одну точку. Но если мы имеем дело не с этим тривиальным случаем, то все эти точки лежат на одной прямой. Прямой Эйлера.

И у этой прямой очень много других интересных свойств. Пишите в комментариях, стоит ли написать на эту тему отдельную статью. Успехов!

🔍 Видео

Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать

11 класс, 49 урок, Задача ЭйлераСкачать

Точка пересечения высот | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

16 задание. Профильный ЕГЭ 2023. 9 точек окружности, окружность Эйлера. Что это?Скачать

✓ Расстояние от вершины треугольника до точки пересечения высот | Ботай со мной #113 | Борис ТрушинСкачать

Осевая теорема ЭйлераСкачать

Прямая ЭйлераСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

№16 ЕГЭ 2023 по математике. Свойство ортоцентра за 5 минут. Четко и без водыСкачать

Прямая Эйлера (доказательство)Скачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Ортоцентр треугольникаСкачать

Формула Эйлера | Лемма о трезубце | Дополнительные главы школьной геометрииСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Медианы | Свойства медиан | Точка пересечения медиан на прямой ЭйлераСкачать