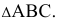Задача на пересечение прямой с плоскостью — это одна из основных задач, с ее применением сталкиваются при рассмотрении сечения тел плоскостями и пересечения поверхностей.
Нахождение точки встречи прямой с плоскостью, заданной пересекающимися прямыми
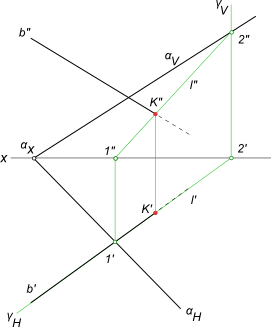
Плоскость и пересекающая ее прямая занимают общее положение.
(γ ∩ α) = l — прямая, пересекающаяся с прямой b.
На пересечение прямой с плоскостью составляем алгоритм нахождения их точки встречи :
1) проводим через b` горизонтальный след γH — горизонтально-проецирующей плоскости γ;
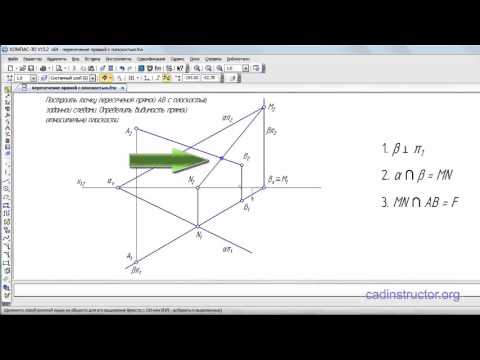
2) определяем фронтальную проекцию линии пересечения l, вспомогательной секущей плоскости γ с данной плоскостью α, используя для этого точки 1` и 2` (принадлежащие данной прямой), в которых горизонтальный след γH пересекает прямые c` и d`;
3) определяем точку K»=l»∩b». Зная K», находим K` на пересечении b` с линией проекционной связи.
Нахождение точки встречи прямой с плоскостью, заданной параллельными прямыми
Задача по нахождению точки встречи прямой с плоскостью заданной следами.
Алгоритм решения не меняется, если плоскость будет задана параллельными прямыми или прямыми, по которым она пересекает плоскости проекций (следы плоскости).
При решении задач на пересечение прямой с плоскостью в качестве вспомогательных плоскостей применяют проецирующие плоскости. Но в случае, например, профильной прямой они бесполезны и тогда надо применить плоскость общего положения.
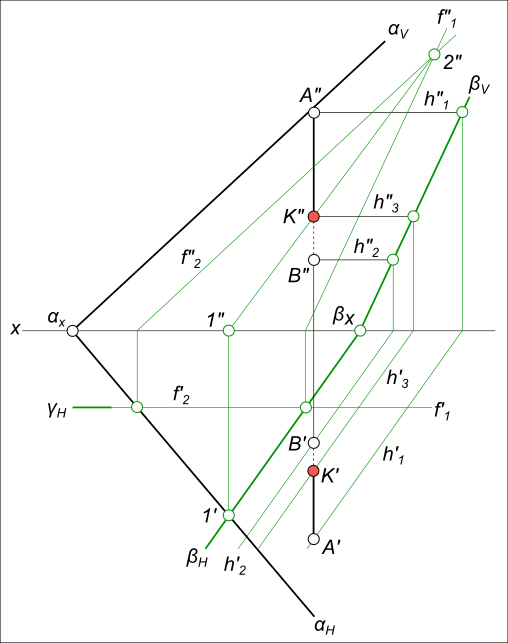
Найти точку встречи профильной прямой AB с плоскостью α заданной следами
Алгоритм выполнения геометрических построений: 1) Заключаем отрезок AB во вспомогательную секущую плоскость общего положения β; 2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости β с данной плоскостью α; 3) Определяем проекцию K» точки K на пересечении 1″-2″ с прямой A»B». Проекция K` точки K может быть найдена: — на пересечении A`B` с 1`-2`; — или как принадлежащая плоскостям α и β.
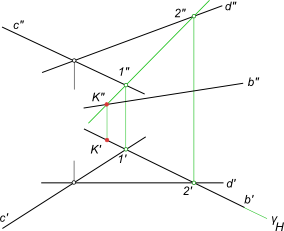
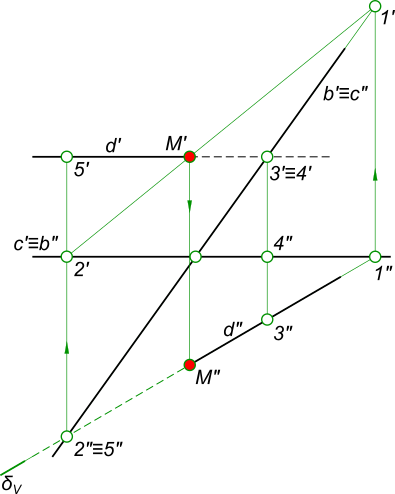
Найти точку встречи прямой d с плоскостью α(b, c), определить видимость
Алгоритм выполнения геометрических построений: 1) Заключаем прямую d во вспомогательную секущую фронтально проецирующую плоскость δ; 2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости δ с данной плоскостью α; 3) Определяем проекцию K` точки K на пересечении 1`-2` с прямой d`. Проекцию K» точки K находим в пересечении d» с линией проекционной связи.
Данный способ решения задачи — найти точку встречи профильной прямой с плоскостью заданной следами применен в статье: Сечение пирамиды плоскостью
Определение видимости пересечения прямой с плоскостью на плоскостях проекций выполняем, используя Конкурирующие точки 2, 3 и 4, 5.
- Построение точки пересечения прямой и плоскости
- Видимость прямой a относительно плоскости α. Метод конкурирующих точек
- Взаимное положение прямой и плоскости с примерами
- Взаимное положение примой и плоскости, двух плоскостей
- Перпендикулярность примой и плоскости
- Перпендикулярности двух плоскостей
- Параллельность прямой и плоскости
- Параллельность двух плоскостей
- Пересечение двух плоскостей
- Пересечение многогранника проецирующей плоскостью
- Взаимное положение двух плоскостей
- Пересечение плоскости общего положения с плоскостью частного положения
- Пересечение двух плоскостей общего положения
- Плоскости параллельны
- Взаимное положение прямой линии и плоскости
- Пересечение прямой линии с плоскостью частного положения
- Определение видимости на эпюрах
- Пересечение прямой линии с плоскостью общего положения
- Прямая параллельна плоскости
- Прямая перпендикулярна плоскости
- Плоскости перпендикулярны
- 📺 Видео
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Построение точки пересечения прямой и плоскости
Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h0α, f0α.
- Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h0γ, f0γ.
- Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B’ = h0α ∩ h0γ, A» = f0α ∩ f0γ. Точки A’ и B» лежат на оси x, их положение определяется по линиям связи.
- Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K’ = a’ ∩ A’B’. Фронтальная проекция K» лежит на прямой a».
Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами.
Видео:Точка встречи прямой с плоскостьюСкачать

Видимость прямой a относительно плоскости α. Метод конкурирующих точек
- Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A» и С» совпадают, но при этом т. A и С удалены от плоскости проекций П2 на разное расстояние.
- Найдем горизонтальные проекции A’ и C’. Как видно на рисунке, точка C’ удалена от плоскости П2 на большее расстояние, чем т. A’, принадлежащая пл. α. Следовательно, участок прямой а», расположенный левее точки K», будет видимым. Участок a» правее K» является невидимым. Отмечаем его штриховой линией.
- Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D’ и E’ совпадают, но при этом т. D и E удалены от плоскости П1 на разное расстояние.
- Определим положение фронтальных проекций D» и E». Как видно на рисунке, точка D», находящаяся в пл. α, удалена от плоскости П1 на большее расстояние, чем т. E», принадлежащая прямой a. Следовательно, участок а’, расположенный правее точки K’, будет невидимым. Отмечаем его штриховой линией. Участок a’ левее K’ является видимым.
Видео:Параллельность прямой к плоскостиСкачать

Взаимное положение прямой и плоскости с примерами
Содержание:
Проекции прямого угла:
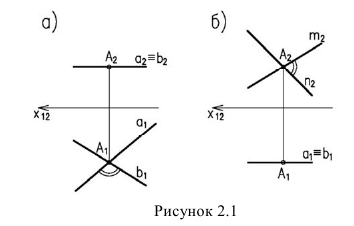
Величина угла между двумя пересекающимися прямыми в общем случае на проекциях искажается. В натуральную величину этот угол будет проецироваться в том случае, если плоскость угла параллельна одной из плоскостей проекций. Тогда другие проекции сторон угла совпадают и параллельны оси проекций (рисунок 2.1).
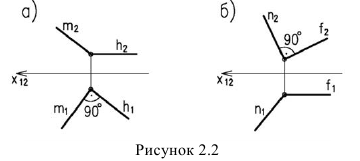
Прямой угол проецируется в натуральную величину, если одна из его сторон параллельна одной из плоскостей проекций (рисунок 2.2).
Видео:Пересечение прямой с плоскостью общего положения. Определение видимости методом конкурирующих точекСкачать
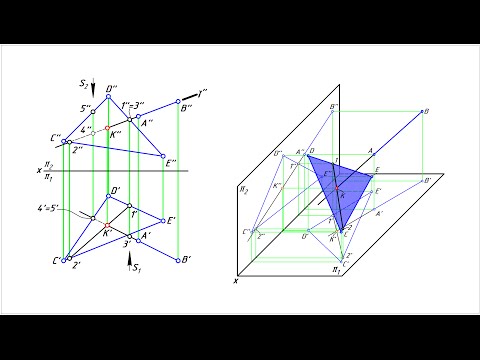
Взаимное положение примой и плоскости, двух плоскостей
Прямая относительно плоскости может занимать следующие положения: лежать в плоскости (что рассматривалось ранее); быть ей параллельна; пересекать плоскость; быть перпендикулярной плоскости (т.е. пересекать под прямым углом).
Две плоскости могут быть:
- взаимно параллельными,
- пересекающимися;
- взаимно перпендикулярными.
Перпендикулярность примой и плоскости
Условие перпендикулярности прямой и плоскости:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым лежащим в этой плоскости.
Так как прямой угол между прямыми линиями проецируется на плоскость проекций без искажения, если одна из прямых параллельна этой плоскости проекций, то пересекающимися прямыми плоскости, которые нужно взять для построения перпендикуляра, могут быть только ее горизонталь и фронталь.
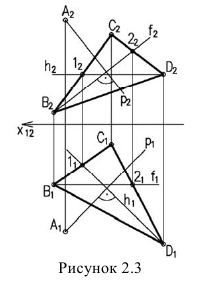
Следовательно, прямая перпендикулярна плоскости, если ее фронтальная проекция перпендикулярна фронтальной проекции фронгали плоскости, а горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали плоскости.
На рисунке 2.3 через точку 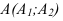
В плоскости 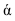
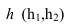
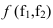
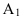
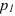
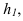
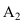
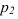
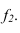
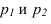
Перпендикулярности двух плоскостей
Две плоскости взаимно перпендикулярны, если одна из них содержи! перпендикуляр к другой.
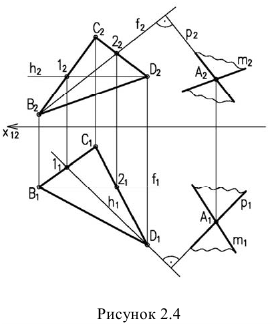
Пусть через данную прямую т необходимо провести плоскость, перпендикулярную плоскости а. заданной треугольником 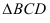
Для решения задачи достаточно на прямой т взять произвольную точку А и провести через нее прямую р, перпендикулярную данной плоскости 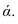
Пересекающиеся прямые m и р образуют плоскость 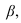
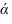
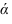
Параллельность прямой и плоскости
Условие параллельности прямой и плоскости:
Прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей этой плоскости.
Рассмотрим пример решения задачи на параллельности прямой и плоскости.
Задача: построить фронтальную проекцию прямой n, проходящей через точку А и параллельной
Для решения задачи:
Проводим горизонтальную проекцию прямой 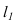
Строим фронтальную проекцию
Через точку 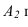
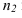
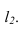
Параллельность двух плоскостей
Условие параллельности двух плоскостей:
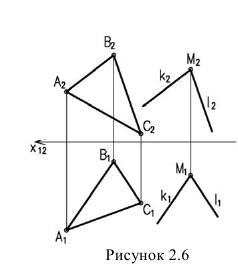
- две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
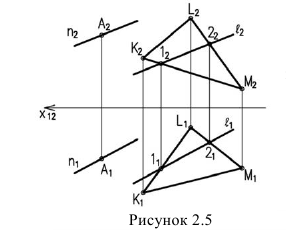
Изображенные на рисунке 2.6 плоскости 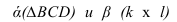
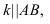
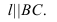
Задача на нахождение точки пересечения прямой линии с плоскостью является первой основной позиционной задачей курса начертательной геометрии.
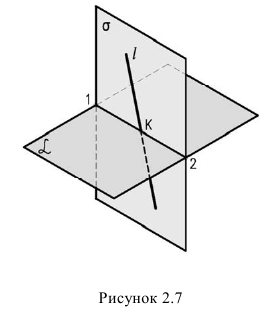
Алгоритм решения задачи (рисунок 2.7):
1. Прямую 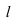
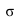
2. Находим линию пересечения (1-2) вспомогательной плоскости с заданной
3. Отмечаем точку пересечения К найденной линии пересечения (1-2) с заданной прямой
4. Определяем видимость прямой 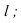
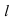
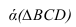
Пересечение двух плоскостей
Две плоскости пересекаются по прямой линии, поэтому для её построения достаточно найти две точки одновременно принадлежащие двум плоскостям.
Рассмотрим несколько случаев построения линии пересечения двух плоскостей.
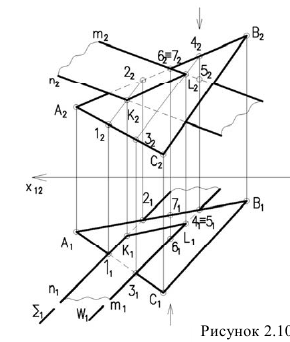
1-й случай — пластины непрозрачные заданы с нахлёстом (рисунок 2.10).
Задача сводится к нахождению точек пересечения прямых m и n с плоскостью а. 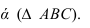
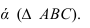
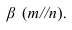
2-й случай — плоскости заданы на некотором расстоянии, что не дает возможность определить линии пересечения двух плоскостей первым способом. В этом случае используется метод плоскостей-посредников.
Алгоритм решения задачи (рисунок 2.11):
- Заданные плоскости
рассекаем вспомогательной плоскостью посредником
- Определяем линию пересечения 1-2 плоскости а с плоскостью а и линию пересечения 3-4 плоскости
с плоскостью
- Определяем точку К — точку пересечения линий 1-2 и 3-4, принадлежащую плоскостям
- Аналогичным образом находим точку L с помощью плоскости посредника
- Соединив две точки К и М, получим линию пересечения двух плоскостей
Видимость при этом не определяется.
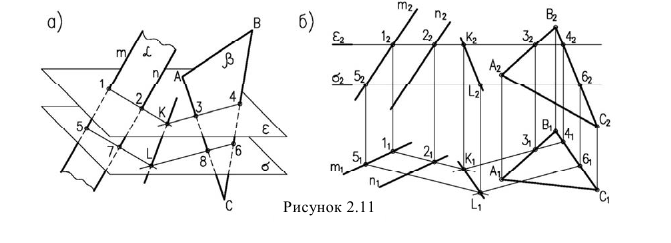
3-й случай — пересекающиеся плоскости общего положения заданы следами пересекающимися в пределах чертежа (рисунок 2.12).
В данном случае в качестве плоскостей-посредников могут быть использованы плоскость проекций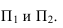
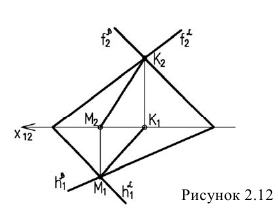
Пересечение многогранника проецирующей плоскостью
Так как секущая плоскость горизонтально-проецирующая, то фронтальную проекцию сечения можно построить, определив точку пересечения каждого ребра с плоскостью о (рисунок 2.13)
Взаимное положение двух плоскостей
Две плоскости могут принадлежать одна другой; быть параллельны или пересекаться.
Пересечение плоскостей. Линия пересечения двух плоскостей -прямая. Положение прямой в пространстве определяют две точки. Чтобы найти линию пересечения плоскостей, достаточно знать две точки, принадлежащие двум плоскостям одновременно.
Пересечение плоскости общего положения с плоскостью частного положения
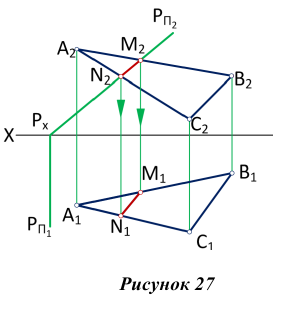
На рис. 27 показано построение линии пересечения фронтально-проецирующей плоскости Р с плоскостью треугольника AВС.
Так как линия пересечения двух плоскостей принадлежит фронтально-проецирующей плоскости Р, то ее фронтальная проекция 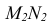
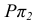
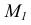
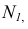
Пересечение двух плоскостей общего положения
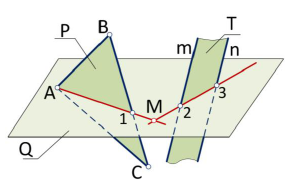
Задача. Построить линию пересечения двух плоскостей общего положения
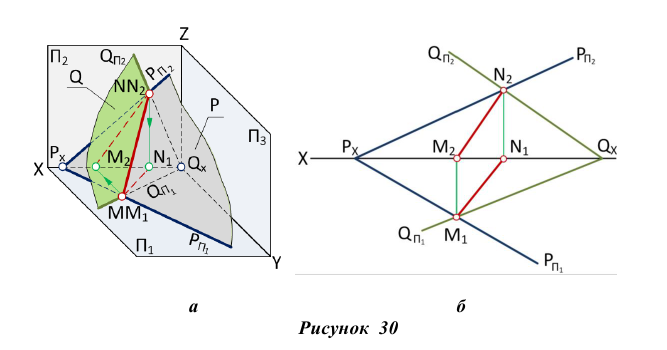
Алгоритм решения задачи (рис. 28)
- Вводим вспомогательную секущую плоскость Q общего положения
- Находим линии пересечения вспомогательной плоскости Q с двумя заданными Р и Т:
- Определяем точку пересечения построенных линий:
Точка М принадлежит одновременно плоскостям Р и Т, следовательно, она принадлежит линии их пересечения.
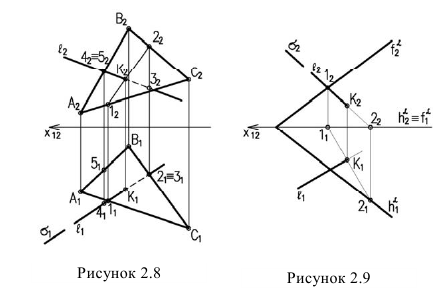
- Для нахождения второй общей точки вводим еще одну секущую плоскость и повторяем построения (п.2, п.З). Решение этой задачи на эпюре показано на рис. 29:
Согласно алгоритму решения задачи проводим вспомогательные секущие плоскости частного положения 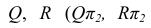
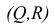
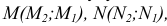
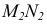
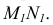
Плоскости параллельны
Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.
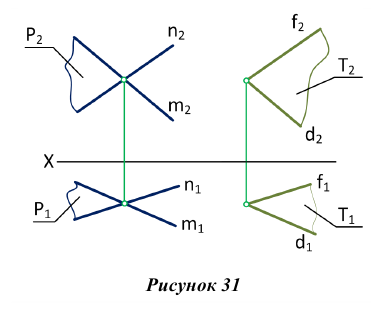
Изображенные на рис. 31 плоскости 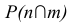
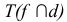
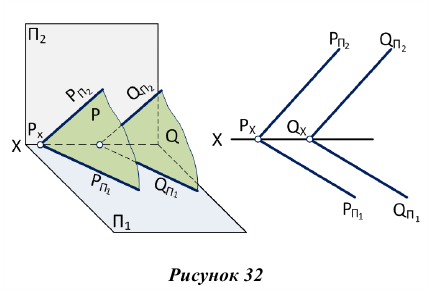
Плоскости общего положения также параллельны, если два любых одноименных следа параллельны между собой.
Изображенные на рис. 32 плоскости Р и Q параллельны, т.к.
Взаимное положение прямой линии и плоскости
Прямая может лежать в плоскости, пересекать плоскость и быть параллельной плоскости.
Пересечение прямой линии с плоскостью частного положения
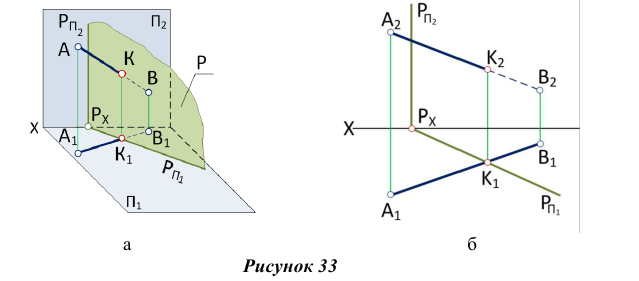
Если заданная плоскость перпендикулярна к какой-либо плоскости проекций (рис.33, а), то она проецируется на эту плоскость проекций в виде прямой линии, на которой обязательно будут находиться соответствующие проекции всех точек, принадлежащих данной плоскости, в том числе и проекции точки пересечения какой-то прямой с заданной плоскостью (точка встречи прямой с плоскостью). Поэтому точка встречи прямой с плоскостью частного положения находится па эпюре без дополнительных построений (рис. 33,6).
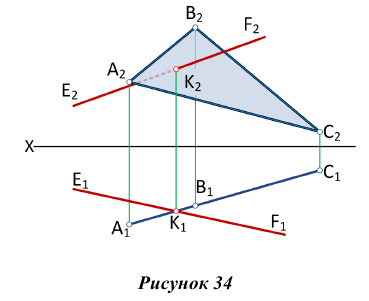
На рис. 34 точка встречи прямой EF с горизонтально-проецирующей плоскостью, заданной треугольником ABC, является точкой пересечения горизонтальных проекций 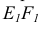
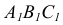
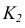
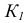
Определение видимости на эпюрах
Вопрос о видимости линий или поверхностей всегда может быть сведен к вопросу о видимости точек. Если несколько точек находятся на общей для них линии связи, то видимой будет только одна из них — наиболее удаленная от той плоскости проекций, по отношению к которой определяется видимость.
Точки, расположенные на одной линии связи, называются конкурирующими. Точки А, В и С, D — конкурирующие (рис. 35).
Относительно плоскости проекций 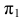
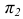
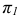
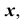
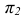
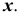
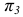
Пересечение прямой линии с плоскостью общего положения
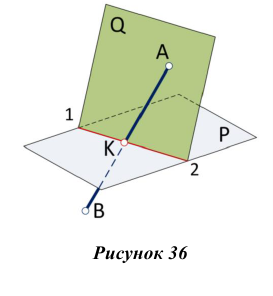
Точку пересечения прямой линии АВ с плоскостью общего положения Р (рис. 36) находят следующим образом:
- а) через заданную прямую АВ проводим некоторую вспомогательную плоскость Q, обычно плоскость частного положения;
- б) строим линию пересечения 1-2 заданной плоскости Р и вспомогательной Q;
- в) находим положение точки пересечения данной прямой АВ и линии пересечения 1-2 плоскостей (точки К).
- г) определяем видимость прямой АВ по отношению к плоскости Р.
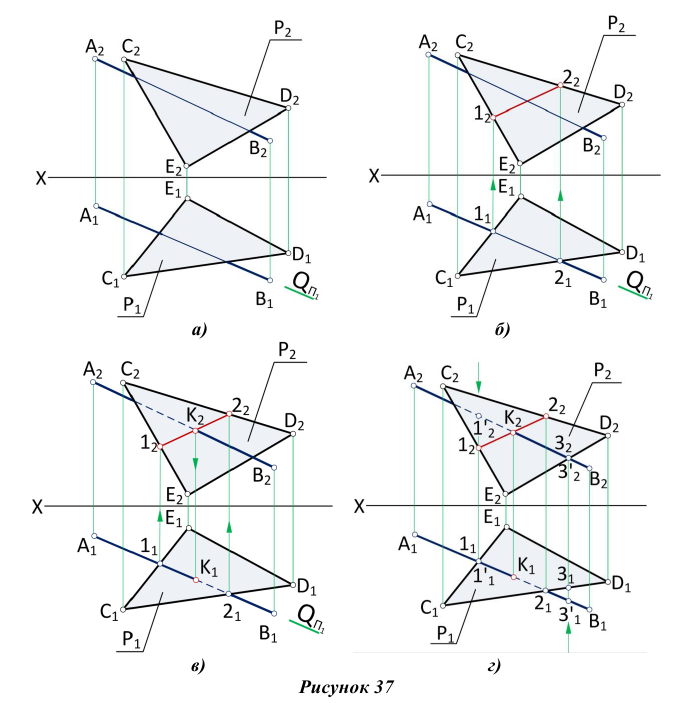
Пошаговые построения по определению точки пересечения прямой АВ с плоскостью треугольника CDE на эпюре приведены на рис. 37 (а-в).
Видимость прямой АВ относительно плоскости Р (рис. 37,г) определяем с помощью двух пар конкурирующих точек 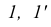
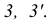
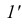
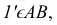
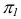
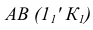
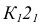
Аналогично, используя конкурирующие точки 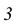
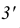
Задачи, на построение линии пересечения плоскостей, заданных пересекающимися прямыми, можно решать подобно задаче на пересечение прямой с плоскостью.
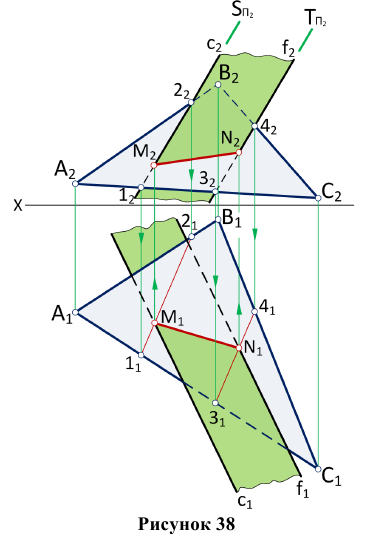
Одна из изображенных на рис. 38 плоскостей задана треугольником AВС, а вторая — двумя параллельными прямыми с и f.
Линия пересечения этих плоскостей (линия MN) определена при помощи построения точек встречи прямых с и f с плоскостью треугольника. Для этого через прямую с проведена фронтально — проецирующая плоскость S. Прямая 1-2 — линия пересечения плоскости треугольника с вспомогательной фронтально-проектирующей плоскостью S. Точка М — точка встречи прямой с с плоскостью треугольника AВС.
Точка N найдена аналогично. Прямая MN — искомая. Видимость на рис. 86 определена из условия, что заданные плоскости ограничены треугольником и двумя параллельными прямыми, определяющими их.
Прямая параллельна плоскости
Если прямая линия параллельна какой-либо прямой, находящейся в плоскости, то она параллельна этой плоскости. Следовательно, для построения прямой, параллельной заданной плоскости, надо взять в этой плоскости какую — либо прямую и построить ей параллельную.
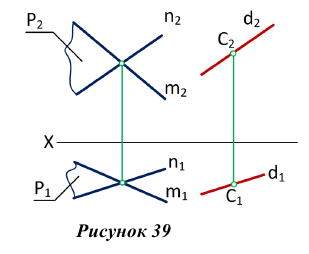
На рис. 39 через точку С проведена прямая d, параллельная плоскости Р, заданной пересекающимися прямыми т и п.
Прямая d параллельна прямой n, принадлежащей плоскости 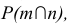
Прямая перпендикулярна плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Чтобы построить перпендикуляр из точки D на плоскость треугольника AВС (рис.40) необходимо предварительно построить
горизонталь 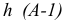
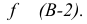
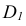
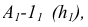
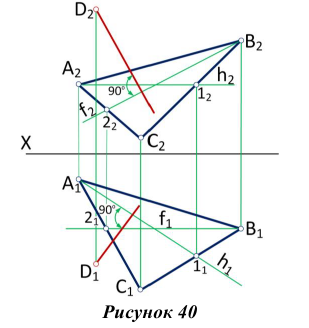
Если же плоскость задана следами, то, учитывая, что фронтальная проекция любой фронтали в этой плоскости всегда параллельна фронтальному следу плоскости, а горизонтальная проекция любой горизонтали параллельна горизонтальному следу плоскости, легко видеть (рис. 41), что проекции перпендикуляра к плоскости должны быть перпендикулярны соответствующим следам плоскости.
Плоскости перпендикулярны
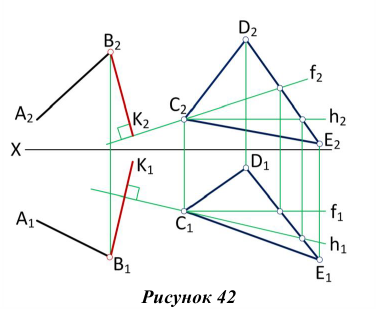
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. На рис. 42 через прямую АВ проведена плоскость, перпендикулярная плоскости треугольника CDE. Для этого из точки В прямой АВ восстановлен перпендикуляр ВК к плоскости треугольника 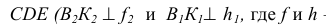
Если возникает необходимость в построении взаимно перпендикулярных прямых общего положения, необходимо построить плоскость, перпендикулярную заданной прямой, и взять в ней любую прямую.
Задача.
Через точку М провести прямую, перпендикулярную прямой
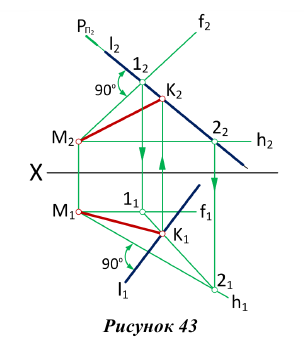
Для построения взаимно перпендикулярных прямых (рис. 43), одна из которых 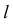
- а) через заданную точку M проводим плоскость
перпендикулярную заданной прямой
- б) находим точку пересечения заданной прямой
с построенной плоскостью Q — точку К (для этого прямую
заключаем во вспомогательную фронтально -проецирующую плоскость Р);
- в) соединяем заданную точку М с найденной точкой К прямой линией. Эта линия МК и будет искомой.
Задача:
Определить расстояние от точки до плоскости, заданной треугольником ABC (рис.44)
Расстояние от точки до плоскости определяется длиной перпендикуляра, опущенного из точки на плоскость. Поэтому решение этой задачи выполняем в следующей последовательности:
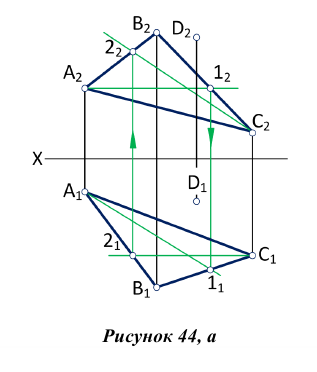
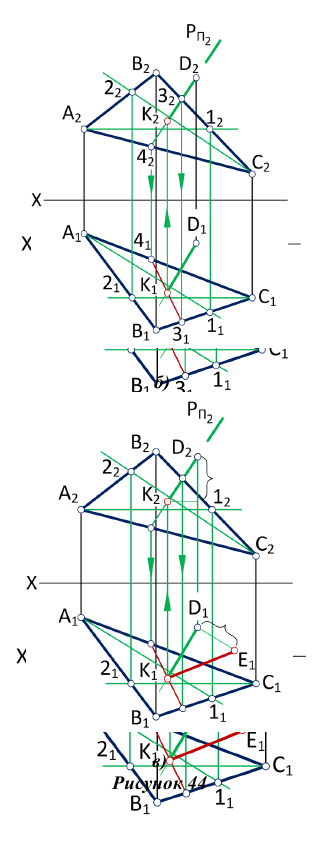
1. Из точки D опускаем перпендикуляр на плоскость треугольника AВС (рис.44, а), для этого в плоскости треугольника проводим горизонталь 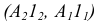
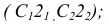
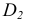
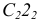
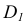
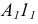
2. Находим точку пересечения перпендикуляра с плоскостью 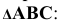
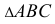
3. Методом прямоугольного треугольника определяем натуральную величину отрезка DK, для чего в плоскости 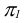
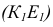
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Решение метрических задач
- Тени в ортогональных проекциях
- Кривые поверхности
- Пересечения криволинейных поверхностей
- Образование и задание поверхности на чертеже
- Пересечение поверхности плоскостью и прямой
- Развертки поверхностей
- Способы преобразования проекций
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📺 Видео
Линия пересечения плоскостейСкачать

Параллельность прямой и плоскости. 10 класс.Скачать

Пересечение прямой и плоскостиСкачать

Построение точки пересечения прямой с плоскостью, заданной следамиСкачать
Пересечение прямой и плоскостиСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Пересечение прямой линии с плоскостью Определение видимости прямойСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Найти точку пересечения прямой и плоскостиСкачать

23. Точка пересечения прямой и плоскости / Проекция точки на плоскость / Проекция точки на прямуюСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

Пересечение прямой и плоскости Определение видимости прямойСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Следы прямойСкачать

Лекция 2. Основная задача начертательной геометрии. Точка пересечения прямой с плоскостью.Скачать



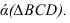
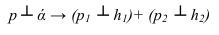
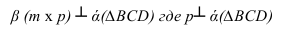
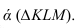
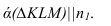
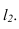
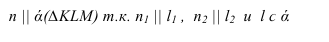
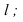
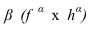
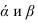 рассекаем вспомогательной плоскостью посредником
рассекаем вспомогательной плоскостью посредником 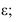
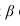 с плоскостью
с плоскостью 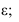
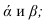
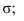
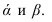
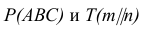
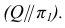
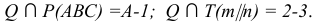
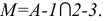 Точка М принадлежит одновременно плоскостям Р и Т, следовательно, она принадлежит линии их пересечения.
Точка М принадлежит одновременно плоскостям Р и Т, следовательно, она принадлежит линии их пересечения.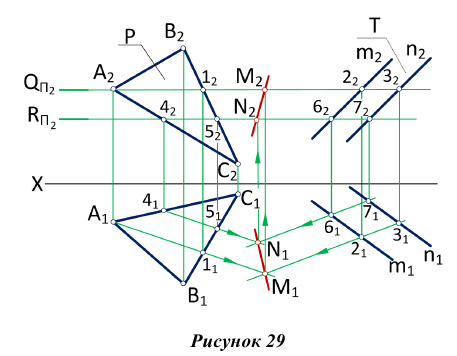
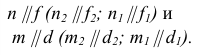
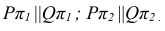
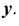
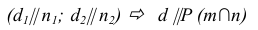
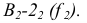
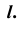
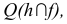 перпендикулярную заданной прямой
перпендикулярную заданной прямой 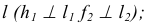
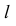 с построенной плоскостью Q — точку К (для этого прямую
с построенной плоскостью Q — точку К (для этого прямую 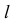 заключаем во вспомогательную фронтально -проецирующую плоскость Р);
заключаем во вспомогательную фронтально -проецирующую плоскость Р);