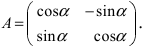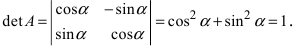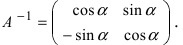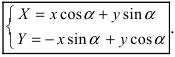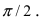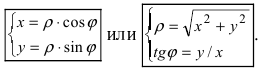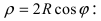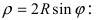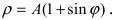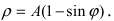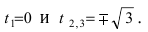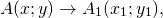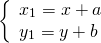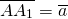Перенос окружности параллельным переносом (2 видео)

Преобразования декартовой системы координат с примерами решения

Содержание:

Содержание

Преобразования декартовой системы координат
Параллельный перенос и поворот системы координат
Полярные координаты. Замечательные кривые
Параллельный перенос
Метод параллельного переноса
💥 Видео

Видео:Геометрия и группы. Алексей Савватеев. Лекция 2.3. Параллельный переносСкачать

Преобразования декартовой системы координат

Параллельный перенос и поворот системы координат

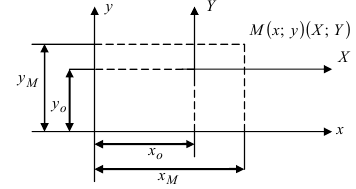
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):

Рис. 46. Параллельный перенос одной системы координат относительно другой системы.

Систему координат

Пример:

Дана точка М(3;2) и начало новой системы координат 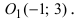Вычислить положение точки М в новой системе отсчета.

Решение:

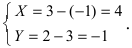
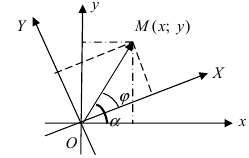
Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим Следовательно, точка М в новой системе отсчета имеет координаты М(4; -1).

2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 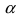(Рис. 47):

Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.

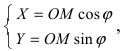
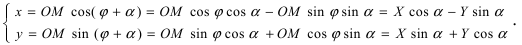
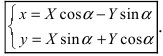
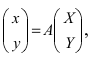
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны а координаты этой точки в старой системе координат равны Таким образом формулы перехода от новых координат произвольной точки М к старым имеет вид В матричном виде эти равенства можно записать в виде где матрица перехода

Найдем обратное преобразование системы координат, найдем матрицу 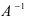обратную к матрице А:

Найдем алгебраические дополнения всех элементов

Запишем обратную матрицу

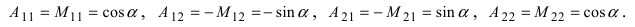
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.

Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.

Таким образом, имеем 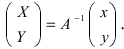Следовательно, формулы перехода от старой системы отсчета к новой системе отсчета имеют вид:

Пример:

Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол

Решение:

Воспользуемся полученными формулами 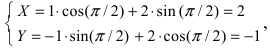т.е. в новой системе координат точка имеет координаты М(2; -1).

Рассмотрим применение преобразования координат:

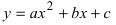
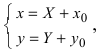
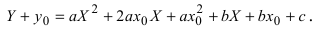
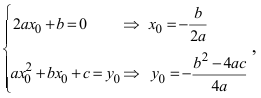
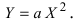
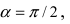
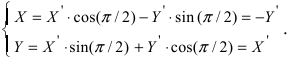
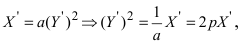
а) Преобразовать уравнение параболы к каноническому виду. Проведем параллельный перенос системы координат получим Выберем начало отсчета новой системы координат так, чтобы выполнялись равенства тогда уравнение принимает вид Выполним поворот системы координат на угол тогда Подставим найденные соотношения в уравнение параболы где параметр параболы

Пример:

Преобразовать уравнение параболы 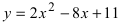к каноническому виду.

Решение:

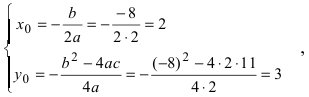
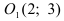
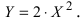
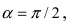
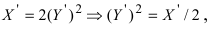
Найдем начало отсчета новой системы координат после параллельного переноса т.е. точка — начало координат новой системы отсчета. В этой системе уравнение параболы имеет вид Проведем поворот системы отсчета на угол тогда

следовательно, параметр параболы р = 1/4.

б) Выяснить, какую кривую описывает функция

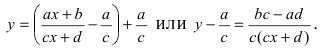
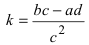
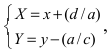
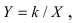
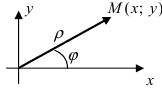
Проведем следующее преобразование Производя параллельный перенос системы координат, вводя обозначение

и новые координаты получим уравнение которое описывает равнобочную гиперболу.

Полярные координаты. Замечательные кривые

Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 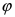между радиус-вектором и полярной осью (угол отсчитывается против часовой стрелки).

Рис. 48. Полярная система координат.

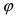
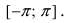
Главными значениями угла являются значения, лежащие в интервале Из рисунка видно, что декартовы и полярные координаты связаны формулами

Рассмотрим замечательные кривые в полярной системе координат:

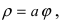
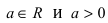
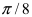
1. Спираль Архимеда где число (Рис. 49). Для построения кривой в полярной системе координат, разобьем декартову плоскость лучами с шагом по углу и на каждом луче отложим ему соответствующее значение р.

Рис. 49. Спираль (улитка) Архимеда.

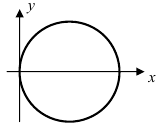
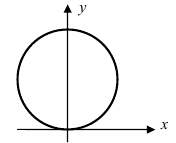
2. Уравнение окружности: уравнение 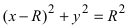описывает окружность с центром в точке A(R; 0) и радиусом R (Рис. 50). В полярной системе координат уравнение принимает вид

Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.

3. Уравнение 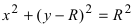описывает окружность с центром в т. А(0; R) и радиусом R (Рис. 51). В полярной системе координат уравнение принимает вид

Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.

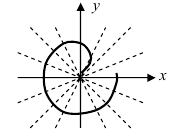
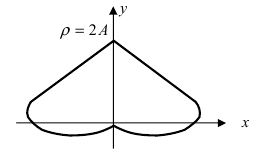
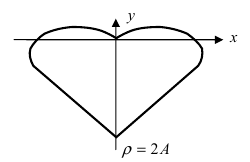
4. Кардиоиды:

Рис. 52. Кардиоида

Рис. 53. Кардиоида

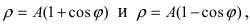
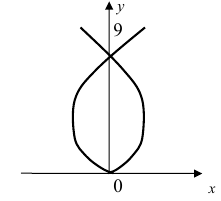
Аналогично выглядят кардиоиды но они вытянуты вдоль оси абсцисс Ох.

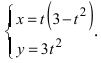
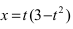
5. Петля: Величина равна нулю при

Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид

Рекомендую подробно изучить предметы:

Математика
Алгебра
Линейная алгебра
Векторная алгебра
Высшая математика
Дискретная математика
Математический анализ
Математическая логика

Ещё лекции с примерами решения и объяснением:

Бесконечно малые и бесконечно большие функции
Замечательные пределы
Непрерывность функций и точки разрыва
Точки разрыва и их классификация
Экстремум функции
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Скалярное произведение и его свойства
Векторное и смешанное произведения векторов

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:9 класс, 32 урок, Параллельный переносСкачать

Параллельный перенос

Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.

Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.

1) Введём на плоскости декартовы координаты x, y.

Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.

Формулы параллельного переноса

Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1)

то параллельный перенос задаётся формулами:

Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.

2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:

Свойства параллельного переноса

1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).

2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).

4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.

В алгебре параллельный перенос широко используется для построения графиков функций.

Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Метод параллельного переноса

Перейдем сразу к решению задач на построение методом параллельного переноса.

Задача 6.34. Даны две окружности F_v F₂ и прямая I. Провести прямую, параллельную прямой I, на которой окружности F_r и F₂ высекают равные хорды.

Пусть прямая V искомая, т.е. прямая V высекает на данных окружностях равные хорды АВ иА’В’ (рис. 6.34).

Тогда точки АиА’,ВиВ’ можно рассматривать как соответственные при параллельном переносе О_хО<.

Так как точка А’ является образом точки А, принадлежащей окружности F_b то точка Л’ принадлежит образу окружности F,. Следовательно, А’ — общая точка окружности F₂ и образа окружности Fj при параллельном переносе 0-[0[. Построив точку А’, находим на окружности F] ее прообраз. _

Если F₂ есть образ точки F_x при параллельном переносе OjOf, то задача имеет бесконечное множество решений. В остальных случаях задача имеет не более четырех решений, так как окружность F₂ имеет не более двух точек пересечения с окружностью F <и не более двух точек пересечения с окружностью F» (образ окружности Fj при параллельном переносе О_уО<).

Задача 6.35. Между двумя данными окружностями (О, Р) и (Q, г) провести отрезок данной длины (а) параллельно данной прямой (АР).

Анализ. Допустим, что задача решена и отрезок CD является искомым (рис. 6.35). Если мысленно будем перемещать отрезок CD параллельно самому себе, оставляя один из его концов D скользящим по данной окружности (Q, г), то ясно, что другой конец (С) отрезка CD опишет в это время окружность того же радиуса (г), имеющую центр в некоторой точке Р, отстоящей от точки Q на расстояние, равное отрезку а. Отсюда следует, что, построив окружность (Р, г), мы сможем построить и искомые отрезки.

Построение. 1. Проведем из точки Q отрезок QP, который параллелен прямой АВ и равен отрезку а.

2. Около точки Р радиусом, равным г, опишем вспомогательную окружность (Р, г).
3. Обозначим буквами С и ? те точки, в которых вспомогательная окружность (Р, г) пересечет окружность (О, Р).
4. Если из точек С и ? проведем прямые, параллельные прямой АВ, то они пересекут окружность (Q, г) в некоторых точках D и F.

Отрезки CD и ?? — искомые.

Доказательство несложное, а поэтому предлагаем провести самостоятельно.

Исследование. Если вспомогательная окружность (Р, г) пересекает данную окружность (О, К), то задача имеет два решения.

Если окружность (Р, г) будет лишь касаться окружности (О, Р), то задача имеет одно решение.

Наконец, если окружность (Р, г) не будет ни касаться окружности, ни пересекать ее, то задача не имеет решений.

Задача 6.36. Даны окружность и прямая I. На окружности даны две точки А и В. Найти на окружности такую точку М, чтобы прямые МА и МВ пересекали I в точках К и N таким образом, что KN — а, где а — заданный отрезок.

Построим точку А’ (рис. 6.36) так, чтобы NKAA’ был параллелограммом (А’ получается из А при помощи известного параллельного переноса). Поскольку ZBNA’ = ZBMA, а последний известен, то точка N находится как пересечение I с соответствующим геометрическим местом точек. Следует также рассмотреть случай расположения точки М на другой дуге АВ.