Содержание:
В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.
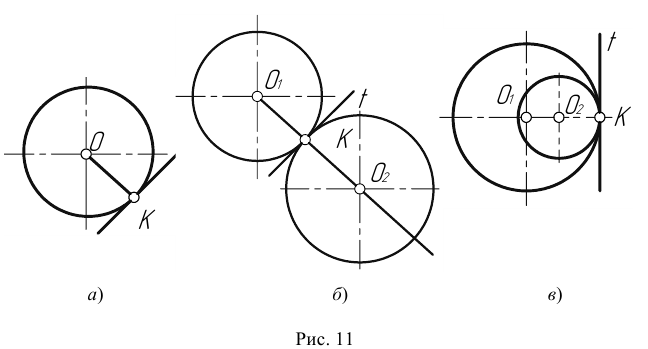
- Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
- Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).
Точка касания К и центры окружностей
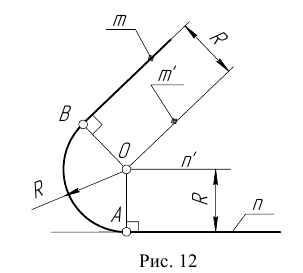
- Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
- Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
- Дуга сопряжения АВ – это дуга окружности, с помощью которой выполняется сопряжение (рис. 12).
- Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).
Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.
- Сопряжение двух пересекающихся прямых линий
- Сопряжения прямой с окружностью
- Сопряжение двух окружностей
- Построение касательных
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Касательная к окружности
- Касательная к окружности, секущая и хорда — в чем разница
- Свойства касательной к окружности
- Задача
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- 🌟 Видео
Видео:Касательные к окружностиСкачать

Сопряжение двух пересекающихся прямых линий
Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.
Выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от прямой n на расстояние радиуса R сопряжения. Таким множеством является прямая
параллельная данной прямой n и отстоящая от неё на расстояние R.
- Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения. Таким множеством является прямая
параллельная m и отстоящая от последней на расстояние R.
- В пересечении построенных прямых
найдем центр сопряжения О.
- Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.
Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.
Видео:Внешняя касательная к двум окружностямСкачать
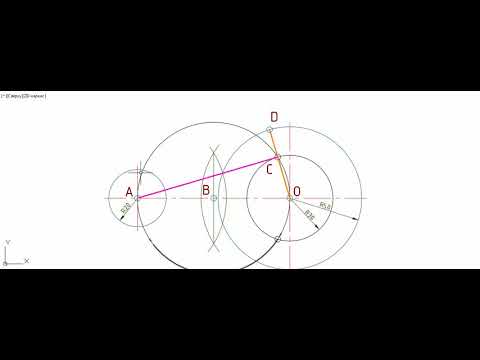
Сопряжения прямой с окружностью
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.
Пример 1. Пусть задана окружность радиусом R с центром в точке 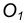
Для решения задачи выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая
параллельная m и отстоящая от неё на расстояние R.
- Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность
проведенная радиусом
- Центр сопряжения О находим как точку пересечения линий
- Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
- Проведем дугу сопряжения АВ.
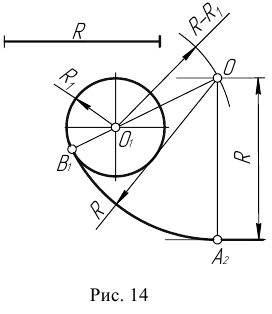
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 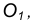
Видео:Построение внешней касательной к двум дугам окружностей. Урок11.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
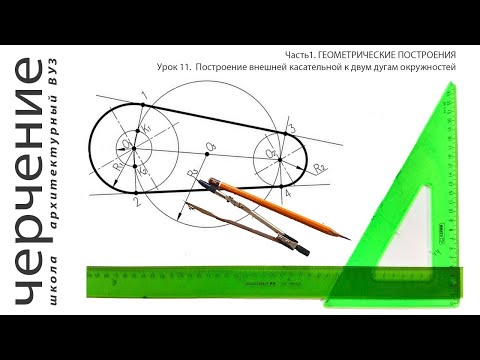
Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 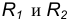
- Для нахождения центра сопряжения О проведем окружность
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
равен
- Радиусом
проведем окружность
, удаленную от данной окружности n на расстояние R.
- Найдем центр сопряжения О как точку пересечения окружностей
.
- Найдем точку сопряжения А как пересечение линии центров
с дугой m.
- Аналогично найдем точку В как пересечение линии центров
с дугой n .
- Проведем дугу сопряжения АВ.
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами 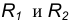
- Для нахождения центра сопряжения О проведем окружность
на расстоянии
от данной окружности m.
- Проведем окружность
на расстоянии
от данной окружности n.
- Центр сопряжения О найдем как точку пересечения окружностей
- Точку сопряжения А найдем как точку пересечения линии центров
с заданной окружностью m.
- Точку сопряжения В найдем как точку пересечения линии центров
c заданной окружностью n.
- Проведем дугу сопряжения AВ с центром в точке O.
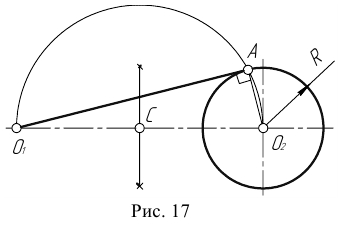
Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.
Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Построение касательных
Пример 1. Дана окружность с центром в точке 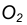
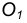
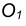
Для решения задачи выполним следующие построения.
- Соединим точку
с центром окружности
- Находим середину С отрезка
- Из точки С, как из центра, проведем вспомогательную окружность радиусом
- В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку
с точкой А.
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 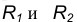
- Находим середину С отрезка
- Из точки С, как из центра, радиусом
проведем вспомогательную окружность.
- Из центра большей окружности
проведем вторую вспомогательную окружность радиусом
- Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус
идущий в точку касания В. 5. Для построения второй точки касания А проведем
- Соединим точки А и В отрезком прямой линии.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Нанесение размеров на чертежах
- Резьба на чертеже
- Соединения разъемные и неразъемные в инженерной графике
- Виды конструкторских документов
- Виды в инженерной графике
- Разрезы в инженерной графике
- Сечения в инженерной графике
- Выносные элементы в инженерной графике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Построение внутренней касательной к двум дугам окружностей.Урок12.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
 | ||
| Внешнее касание двух окружностей | ||
 | ||
| Внутреннее касание двух окружностей | ||
 | ||
| Окружности пересекаются в двух точках | ||
 | ||
 | ||
| Каждая из окружностей лежит вне другой | ||
 Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
 Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
 | ||||
| Внутренняя касательная к двум окружностям | ||||
 | ||||
| Общая хорда двух пересекающихся окружностей | ||||
 | ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Окружность по двум другим окружностям.mp4Скачать  Касательная к окружностиО чем эта статья: Видео:Касательные к двум окружностям.Скачать  Касательная к окружности, секущая и хорда — в чем разницаВ самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу. |
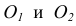
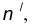 параллельная данной прямой n и отстоящая от неё на расстояние R.
параллельная данной прямой n и отстоящая от неё на расстояние R.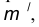 параллельная m и отстоящая от последней на расстояние R.
параллельная m и отстоящая от последней на расстояние R.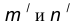 найдем центр сопряжения О.
найдем центр сопряжения О.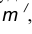 параллельная m и отстоящая от неё на расстояние R.
параллельная m и отстоящая от неё на расстояние R.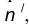 проведенная радиусом
проведенная радиусом 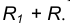
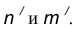
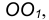 т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.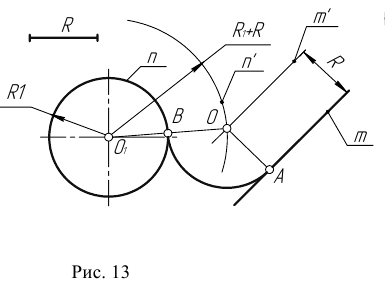
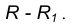
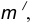 удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности 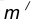 равен
равен 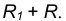
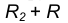 проведем окружность
проведем окружность 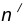 , удаленную от данной окружности n на расстояние R.
, удаленную от данной окружности n на расстояние R.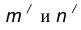 .
.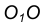 с дугой m.
с дугой m.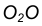 с дугой n .
с дугой n .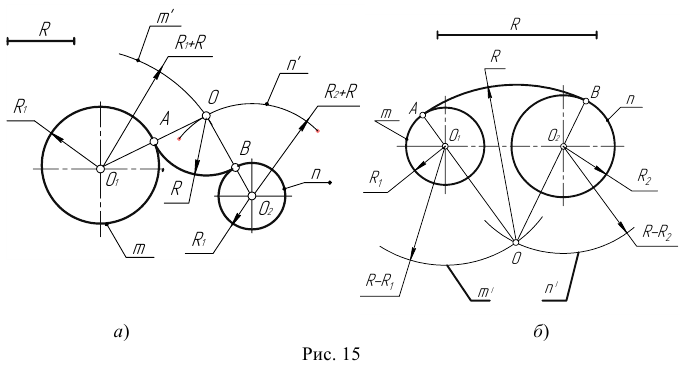
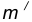 на расстоянии
на расстоянии 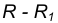 от данной окружности m.
от данной окружности m.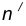 на расстоянии
на расстоянии 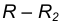 от данной окружности n.
от данной окружности n.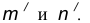
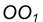 с заданной окружностью m.
с заданной окружностью m.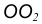 c заданной окружностью n.
c заданной окружностью n.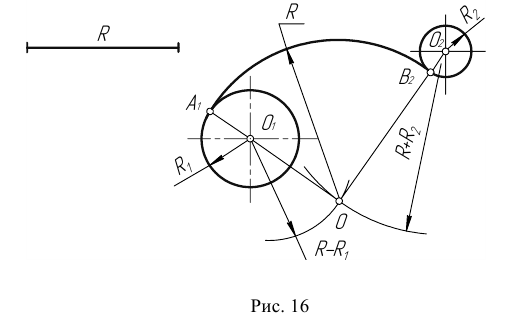
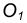 с центром окружности
с центром окружности 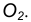
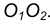
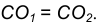
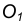 с точкой А.
с точкой А.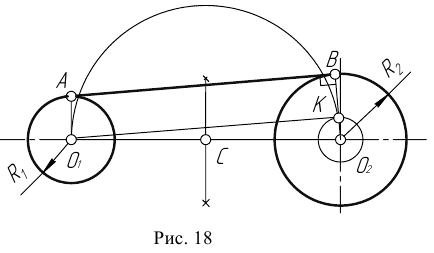
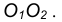
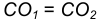 проведем вспомогательную окружность.
проведем вспомогательную окружность.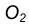 проведем вторую вспомогательную окружность радиусом
проведем вторую вспомогательную окружность радиусом 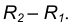
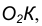 идущий в точку касания В. 5. Для построения второй точки касания А проведем
идущий в точку касания В. 5. Для построения второй точки касания А проведем