- Что значит вычислить двойной интеграл в полярных координатах?
- Пределы интегрирования в повторных интегралах
- Случай первый
- Случай второй
- Случай третий
- Случай четвёртый
- Решения двойных интегралов в полярных координатах: примеры
- Переход к полярным координатам в двойном интеграле окружность
- Контакты
- Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам
- Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам
- Далее:
- 🎥 Видео
Видео:Двойной интеграл в полярных координатахСкачать
Что значит вычислить двойной интеграл в полярных координатах?
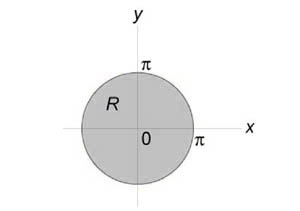
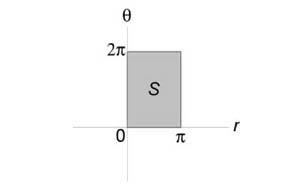
Если область интегрирования представляет собой окружность или часть окружности, двойной интеграл проще вычислить не в декартовых прямоугольных координатах, а в полярных координатах. В этом случае подынтегральная функция выражается как функция полярных переменных r и φ с использованием соотношений между полярными и декартовыми координатами x = rcosφ и y = rsinφ :
.
Что представляет собой элемент площади dxdy , выраженный в полярных координатах? Для ответ на этот вопрос разделим область интегрирования D на участки линиями окружности r = const и лучами φ = const . Рассмотрим один частичный участок (заштрихованный на рисунке), который ограничивают лучи, образующие с полярной осью углы φ и φ + dφ и линии окружности с радиусом r и r + dr . Этот криволинейный четырёхугольник можем приближенно считать прямоугольником с длиной боковой стороны dr и длиной основания rdφ . Поэтому элемент площади в полярных координатах выражается следующим образом:
а двойной интеграл в полярных координатах записывается так:
.
Чтобы вычислить двойной интеграл в полярных координатах, его нужно выразить через повторные интегралы, так же, как и «обычный» двойной интеграл в декартовых прямоугольных координатах. В полярных координатах внешний интеграл всегда интегрируется по углу φ , а внутренний — по радиусу r .
Вычислить двойной интеграл в полярных координатах — значит, как и в декартовых прямоугольных координатах, найти число, равное площади упомянутой фигуры D .
Видео:Перейти к полярным координатам в двойном интегралеСкачать
Пределы интегрирования в повторных интегралах
При переходе от двойного интеграла в полярных координатах к повторным интегралам расстановку пределов интегрирования могут облегчить следующие закономерности.
Случай первый
Полюс O является внутренней точкой области интегрирования D , область ограничена линией r = r(φ) .
Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны 0 и 2π , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:
.
Случай второй
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , но не является угловой точкой.
Через полюс O проведём касательную. Пусть касательная образует с полярной осью угол α . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и π + α , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:
.
Случай третий
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , и является угловой точкой.
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:
.
Случай четвёртый
Полюс O находится вне области интегрирования D .
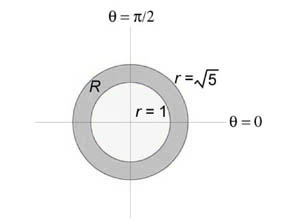
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β , а область D ограничивают линии r = r 1 (φ) и r = r 2 (φ) . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — r 1 (φ) и r 2 (φ) . Переход к повторным интегралам осуществляется следующим образом:
.
Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать
Решения двойных интегралов в полярных координатах: примеры
Пример 1. Вычислить в полярных координатах двойной интеграл
,
где область D ограничена линиями 
, 
, 
.
Решение. Строим на чертеже область интегрирования. Видим, что этот пример относится к третьему случаю из вышеописанных четырёх случаев расположения области интегрирования.
Выразим подынтегральную функцию как функцию полярных переменных:
.
Данные в условии линии, ограничивающие D , приводим к полярным координатам:
Переходим от двойного интеграла к повторному, учитывая пределы интегрирования, верные в третьем случае:
.
Вычисляем интеграл (так как повторные интегралы независимы друг от друга, каждый из них вычисляем отдельно и результаты перемножаем):
Пример 2. В повторном интеграле
перейти к полярной системе координат.
Решение. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y — от параболы x² до 1. Таким образом, область интегрирования снизу ограничена параболой y = x² , а сверху — прямой y = 1 . Область интегирования изображена на следующем чертеже.
При переходе к полярным координатам область интегрирования нужно разделить на три части. Значит, данный повторный интеграл должен быть вычислен как сумма трёх интегралов. В первой области полярный радиус меняется от 0 до параболы, во второй области — от 0 до прямой y = 1 , в третьей области — от 0 до параболы. Точки пересечения прямой y = 1 и параболы: (1; 1) и (−1; 1) . В первой точке полярный угол составляет 
, во второй точке он составляет 
. Поэтому в первой области φ меняется от от 0 до , во второй области — от 0 до , в третьей области — от до π .
Запишем линии, ограничивающие область интегрирования в полярной системе координат. Найдём уравнение прямой y = 1 : 
или 
. Найдём уравнение параболы y = x² в полярной системе координат:
Теперь у нас есть всё, чтобы от данного повторного интеграла перейти к полярным координатам:
Пример 3. Вычислить в полярных координатах двойной интеграл
,
где область D ограничена линией окружности 
.
Решение. Строим на чертеже область интегрирования.
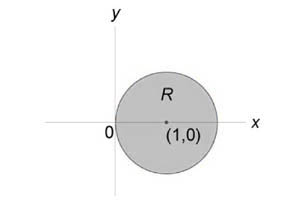
Область интегрирования ограничивает линия окружности с центром в точке (a; 0) и радиусом a . В этом легко убедиться, преобразовав её уравнение следующим образом:
.
Линия окружности касается оси Oy , поэтому полярный угол в области интегрирования меняется от 
до 
. Подставим 
и 
в уравнение окружности и получим
Напишем подынтегральную функцию в полярных координатах:
.
Теперь можем перейти в данном двойном интеграле к полярным координатам:
Наконец, находим двойной интеграл в полярных координатах:
В полученном выражении второе слагаемое равно нулю, так как и sinπ , и sin(−π) равны нулю. Продолжая, получаем:
Пример 4. Вычислить плоской фигуры, которую ограничивают линии 
, 
, 
, 
.
Решение. Построим заданную фигуру на следующем рисунке.
Так как фигура является частью круга, её площадь проще вычислить в полярных координатах. Данные уравнения линий перепишем в полярных координатах:
Таким образом, у нас есть всё, чтобы записать площадь фигуры в виде двойного интеграл в полярных координатах, перейти к повторному интегралу и вычислить его:
Пример 5. Вычислить в полярных координатах двойной интеграл
,
где область D ограничена линиями 
и 
.
Решение. Преобразуем данные уравнения линий, чтобы было проще построить чертёж:
.
Строим на чертеже область интегрирования.
В данных уравнениях линий перейдём к полярным координатам:
.
В данном двойном интеграле перейдём к полярным координатам, затем к повторным интегралам и вычислим интеграл:
Видео:Вычисление двойных интегралов в ПСК (полярной системе координат). Примеры.Скачать
Переход к полярным координатам в двойном интеграле окружность
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |
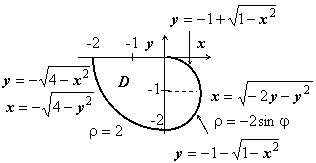Решение:
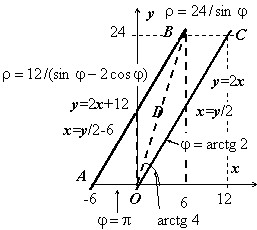$I=intlimits_ ^0 < dxintlimits_0^ > +intlimits_0^6 < dxintlimits_ ^ > +intlimits_6^ < dxintlimits_ ^ > $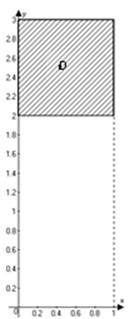
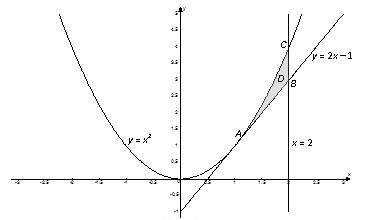
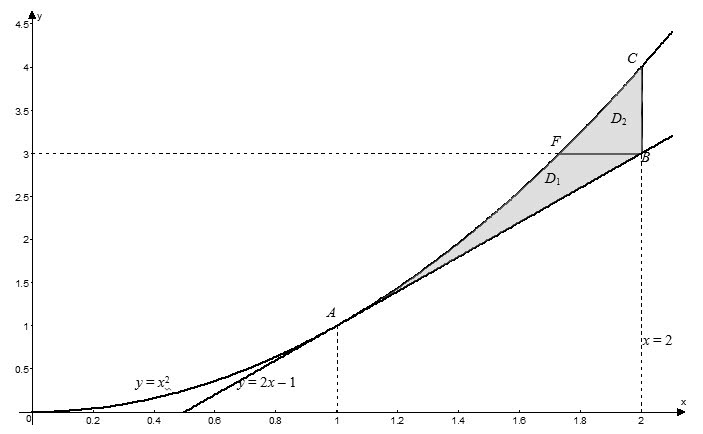
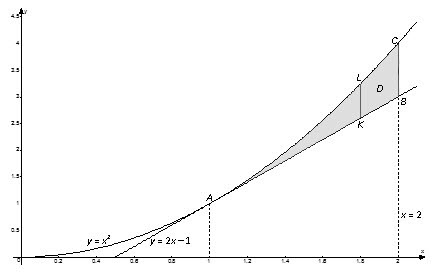Из рисунка в области $D$ видно, что левая граница контура области – одна линия < положительная ветка параболы $y= < ^ > $), а его правая часть состоит из двух линий $AB$ < отрезок прямой $y=2x-1$) и $BC$ < отрезок прямой $x=2$), то есть задается разными уравнениями. В этом случае область $D$ нужно разбить на части так, чтобы каждая из них справа была ограничена только одной линией. В данном случае такими частями будут $ < _ > -ABF$ и $ < _ > -BCF$. Заданная область $D$ будет суммой областей $ < _ > $ и $ < _ > $. Тогда искомый интеграл будет равен сумме интегралов по каждой из областей:
