О волчках,велосипедах,электродвигателе и законе всемирного тяготения.
Разговор о простых физических опытах постепенно перетекает к обсуждению теории поля.
Глава 1.Эксперимент
Речь идет об одном известном и интересном явлении.
Все знают что такое волчок,он же юла, а в технике — гироскоп.
Это тело вращения способное демонстрировать устойчивость. Оно может вращаться в двух
основных позициях :
1.Ось вращения вертикальна, плоскость вращения горизонтальна.юла,волчок
2.Ось вращения горизонтальна,а плоскость вращения вертикальна.колесо велосипеда
С гироскопом и подобными ему дисками вращения, проводились многочисленные опыты
http://tmarh.bizland.com/SENS/98/05-1.html
для получения ответа на один вопрос: происходит ли потеря веса при вращении. Опыты
эти имели целью разгадать тайну летающих дисков и поэтому проводились в позиции 1
Вывод: потеря веса теоретически возможна ,но на таких больших скоростях,что экпериментально это проверить трудно.
В то время как в одной немецкой телепрограмме Nou-xauпоказан любопытный опыт где раскрученный волчок расположен в позиции 2.
Причем волчок имеет только одну точку опоры,второй конец его свободен и зависает в воздухе будто он становится невесом!Это факт не опровергают и физики теоретики,примечание *
но затрудняются объяснить.
Чтобы проверить это провел эксперимент,который легко повторить.
Взял велосипед,перевернул его кверху колесами,поставил седлом на напольные весы весы показали вес 10 кг. и сильно раскрутил заднее колесо.
При максимально больших оборотах весы показали потерю веса до 2-х киллограммов.
Это примерно соответствует весу вращающейся части обода.
При горизонтальном расположении, в позиции 1 вес не меняется,как это и следовало ожидать.
Поскольку глазам своим не верил опыт провел неоднократно,а после то как
факт потери веса вращающегося обода или диска в позиции 2
стал очевидным, начал искать теоретическое объяснение этому-пока без успеха.
Вот и решил эти свои наблюдения и соображения выложить в интернет,может быть
коллективным умом постигнем.
В интернете есть попыткам объяснения этого возникающими завихрениями воздуха.Провел эксперимент примечание ** который эту гипотезу опровергает.
Логическое обоснование. 1 предварительное.
Некогда, некто Галилей, нашел логическое объяснение физического факта независимости времени и скорости падающего тела от его массы,он сделал это до того как подтвердил это свои логические выводы опытом. Попробуем и мы рассуждать здесь логически тем более,
что формулы нам пока никак не помогают
Вращается обод или диск в вертикальной плоскости.
Мы знаем,что масса в этом случае неизменна,а значит и вес вращающегося тела
остается, так как вес тела это сила с которой Земля притягивает тело.
Почему весы показывают отсутствие веса? Потому что весы измеряют давление
колеса на ось вращения,а не вес. А это несколько разные в нашем опыте понятия.
Далее: половину пути движение колеса происходит вверх,а половину — вниз.
Теперь, во первых,при движении вниз, например в состоянии свободного падения, тело
теряет вес или, точнее, не оказывает давление на ось.Это мы знаем,но для примера:
если человек находится в кабине лифта,а лифт свободно падает,то давление
человека на пол стремится к нулю.Так вот при движении обода колеса вниз оно не давит на ось! Но может быть тело при вращении давит на ось двигаясь вверх,
как это происходит при взлете космического корабля,
когда перегрузки растут многократно? Нет.
Как же может тело давить на ось, которая неподвижна,в то время как сила давления
направлена должна быть вниз, а сила инерции движения,
при больших скоростях превосходящая вес, направлена вверх.
Таким образом, и при движении обода колеса вверх и при движении вниз,
давление на ось с увеличением скорости будет стремиться к нулю.
Глава Вторая.Гипотезы.
Можно рассмотреть такие алогичные пока теории в качестве рабочей гипотезы.
Физический смысл происходящего скрыт в таких явлениях как :
А — скорость распространения гравитационных полей и
В — условия взаимодействия гравитационных полей и полей вообще.
Для начала опишем явление известное.
Трехфазный асинхронный электродвигатель имеет статор, где вращается электромагнитное поле
и ротор где тоже есть его собственное наведенное электромагнитное поле.Двигатель работает в нормальном режиме когда скороть вращения поля статора и ротора совпадают,вернее ротор
несколько отстает до 10 %это называется скольжение.
Если отставание растет сцепление полей ротора и статора нарушается и двигатель теряет мощность.Из этого можно сделать предположение:
ДЛЯ ВЗАИМОДЕЙСТВЯ ПОЛЕЙ в том числе гарвитационных НУЖНО ЧТОБЫ ОНИ ДВИГАЛИСЬ С ОДИНАКОВОЙ или близкой ОТНОСИТЕЛЬНОЙ СКОРОСТЬЮ.
Два тела имеют гравитационную массу и гравитационное поле. Чтобы поля двух тел взаимодействовали нужно чтобы тела находились на одинаковом расстоянии друг от друга. Известная формула Закона всемирного тяготения справедлива для состояния покоя.
ПРИ ОТНОСИТЕЛЬНОМ ДВИЖЕНИИ ГРАВИТАЦИОННЫХ МАСС ПРОИСХОДИТ УМЕНЬШЕНИЕ, А БОЛЬШИХ ОТНОСИТЕЛЬНЫХ СКОРОСТЯХ — РАЗРЫВ ГРАВИТАЦИОННОГО ВЗАИМОДЕЙСТВИЯ.
Так же как в случае с электродвигателем.
Это объясняет:
— исчезновение веса при свободном падении.
— вторую космическую скорость,необходимую для преодоления гравитации планеты.
При небольших относительных скоростях гравитационные поля тела и Земли взаимодействие сохраняют,но при больших гравитация исчезает. Если это верно, ТО ТЕЛО БУДЕТ ПАДАТЬ
С УСКОРЕНИЕМ СВОБОДНОГО ПАДЕНИЯ ТОЛЬКО ДО ДОСТИЖЕНИЯ ОПРЕДЕЛЕННОЙ СКОРОСТИ,далее по инерции. Скорость эта в физике называется установившейся или предельной скоростью и пока объясняется пропорционально растущим сопротивлением воздуха.
В нашем случае, когда колесо вращается в горизонтальной плоскости расстояние не меняется и вес остается неизменным.
КОГДА КОЛЕСО ВРАЩАЕТСЯ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ НА БОЛЬШОЙ СКОРОСТИ ВЗАИМОДЕЙСТВИЕ ГРАВИТАЦИОННЫХ ПОЛЕЙ РАЗРЫВАЕТСЯ И ВЕС ПРОПАДАЕТ.
Для проверки версии того, что поля не взамодействуют на больших относительных скоростях придется провести еще один эксперимент может быть не очень убедительный но зато вполне демонстративный:
ЭКСПЕРИМЕНТ 2
Берем магнит. Держим в руке легкий металлический предмет,например ножницы. Проводя
магнитом вблизи ножниц можно пальцами почувствовать действие магнитного поля.Если наловчиться и проводить магнит вблизи ножниц на большой скорости действие поля не чувствуется даже если в руке держать компас.
Глава третья.
И еще одно нечто очень важное: пока физики спорят от том с какой скоростью распространяется гравитационное поле,рассмотрим гипотезу о том что гравитационное поле СТАТИЧНО относительно материнской массы,не имеет скорости распространения и если движется вместе с массой. Есть такие предположения.
Силу гравитации можно представить как энергию,например. потенциальную. Тогда предельно
большая скорость распространения гравитационного поля означала бы истечение энергии , а истечении энергии при таких больших скоростях должно приводить к потере массы.
А этого не происходит. Значит ГРАВИТАЦИОННОЕ ПОЛЕ СТАТИЧНО,
как статична величина массы и потенциальной энергии.
Глава четвертая.
Теперь рассмотрим версию о том что гравитационное поле все-таки движется и верно то что скорость его распространения близка с скорости света.
Но нас интересует не величина а направление.
Если есть скорость должна быть траектория.
Нам показалось странным такое предположение физиков, что направление движения гравитационного поля — от источника. Неясно как такое движение рождает силу притяжения в направлении к источнику?
Предполагаем, что траектория движения или действия гравитационного поля есть замкнутая кривая — круг или эллипс и поле состоит из бесконечно большого числа таких завихрений.Наиболее близкая иллюстративная картина — фонтан.
Так же,например, ядро атома имеет поле и электроны движутся по орбиталям S P d F и G повторяя траекторию гравитационного поля ядра. Так же движутся малые небесные тела по эллиптической орбите вокруг Солнца.Планеты из-за своей массы двигаются по эллипсу близкому к окружности. Все это очень иллюстративно. Во всяком случае реальная картинка мира подтверждает эту гипотезу.Так что гравитационное поле и статично и подвижно одновременно.
Глава пятая. Общие выводы.
Закон всемирного тяготения не отменяется.Во всех случаях тела притягиваются друг другу пропорционально произведению их масс и деленному на квадрат расстояния.
Но в состоянии относительного покоя — при постоянной величине R (радиуса орбиты)
Речь идет о взаимодействии гравитационных полей двух тел,которые движутся относительно друг друга то есть приближаются или отдаляются,потому как тяготение передается через гравитационное поле. А поля двух тел, как мы это сначала предположили, а потом выяснили,имеют свойство терять свое взаимодействие при своих смещениях то есть при относительной скорости тел.
Под относительной скорости тел мы здесь понимаем ситуацию, когда одно тело условно неподвижно, а другое перемещается по линии соединяющей центры их гравитационных масс.Орбитальное,касательное или горизонтальные движения не рассматриваются.Только радиальное движение.
В качестве рабочей можно вывести формулу :
Vt — Vo
Fо = F х ———
Vt
где: Fо — сила действия гравитации при движении со скоростью Vo
F — сила гравитации в состоянии покоя при постоянстве R
Vo — относительная скорость
Vt — установившаяся скорость или скорость при которой гравитяционные поля теряют взаимодействия. Около 40 мсек
Из формулы видно: При Vo равной нулю сила гравитации максимальна.
При Vo равной Vt сила гравитации равна нулю.
Для проверки некоторых версий провел
ЭКСПЕРИМЕНТ 3
В колесо велосипеда как в эксперименте 1 налил воду с тем чтобы увеличить его массу. Раскрутил колесо. Вес до вращения колеса -12 кг. при вращении колеса в вертикальной плоскости на максимальных оборотах вес падает до 7 кг. Таким образом падение веса при вращении пропоционально массе и зависит только от не и не является следствие воздушных завихрений.
Примечание 3. Пока известен только один один эксперимент по измерению скорости распространения гравитационного поля:
http://www.atheism.ru/science/science.phtml?id=814
В заключении.
Автор пока утратил интерес к этой теме. В силу невозможности поставить чистый эксперимент. причина «исчезновения веса» верноятно кроется в том что велосипедное колесо — эксцентрик и подпрыгивал на пружинных весах.
Продолжение за 28.12.2014.
Сегодня по каналу «Дискавери» показали интересный видеосюжет.
В Сиднее (Австралия) провели опыты с вращающимся диском.
Диск весом в 19 кг. поместили на подшипники на конце стержня (как на штанге)
Второй конец был свободен и атлет пытался поднять конструкцию рукой за свободный конец стержня.
Это ему не удавалось.
Затем диск с помощью электродрели раскрутили и диск оказалось можно свободно поднять за один конец и даже над головой.
Анализ и вывод. Мы делаем однозначный вывод, что диск при вращении сильно потерял в весе. Условием для этого является круговое движение диска с большой скоростью в вертикальной плоскости.
PS Информация для тех кто хочет перевернуть мир своими теориями:
http://www.astrogalaxy.ru/624.html
http://garshin.ru/evolution/heuristics/patent.html
Глава шестая от 12.07.16.
Видео опыта с колесом :
https://www.youtube.com/watch?v=VDNnz3xcwj0#t=63.483229
Видео. Эксперимент — отклик на эту статью. Автор Игорь Белецкий
https://www.youtube.com/watch?v=2oOtpIhiNdQ
Спасибо автору ролика, который поставил этот эксперимент. Но в чем его недостоверность? Похоже автор ставил целью разоблачение и поставил опыт именно так. Он может легко установить весы в любое положение, добавив груз на одну сторону.
И на разоблачающем опыте, он сначала удерживает руками весы, а потом раскручивает
гироскоп и отпускает руку. Шутник. Это легко сделать, если сначала отрегулировать весы с учетом потери веса. И там видно, что на повторном опыте одного болтика на левой стороне нет и колесо показывается только с торца, когда вращения не видно.
Видео надо было довести до полной остановки колеса и показать, что весы при этом останутся в равновесном состоянии.
И потерю веса надо фиксировать на точных весах. со шкалой.
Кроме того, велосипедное колесо имеет большой диаметр. И маленькое колесо — эффекта не показывает. По тому как, известно, что все эффекты во вращающихся колесах находятся в квадратной зависимости от радиуса вращения.
Диаметр колеса велосипеда — 600 см. — в пять раз больше.
Кроме, того, его колесо, по видимому, алюминиевое и легкое. И вес его внешней части будет всего граммов 200 и уловить его потерю на таких весах не получиться.
Удельный вес алюминия всего — 2.7 грамма на куб. сантиметр.
делаем расчет. При диаметре колеса 6 см. длина обода — 2 х 3.14 х 6 = всего 37.6 см.
При ширине обода 1 см толщине 2 см и объеме 75.2 кв. см. и вес 75.2 х 2.7 = всего 203. грамма.
Вывод. Опыт проведенный Игорем Белецким поставлен некорректно.
1. Если проводить опыты, то с колесом большой массы и диаметра и с большими скоростями.
2. Прежде чем искать обоснования или опровержения, надо определиться со скоростью поля гравитации, взаимодействием полей при скоростях и торсионными полями — тороидальная энергия.
Глава седьмая. от 15.12.16.
Мне прислали ссылку https://www.youtube.com/watch?v=H_hRkwveBZY
из НИАУ МИФИ Подвешенный волчок.
На ролике видно как профессор ставит опыт с вращающимся диском.
Диск вращается в вертикальной плоскости, это важно.
Во второй части опыта диск раскручивается сильнее и он поднимается вверх!
У него появляется подъемная сила! Не только исчезает вес но диск поднимается вверх.
Этот опыт окончательно подтверждает наше предположение о том, что диск, который вращается с большой скоростью в вертикальной плоскости — теряет в весе и даже приобретает подъемную силу.
Глава восьмая. от 16.12.16.
Когда массивное тело вращается с большой скоростью, возникают так называемые торсионные поля. Они перекрывают,экранируют, поля гравитации.
Когда вращение происходит в вертикальной плоскости (колесо велосипеда)
то направление торсионным полей и полей гравитации происходит по одной линии и это приводит к потере веса.
Когда торсионные поля возникают в горизонтальной плоскости (юла, волчок)
поля гравитации перекрываются (потому волчок не падает) но исчезновение веса не происходит.
Ещё можно и так сказать: если поле гравитации действует на массу, то тогда и масса действует на поле гравитации. И когда большая масса вращается с большой скоростью, поле гравитации отбрасывается от тела центробежной силой и на тело не действует.
примечание *
Беркелевский курс физики том 1 авт.Ч.Китель У.Найт М.Рудерман :Москва 1975 г
издательство «Наука»
8.5. . В дальнейшем мы придем к поразительному выводу о том,что волчок будет
устойчив,когда ось его расположена горизонтально.
Последние замечания от 21.07.18.
В интернете появилось много роликов с диском, вращающимся в вертикальной плоскости. И заметно следующее:
1. Диск становится явно легче и это чувствуется при подъеме рукой. Но весы падение веса могут не показывать. Почему?
По тому как исчезновение веса действует только на диск, а весы показывают давление стойки, на которой крутится диск. И это давление — не меняется.
Так как сила, возникающая при вращении диска, с одной стороны действует на диск — облегчая его, а другой — на опору.
Соображение от 31.01.20.
См. фото. Вращение колеса происходит в плоскости действия силы гравитации.
Это приводит к возникновению силы, поднимающей тело (колесо) вверх.
Это видно на фото, где свободная часть оси — поднимается.
Эта сила одной стороной действует на опору, а другой — поднимает колесо.
По этому, проводившие эксперимент сообщают о том, что весы не показывают падения веса, при том, что колесо задирает вверх и его тяжелое — легко поднять.
Это примерно так же, как если бы мы, стоя на весах, поднимали вверх груз.
- Перегрузка тела при движении по окружности
- § 32. Кинетозы
- § 33. Перегрузка
- § 34. Невесомость
- Расчет перегрузки при движении по окружности
- Движение по окружности
- Угловая скорость
- Нормальное ускорение
- Тангенциальное ускорение
- I. Механика
- Тестирование онлайн
- Угловая скорость
- Период и частота
- Линейная скорость
- Центростремительное ускорение
- Вращение Земли
- Связь со вторым законом Ньютона
- Как вывести формулу центростремительного ускорения
- Движение по циклоиде*
- Движение по окружности
- Скорость при движении по окружности
- Ускорение материальной точки при движении по окружности
- Период и частота — характеристики равномерного движения по окружности
- Примеры задач с решением
Видео:Физика - движение по окружностиСкачать

Перегрузка тела при движении по окружности
Часть первая. ОБЩАЯ НОЗОЛОГИЯ
Раздел III. БОЛЕЗНЕТВОРНЫЕ ДЕЙСТВИЯ ФАКТОРОВ ВНЕШНЕЙ СРЕДЫ
Глава 2. Повреждающее действие ускорений и невесомости на организм
В связи с развитием скоростных видов транспорта, аэронавтики и космонавтики человек стал подвергаться значительным ускорениям или же испытывать состояние невесомости. При определенных условиях оба этих фактора могут вызвать заметные нарушения функций организма.
§ 32. Кинетозы
Кинетоз — болезнь передвижения (от греч. kynesis — движение) возникает при действии на организм более или менее продолжительных и изменяющихся ускорений. Существуют и другие названия кинетозов: укачивание, морская болезнь, воздушная болезнь, автомобильная болезнь и др.
Для кинетозов характерны нарушения координации движений, головокружение, тошнота, рвота, бледность, холодный пот, снижение артериального давления, урежение сердечных сокращений. В тяжелых случаях возможно депрессивное состояние, астения, нарушения ясности сознания. Однако после прекращения действия ускорений симптомы кинетозов исчезают.
Причинами кинетозов могут быть следующие виды ускорений и их сочетания:
- прямолинейное (положительное или отрицательное) ускорение, например при прямолинейном движении в поезде, автомобиле, подъемах или спусках в лифте и т. д.;
- радиальное или центростремительное ускорение, например при воспроизведении виражей в самолетах, пикировании, вращении в центрифуге и т. п.;
- угловое ускорение, возникающее при неравномерном движении тела по окружности;
- ускорение Кориолиса, которое возникает, когда тело, движущееся с равномерной угловой скоростью по окружности или ее отрезку, одновременно приближается к центру вращения или удаляется от него.
Последние две формы ускорений имеют особое значение при полетах в космических кораблях и могут стать причиной космического укачивания.
В наземных условиях (поездка в автомобиле, поезде и пр.) на организм человека обычно действуют прямолинейные и радиальные ускорения, непревышающие 1-2g (lg = 9,8 м/с 2 ), оказывающие болезнетворное действие в основном рефлекторно через следующие рецепторы:
- рецепторы вестибулярного аппарата, которые являются наиболее специфическими и чувствительными к восприятию ускорений. Пороговая величина раздражения вестибулярных рецепторов равна 0,01 g. Причем механорецепторы отолитового аппарата воспринимают преимущественно прямолинейные ускорения, рецепторы полукружных каналов — угловые ускорения;
- проприорецепторы (мышц, связок, сухожилий) и механорецепторы кожи и внутренних органов раздражаются от смещения тела, изменения тонуса мышц и т. д.;
- зрительные рецепторы раздражаются от быстрых смещений пространственных ориентиров — горизонта, облаков, мелькания близких предметов — деревья, дома и пр;
- рецепторы слизистых и серозных оболочек органов брюшной полости раздражаются при смещении внутренних органов, натяжении и смещении брюшины, брыжейки и пр.
В патогенезе кинетозов решающее значение имеет влияние ускорений на вестибулярный и зрительный анализаторы (схема 3).
Сильное раздражение рецепторного аппарата вестибулярного нерва по чувствительным путям направляется в ретикулярную формацию и вестибулярные ядра в ромбовидной ямке. Отсюда через веревчатое тело импульсы поступают в мозжечок. Благодаря тому, что во время укачивания раздражаются попеременно разные рецепторы вестибулярного аппарата, мозжечок получает импульсы, вызывающие изменения тонуса различных групп мышц шеи, спины, конечностей — отсюда асимметрия тонуса мышц, нарушения координации движений.
Вегетативные расстройства при кинетозах зависят от возбуждения ядер вегетативных нервов. Из вестибулярных ядер импульсы передаются на чувствительные и двигательные ядра блуждающего нерва, что вызывает снижение артериального давления, брадикардию, тошноту и рвоту, отделение пота. Указанные вегетативные рефлексы поддерживаются также раздражением интерорецепторов внутренних органов, в особенности желудка.
Через ретикулярную формацию импульсы вестибулярного нерва достигают гипоталамуса и способствуют возбуждению симпатического отдела вегетативной нервной системы. Известно, что медиальная преоптическая зона и медиальный гипоталамус (симпатическая область) тесно взаимосвязаны с вестибулярными ядрами. От активации симпатической системы зависят такие симптомы, как атония, угнетение перистальтики кишечника, побледнение.
Проявления кинетозов более выражены у лиц с повышенной возбудимостью симпатического или парасимпатического отделов нервной системы или вестибулярного анализатора.
§ 33. Перегрузка
При действии на тело ускорений возникают силы инерции, направление которых всегда противоположно направлению ускорения. В медицине и биологии для обозначения этих сил применяют термин «перегрузка».
Перегрузка (η) — отношение силы (F), действующей на тело человека, к массе его тела (m): η = F/m
Перегрузка не имеет размерности и выражается относительными единицами, показывающими во сколько раз увеличилась масса тела при данном ускорении по сравнению с обычной земной гравитацией. Направление сил инерции — вектор перегрузки — всегда противоположно направлению ускорения.
В зависимости от направления вектора перегрузки по отношению к вертикальной оси тела перегрузки делят на продольные и поперечные.
Продольные перегрузки бывают:
- положительные — вектор перегрузки от головы к ногам (направление ускорения при этом от ног к голове, например, при подъеме в лифте);
- отрицательная продольная перегрузка — вектор перегрузки от ног к голове (направление ускорения- от головы к ногам, например, при спуске в лифте);
- поперечные перегрузки — вектор перегрузки спина — грудь или грудь — спина;
- боковые перегрузки вектор перегрузки бок-бок.
Направление перегрузки имеет важные последствия для организма. Наибольшие повреждения при наименьшем времени действия оказывают на организм человека продольные отрицательные перегрузки.
Перегрузки, возникающие в наземных условиях, как правило, не велики и не вызывают существенных повреждений в организме человека. И только с развитием скоростной авиации и космических кораблей возникла проблема переносимости организмом человека значительных ускорений и перегрузок. Как видно из табл. 4, человек сохраняет работоспособность при больших перегрузках в течение немногих секунд и минут.
В табл. 4 приведены сведения о переносимости перегрузок тренированными пилотами. Основным критерием для оценки состояния пилота взяты изменения работоспособности. Для нетренированных лиц пределы переносимости перегрузок значительно ниже.
| Таблица 4. Переносимость перегрузок человеком (Комендантов Г. Л., 1975) | ||||
| Направление ускорения | Направление вектора перегрузки | Величина перегрузки | Время действия перегрузки (секунды) | Состояние пилота |
| От ног к голове (взлет) | Голова — ноги (положительная перегрузка) | 5-6 | ||
Более 9
Не более 20
Нарушение зрения, серая пелена, возможен обморок.
Обморок, опасно для жизни
5-6
0,2-0,5
Опасно для жизни
Возможно при катапультировании вниз
До 26
Не более 8
Деформация тканей, петехиальные кровоизлияния
Более 14
Менее 20
Деформация тканей, разрывы сосудов склеры
Общее состояние человека при перегрузках характеризуется появлением чувства тяжести во всем теле, болевых ощущений, вначале затруднением, а в дальнейшем и полным отсутствием возможности произвольных движений. Происходит смещение мягких тканей и ряда внутренних органов в направлении действия перегрузки. Для перегрузок, направленных от головы к ногам, характерны зрительные нарушения — затуманивание и ослабление периферического зрения — «серая пелена», далее ослабление и даже потеря центрального зрения, так называемая «черная пелена». Эти расстройства обусловлены нарушениями гемодинамики мозга и сетчатки глаза. Перегрузки, направленные от ног к голове, вызывают очень сильные болевые ощущения в голове и глазах, возможны кровоизлияния в склеру и веки. Для поперечных перегрузок характерны затруднения дыхания вплоть до невозможности сделать вдох, появляются болевые ощущения в эпигастральной области.
В механизме расстройств функций организма при перегрузках ведущую роль играют нарушения гемодинамики и дыхания.
Нарушения гемодинамики обусловлены главным образом перераспределением крови. При положительных перегрузках (голова-ноги) происходит перемещение крови в сосуды брюшной полости и нижние конечности. В результате такого перераспределения артериальное давление в сосудах, расположенных ниже уровня сердца, повышается, а ударный объем сердца уменьшается. В сосудах верхней половины туловища давление падает. Возникающая при этом анемия мозга и органов чувств может привести к расстройствам зрения и потере сознания.
При перегрузках от ног к голове (отрицательные перегрузки) перемещение крови происходит к сосудам верхней половины туловища, артериальное давление выше уровня сердца резко повышается.
Изменения общей гемодинамики при поперечных перегрузках выражены значительно меньше, чем при продольных, что обусловлено расположением магистральных кровеносных сосудов вдоль продольной оси тела. Однако во многих органах и тканях микроциркуляторное ложе может быть распределено более или менее равномерно по всем направлениям, и поэтому возможны регионарные смещения крови и при поперечных перегрузках, например в системе легочных сосудов — спереди назад.
Нарушения дыхания и газообмена также зависят от направления перегрузки. При положительных продольных перегрузках легочная вентиляция увеличивается — возрастают и глубина дыхания, и частота дыхательных движений. Увеличение дыхательного объема, по-видимому, зависит от опущения диафрагмы. Минутный объем дыхания (МОД) возрастает иногда более чем в 3 раза, возрастают потребление кислорода и выделение СO2, увеличивается дыхательный коэффициент. Однако, несмотря на увеличение МОД и дыхательного объема, постепенно нарастает гипоксия вследствие выраженного нарушения гемодинамики в сосудах легких.
Так, известно, что при 6-7-кратных перегрузках кровоток в верхних долях легких прекращается, в средних частях не изменяется, а в нижних долях возникают отеки и ателектазы.
Наиболее значительные расстройства дыхания возникают при поперечно направленных перегрузках, что обусловлено сочетанными нарушениями биомеханики дыхательного акта и кровообращения в сосудах малого круга кровообращения. Осуществление нормального дыхательного акта затруднено. Наблюдается учащение дыхания, удлинение фазы вдоха и укорочение выдоха и постепенное снижение его глубины. Жизненная емкость легких с возрастанием перегрузок снижается.
Нарушения функции дыхания и гемодинамические расстройства ведут к гипоксемии и гипоксии всех органов и тканей, прежде всего головного мозга и сердца. На этом фоне имеет существенное значение измененный поток афферентной импульсации как от внешних, так и от внутренних рецепторов организма. Необычная импульсация наряду с гипоксией мозга способствует нарушениям механизмов центральной регуляции жизненно важных функций организма и снижению компенсаторно-приспособительных возможностей организма. От больших перегрузок может наступить острая смерть вследствие сердечной, сосудистой или дыхательной недостаточности.
§ 34. Невесомость
Состояние невесомости человек испытывает только при космических полетах (если не считать очень кратковременных периодов невесомости, искусственно создаваемых в наземных условиях).
Невесомость — это состояние, когда на тело человека не действует сила тяжести или эквивалентные ей инерционные силы. В невесомости масса тела равна 0. Однако механические воздействия, исходящие из самого организма, в известной мере сохраняются. Так механические воздействия, оказываемые на механорецепторы сосудов и тканей, уменьшаются, но не исчезают полностью, остаются механические процессы, связанные с деятельностью сердца, сосудов, дыхательных мышц, проявления выпрямительных установочных рефлексов и др.
Болезнетворное действие невесомости на организм несравненно меньше, чем таковое перегрузок.
В состоянии невесомости в организме возникают сенсорные, двигательные и вегетативные изменения.
Сенсорные изменения проявляются в нарушении или затруднении ориентации — возникает ощущение крена, «перевернутости», головокружение и пр. Возникновение этих реакций связано с измененной афферентацией с рецепторных зон ряда анализаторов: проприоцептивных, вестибулярных, кожных и др. Нарушение функциональной системности в работе анализаторов, ослабление в условиях невесомости реципрокных влияний с отолитового аппарата на функции полукружных каналов и, возможно, влияние ускорений Кориолиса могут вызвать космическую форму укачивания с сенсорными и вегетативными расстройствами, схожими с таковыми при укачивании в наземных условиях.
Вегетативные расстройства в условиях невесомости довольно выражены. Характерна большая изменчивость физиологических показателей. Артериальное давление неустойчиво, чаще снижено. Со стороны сердца вначале наблюдается тахикардия, а в более поздние периоды брадикардия, по-видимому, в силу функционального приспособления сердца к уменьшению механической нагрузки. Дыхание, вначале несколько учащенное, быстро нормализуется, а в дальнейшем замедляется. Функции пищеварительных органов существенно не меняются. После длительного пребывания в невесомости значительно уменьшается масса тела, главным образом за счет потери воды (усиление диуреза). Усиление выделения воды и ионов натрия зависит, по-видимому, от изменений в сердечно-сосудистой системе. Так как в невесомости исчезает гидростатическое давление крови в сосудах, нивелируется и имеющаяся в наземных условиях разница давления крови в сосудах верхней и нижней половинах туловища (на земле давление крови в ступнях ног примерно на 100 мм рт. ст. выше, а в сосудах мозга на 30-40 мм рт. ст. ниже, чем на уровне сердца). Из-за потери гидростатического давления кровь в невесомости распределяется равномерно во всех сосудистых областях, следовательно, кровенаполнение верхней половины туловища становится больше, чем в наземных условиях. Переполнение предсердий кровью и растяжение их угнетает рефлекторно продукцию антидиуретического гормона (рефлекс Генри-Гауэра), что приводит к увеличению мочеотделения, потере натрия, дегидратации и уменьшению объема циркулирующей крови.
Длительное состояние невесомости сопровождается усиленным выведением кальция из организма. За 7-8 нед пребывания в невесомости содержание кальция в костях может уменьшится на 5-7%. Наиболее интенсивное рассасывание кальция происходит в трабекулярных, бедренных костях, костях голени, в телах позвонков, в пяточной кости — в участках наиболее интенсивного обмена.
Двигательные изменения в невесомости выражены не столь резко. Работоспособность космонавтов в общем сохраняется, хотя точность движений может несколько снижаться. Чаще нарушаются тонкие координационные акты. Несколько уменьшается мышечная сила рук.
Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Расчет перегрузки при движении по окружности
Видео:Вес тела. Невесомость и перегрузки. 10 класс.Скачать

Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Видео:Урок 89. Движение по окружности (ч.1)Скачать

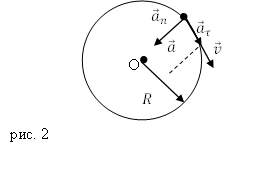
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Видео:КАК ЗА 6 МИНУТ понять физику? Вес тела, Перегрузка и НевесомостьСкачать

I. Механика
Видео:Центростремительное ускорение. 9 класс.Скачать

Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Видео:Движение тел по окружностиСкачать

Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Видео:Ускорение при равномерном движении по окружностиСкачать

Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Видео:Физика | Равномерное движение по окружностиСкачать

Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Видео:Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Видео:Урок 62. Сила тяжести и вес тела. Невесомость.Скачать

Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть 

Видео:Урок 63. Перегрузка. Вес тела на полюсе и на экватореСкачать

Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью 
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Видео:Вес тела (ускорение направлено вверх), перегрузкаСкачать

Движение по окружности
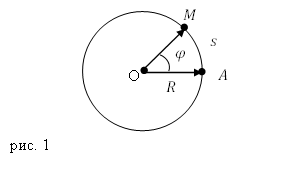
Значимым частным случаем перемещения материальной точки по заданной траектории служит движение по окружности. Местоположение точки на окружности можно задавать не при помощи расстояния от некоторой начальной точки (допустим A), а с помощью угла $varphi $, который образуют радиусы, которые провели из центра окружности (O) к рассматриваемой частице (точка M) и из О в точку начала отсчета (A) (рис.1).
Видео:Вращательное движение. 10 класс.Скачать

Скорость при движении по окружности
При движении по окружности вместе со скоростью движения по траектории ($v$- линейная скорость) вводят угловую скорость ($omega $), которая характеризует быстроту изменения угла $varphi $:
Определим, какова связь между линейной и угловой скоростями. Длину дуги АМ ($s$) (рис.1) можно найти как:
тогда изменение длины дуги за время$ Delta t$ равно$ Delta s$:
[Delta s=RDelta varphi left(3right).]
Найдем отношение $frac $, разделив обе части выражения (3) на $Delta t$:
Перейдем к пределу в правой и левой частях равенства (4) при $Delta tto 0$, получим:
Видео:Формулы механики 2, движение по окружности, центростремительное ускорениеСкачать

Ускорение материальной точки при движении по окружности
Величина нормальной (центростремительной) компоненты ускорения вычисляется при помощи формулы:
При равномерном перемещении по окружности величина центростремительного ускорения постоянна ($a_n=const). $Угловая скорость при равномерном движении по окружности является постоянной величиной, в этом случае ее называют циклической частотой.
Тангенциальное ускорение при движении по окружности вычисляют, как и при любом криволинейном движении:
Видео:Физика 9 класс. §18 Движение тела по окружности с постоянной по модулю скоростьюСкачать

Период и частота — характеристики равномерного движения по окружности
Равномерное движение по окружности можно характеризовать при помощи такой физической величины как период обращения ($T$), который определяют как время совершения материальной точкой полного оборота. Используют и частоту ($nu$) обращения, которую определяют как величину обратную периоду, равную количеству оборотов за единицу времени:
При равномерном движении по окружности угловая скорость, частота и период связаны как:
Формула (9) дает возможность центростремительное ускорение определить как:
Отметим, что при неравномерном движении по окружности период ($T$) и частота ($nu$) свой смысл теряют, о них можно говорить только при равномерном движении по окружности.
Примеры задач с решением
Задание. Центростремительное ускорение материальной точки, перемещающейся по окружности, имеющей радиус R, задано уравнением: $a_n=A+Bt+Ct^2(frac )$. Каково тангенциальное ускорение точки? Как направлены ускорения точки?
Решение. Сделаем рисунок.
Нормальное ускорение материальной точки, движущейся по окружности можно найти как:
Следовательно, скорость точки:
Используя заданный в условии задачи закон изменения нормального ускорения $a_n=A+Bt+Ct^2(frac )$, выражение (1.3) преобразуем к виду:
Величина тангенциального ускорения определена как:
Подставим правую часть выражения (1.4) в уравнение (1.5), имеем:
Задание. Чему равен путь (s), который проходит точка в примере 1 за время $t_1$, если A= 1 $frac $, $B=6 frac $; $С=9frac $.
Решение. Путь, пройденный точкой можно найти как:
Используем выражение для величины скорости, которое мы получили в первом примере:
Подставим известные нам из условия задачи коэффициенты, преобразуем полученное выражение $v left(tright):$
Вычислим интеграл (2.1), принимая во внимание выражение (2.3):
Ответ. $s=sqrt left(t_1+frac ^2right)$