Паркет из треугольников геометрия

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Геометрические паркеты

Паркет (или мозаика) — бесконечное семейство многоугольников, покрывающее плоскость без просветов и двойных покрытий. Иногда паркетом называют покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек; но мы будем рассматривать как правильные, так и неправильные многоугольники. Итак, какими же многоугольниками можно замостить плоскость?

Паркеты из одинаковых правильных многоугольников

Сумма всех углов n-угольника равна 180°(n-2). Все углы правильного многоугольника равны; следовательно, каждый из них равен 180°(n-2)/n. В каждой вершине паркета сходится целое число углов; поэтому число 2·180° должно быть целым кратным числа 180°(n-2)/n. Преобразуем отношение этих чисел:

Разность n-2 может принимать лишь значения 1, 2 или 4; поэтому n может быть равно только 3, 4 или 6. Значит, можно получить паркеты, составленные из правильных треугольников, квадратов или правильных шестиугольников.

Паркеты из разных правильных многоугольников

Сначала выясним, какое количество различных правильных многоугольников (с одинаковыми длинами сторон) может находиться вокруг каждой точки. Величина угла правильного многоугольника должна находиться в интервале от 60° до 180° (не включая); следовательно, число многоугольников, находящихся в окрестности точки, должно быть больше 2 (360°/180°) и не может превышать 6 (360°/60°).

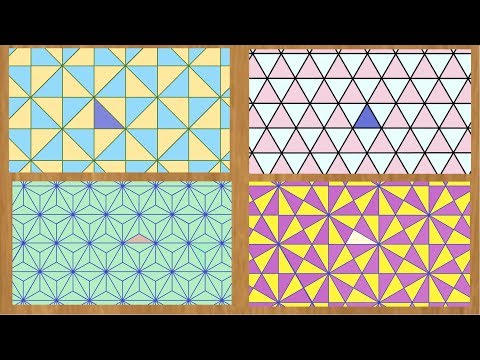
Можно показать, что существуют следующие способы уложить паркет комбинациями правильных многоугольников: (3,12,12); (4,6,12); (6,6,6); (3,3,6,6) — два варианта паркета; (3,4,4,6) — четыре варианта; (3,3,3,4,4) — четыре варианта; (3,3,3,3,6); (3,3,3,3,3,3) (цифры в скобках — обозначения многоугольников, сходящихся в каждой вершине: 3 — правильный треугольник, 4 — квадрат, 6 — правильный шестиугольник, 12 — правильный двенадцатиугольник). Некоторые варианты паркета показаны на следующих иллюстрациях:

Остальные варианты паркетов, а также доказательство того, что не существует других вариантов укладки паркета из правильных многоугольников (при условии, что любые два многоугольника в паркете имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек), см. в статье и др. «Геометрический паркет на экране компьютера» (статья — в виде картинок на двух страницах, объем каждой страницы порядка 500 кб; источник — журнал «Информатика и образование, №9 за 2002 г.).

Паркеты из неправильных многоугольников

Легко покрыть плоскость параллелограммами:

Вообще можно замостить плоскость копиями произвольного четырехугольника, необязательно выпуклого:

Можно составить паркет из копий произвольного треугольника: из двух равных треугольников можно сложить параллелограмм, и покрыть плоскость копиями этого параллелограмма.

Еще плоскость можно покрыть копиями центрально-симметричного шестиугольника, или копиями пятиугольника с двумя параллельными сторонами. До сих пор не найдены все типы выпуклых пятиугольников, из которых складываются паркеты. Зато доказана теорема, утверждающая: «Нельзя сложить паркет из копий выпуклого семиугольника». В то же время существуют паркеты из невыпуклых семиугольников:

Паркеты из произвольных фигур

Некоторые определения паркета не ограничиваются многоугольниками; в этом случае паркетом называется покрытие плоскости без пропусков и перекрытий заданными фигурами (в частном случае — многоугольниками, правильными или неправильными, выпуклыми или невыпуклыми). В таком случае даже для паркетов из многоугольников может не соблюдаться требование «два многоугольника должны иметь общую вершину, общую сторону или совсем не иметь общих точек»; кроме того, появляется множество разнообразных паркетов, состоящих не из многоугольников, а из криволинейных фигур. Рассмотрим способы построения нового паркета, исходя из этого «расширенного» определения. Итак, как нарисовать паркет? (некоторые из возможных способов)

Способ первый. Берем некоторую сетку (уже известный нам паркет) — из правильных треугольников, шестиугольников, квадратов, или из произвольных многоугольников, и выполняем преобразования: сжатие/растяжение, замена прямолинейных отрезков кривыми с началом и концом в тех же точках, что и у отрезков.
Пример: паркеты, полученные заменой отрезков «квадратной» сетки некоторыми кривыми или ломаными.

Способ второй. Объединяем отдельные элементы уже существующих паркетов. Примеры: паркеты, полученные в результате объединения элементов квадратной сетки:

Паркет, каждый элемент которого получен в результате объединения пяти правильных треугольников:

Способ третий. Берем существующую сетку и дополняем ее новыми линиями. Получаем разбиение плоскости на фигуры, которые затем можно по-новому объединить. В частном случае — накладываем друг на друга две (или более) сетки уже известных паркетов, смещая или поворачивая одну сетку относительно другой; фигуры, образовавшиеся при пересечении линий, считаем элементами паркета.
Пример (разбиения сетки из греческих крестов):

Способ четвертый. Выбираем некоторую кривую или ломаную и начинаем ее переносить на некоторый вектор, поворачивать, отражать. получившиеся кривые или ломаные размещаем на плоскости таким образом, чтобы они образовали замкнутые контуры (которые в дальнейшем будут рассматриваться как элементы паркета). Если рассматривать только незамкнутые кривые и ломаные, паркеты будут напоминать полученные способом №1.
Для получения следующего паркета была взята дуга спирали, три раза повернута на 90°, а затем к получившейся фигуре был применен параллельный перенос.

А вот паркеты, полученные с помощью параллельного переноса звездчатых многоугольников:

Совмещая вершины звездчатых многоугольников, получаем паркеты, состоящие из правильных восьмиугольников, равнобедренных прямоугольных треугольников, а также из невыпуклых 16-угольников, напоминающих крест. На первом рисунке есть еще один элемент — выпуклый четырехугольник.

Источники:
. Паркеты из правильных многоугольников. Журнал «Квант» №3, 1970 г. . Паркеты. , , . Геометрический паркет на экране компьютера. Журнал «Информатика и образование», 9-2002.

Также при подготовке страницы были использованы материалы, подготовленные мной для УМК «Геометрические паркеты» («Как нарисовать паркет, или почему не бывает тетрадей в кружочек»).

См. также: Одиннадцать правильных паркетов на сайте Арбуз

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Исследовательская работа по математике » Геометрические паркеты»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Паркеты с древних времен привлекали к себе внимание людей. Паркеты являются своеобразными орнаментами. Над созданием паркетов – орнаментов трудились многие поколения мастеров, подчас создавая истинные шедевры красоты.

Тема «Паркеты» актуальна и в наши дни. Паркетами покрывают полы в домах, укра­шают стены комнат и зданий Каждому из нас хочется, чтобы было не только прочно, но оригинально и красиво, поэтому без многоугольников ни один дизайнер не обойдется, ни один человек, который собирается сделать ремонт.

С паркетами мы встречаемся в повседневной жизни. Тетрадный лист в клеточку представляет собой простейший паркет. Элементом паркета здесь является квадрат. Можно придумать сотни, тысячи разных элементов паркета.

В моей работе я буду рассматривать геометрические паркеты из многоугольников.

Цель и задачи проектной работы.

1.Расширение теоретической базы, аналитический обзор литературы по теме.

2.Изучить геометрические приёмы составления паркетов.

3. Научиться строить паркеты с помощью графического редактора « Paint », входящего в стандартный пакет Microsoft Office .

4.Развитие умений и навыков исследовательской работы.

Выдвинута проблема. Какими правильными многоугольниками можно замостить плоскость?

Объект исследования — паркеты.

Методы исследования: анализ литературы; систематизация материала; метод аналогии.

При работе над проектом я пользовалась материалом из книг, журналов, использовала Интернет — ресурсы.

1. Историческая справка.

Слово «паркет» имеет благородное французское происхождение. Однако в средние века во Франции им обозначали небольшой парк, немного спустя — предназначенную для аудиенций часть зала, покрытую ковром. Ковры постепенно исчезли, паркетные полы стали частью интерьера, так же искусно выполненной, как настенные гобелены.

Русский паркет, насчитывающий несколько сот лет своего существования и имевший самые разнообразные формы, прошел длительный путь своего развития. В России паркетные полы были нововведением Петра I., который привез целый цех краснодеревщиков с Запада, в частности, из Германии. Полы в русских постройках, начиная со времен Петра, приобрели иной, художественный, вид. Ассортимент деревьев, употребляемых для паркета, увеличивался, и наряду с местными отечественными породами: березой, орехом, сосной, лиственницей, кленом, дубом, буком, грабом, ясенем, вязом, грушей, яблоней, ольхой, можжевельником, карагачем и кизилем — стали все более и более применять редкие и дорогостоящие сорта привозных «заморских» деревьев. В зависимости от употребляемых материалов паркеты носили различные названия: цветные (т. е. набранные из привозных деревьев), полуцветные, штучные (набранные из местных пород) и дубовые.

Сейчас, в начале ХХI века, несмотря на развитие науки и техники, можно сомневаться — все ли технологические тайны старых мастеров-паркетчиков удалось восстановить. Можно сказать, что благодаря буквально нескольким мастерам — реставраторам искусство художественного паркета в нашей стране сохранилось до наших дней.

Паркет в Итальянском зале Паркет начала 18 века

Правда, технология со временем изменяется, детали орнамента и рисунка сегодня вырезаются уже не вручную, а на станках и с применением лазера и компьютера, появилось много машин, облегчающих труд.

2. Геометрические п аркеты.

П аркетом называют замощение плоскости многоугольниками, при котором вся плоскость оказывается покрытой ими без просветов и двойных покрытий. Иногда паркетом называют покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину, либо совсем не имеют общих точек.

2.1. Паркеты из правильных одноименных многоугольников.

1.Из каких правильных одноименных многоугольников можно составить паркет?

Предположение: правильные паркеты получатся из квадратов, шестиугольников и треугольников.

В природе и в жизни человека паркеты встречаются часто. Например: шахматная доска и пчелиные соты. Все эти предметы состоят из многоугольников с равными углами и равными сторонами. Пример шахматной доски меня убеждает, что из правильных: четырехугольников тоже можно составить правильный паркет.

На примере пчелиных сот убеждаемся, что паркет можно составить и из правильных шестиугольников. Пчелы бессознательно решают математическую задачу – они стараются придать сотам такую форму, чтобы при заданном объёме на них шло как можно меньше воска. И хотя они не знают математики, но точно решают эту задачу. Пчелам помогает решать эту задачу инстинкт.

В свою очередь, правильные шестиугольники состоят из правильных треугольников, поэтому паркеты из правильных треугольников тоже существуют

Выясним, из каких ещё правильных многоугольников можно составить паркет?

Можно ли замостить плоскость правильными пятиугольниками?

Гео­метрические фигуры могут «встретиться» в вершине паркета только тогда, когда сумма их углов составляет 360 градусов, иначе они не сомкнуться вокруг вершины или «нале­зут» друг на друга).

Итак, главное условие, необходимое для построения паркетов:

Сумма углов многоугольников в узле паркета должна равняться 360 º

Пусть в каждой точке плоскости сходятся m одинаковых правильных n -угольников, то должно выполняться равенство:

После преобразований получим:

Если n =3, m =6 (6 треугольников в узле).

Если n =4, m =4 (4 четырёхугольника в узле).

Если n =5, m =3,333333… Но m не может быть дробным числом, число многоугольников должно быть натуральное.

Значит, пятиугольниками заполнить плоскость нельзя.

Если n =6, m =3 (шестиугольника)

Для п ≥ 7 не существует правильных многоугольников, для которых бы выполнялось главное условие. Значит, паркет из этих многоугольников ( п > 7; 8; 9… ) построить нельзя!

Вывод: Наше предположение оказалось верным.

Мы убедились в том, что паркет можно построить из:

На основе этих 3 правильных многоугольников можно составить различные правильные паркеты.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Замощения

Несложно замостить плоскость паркетом из правильных треугольников, квадратов или шестиугольников (под замощением мы понимаем такую укладку, при которой вершины каждой фигуры прикладываются только к вершинам соседних фигур и не возникает ситуации, когда вершина приложилась к стороне). Примеры таких замощений приведены на рис. 1.

Никакими другими правильными n-угольниками покрыть плоскость без пробелов и наложений не получится. Вот как можно это объяснить. Как известно, сумма внутренних углов любого n-угольника равна (n – 2) · 180°. Поскольку все углы правильного n-угольника одинаковые, то градусная мера каждого угла есть . Если плоскость можно замостить такими фигурами, то в каждой вершине сходится k многоугольников (для некоторого k). Сумма углов при этой вершине должна составлять 360°, поэтому . После нескольких простых преобразований это равенство превращается в такое: . Но, как легко проверить, последнее уравнение имеет только три пары решений, если считать, что n и k натуральные числа: k = 3, n = 6; k = 4, n = 4 или k = 6, n = 3. Этим парам чисел как раз и соответствуют приведенные на рис. 1 замощения.

А какими другими многоугольниками можно замостить плоскость без пробелов и наложений?

Видео:ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

Задача

а) Докажите, что любым треугольником можно замостить плоскость.

б) Докажите, что любым четырёхугольником (как выпуклым, так и невыпуклым) можно замостить плоскость.

в) Приведите пример пятиугольника, которым можно замостить плоскость.

г) Приведите пример шестиугольника, которым нельзя замостить плоскость.

д) Приведите пример n-угольника для какого-либо n > 6, которым можно замостить плоскость.

Видео:32 Четыре паркета, или Отражения треугольника относительно его сторонСкачать

Подсказка 1

В пунктах а), в), д) можно попытаться составить из одинаковых фигур «полоски», которыми потом легко замостить всю плоскость.

Пункт б): сложите из двух одинаковых четырехугольников шестиугольник, у которого противоположные стороны попарно параллельны. Такими шестиугольниками замостить плоскость уже достаточно просто.

Пункт г): используйте тот факт, что сумма углов при каждой вершине должна быть равна 360°.

Видео:Треугольники. 7 класс.Скачать

Подсказка 2

В пункте д) можно попробовать действовать и по-другому: немного менять уже имеющиеся фигуры, чтобы получались новые замощения.

🔍 Видео

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Вся геометрия треугольника в одной задаче. Планиметрия. ЕГЭ 2023 математика задача 16Скачать

Хитрый периметрСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Геометрия Раскрыта тайна площадей треугольниковСкачать

Первый признак равенства треугольников. 7 класс.Скачать

ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать