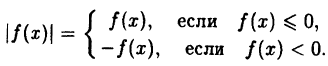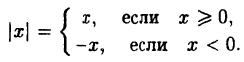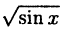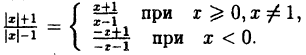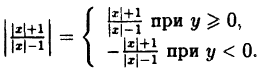Параллельный перенос и его свойства
- Содержание
- Общие сведения о параллельном переносе
- Свойства параллельного переноса
- Повторение темы о параллельном переносе
- Свойства, которыми обладает параллельный перенос в пространстве
- Истрия и применение в науке
- Примеры из жизни
- Преобразования декартовой системы координат с примерами решения
- Преобразования декартовой системы координат
- Параллельный перенос и поворот системы координат
- Полярные координаты. Замечательные кривые
- Преобразования графиков функций с примерами решения и образцами выполнения
- Параллельный перенос графиков
- Сжатие и растяжение графиков
- Построение графиков с модулями
- Построение графиков функций с примерами
- 🔥 Видео
Видео:Коллинеарность векторовСкачать

Содержание
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Общие сведения о параллельном переносе
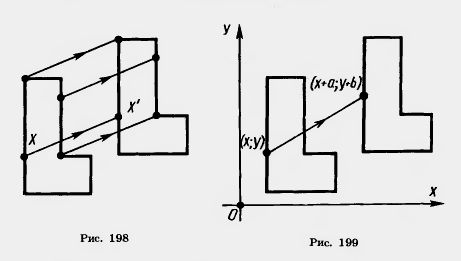
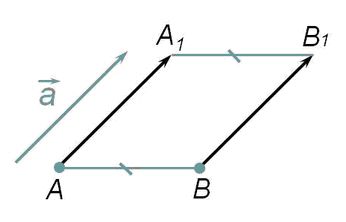
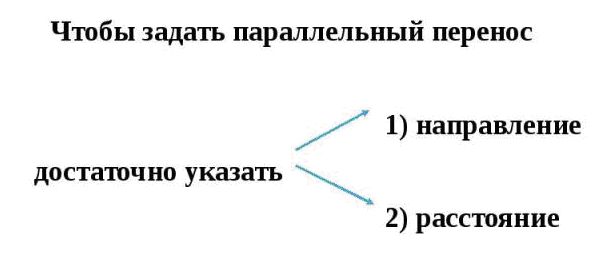
Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (рис. 198). Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении», которое само нуждается в точном определении. В связи с этим параллельному переносу мы дадим другое, отвечающее тому же наглядному представлению, но уже строгое определение.
Введем на плоскости декартовы координаты х, у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами x’ = x + а, у’ = у + b.
Эти формулы выражают координаты х’, у’ точки, в которую переходит точка (х; у) при параллельном переносе.
Видео:Геометрия и группы. Алексей Савватеев. Лекция 2.3. Параллельный переносСкачать

Свойства параллельного переноса
Параллельный перенос есть движение.
Действительно, две произвольные точки А(х1; у1) к В (х2; у2) переходят при параллельном переносе в точки А’ (х1 +а; у1 + b), В'(х2 + а; y2+b). Поэтому
АВ 2 =(х2-х1) 2 + (у2-у1 ) 2
Отсюда АВ=А’В’. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать.
Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
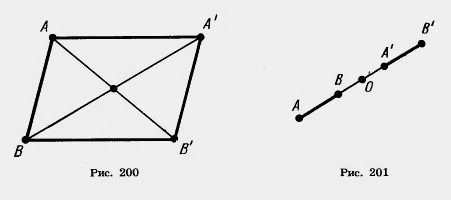
Действительно, пусть точки A (x1; y1) и В (x2; y2) переходят в точки A'(x1+а; y1 + b) и В’ (х2 + а; y2 + b) (рис. 200). Середина отрезка АВ’ имеет координаты
Те же координаты имеет и середина отрезка А’В. Отсюда следует, что диагонали четырехугольника АА’В’В пересекаются и точкой пересечения делятся пополам. Значит, этот четырехугольник — параллелограмм. А у параллелограмма противолежащие стороны А А’ и ВВ’ параллельны и равны.
Заметим, что у параллелограмма АА’В’В параллельны и две другие противолежащие стороны — АВ и А ‘В’. Отсюда следует, что при параллельном, переносе прямая переходит в параллельную прямую (или в себя).
Замечание. В предыдущем доказательстве предполагалось, что точка В не лежит на прямой АА’. В случае, когда точка В лежит на прямой АА’, точка В’ тоже лежит на этой прямой, так как середина отрезка АВ’ совпадает с серединой отрезка ВА’ (рис. 201). Значит, все точки А, В, А’, В’ лежат на одной прямой. Далее,
Таким образом, в этом случае точки АиВ смещаются по прямой АВ на одно и то же расстояние 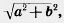
Видео:9 класс, 32 урок, Параллельный переносСкачать

Повторение темы о параллельном переносе
Мы с вами уже познакомились с такой темой, как параллельный перенос. На этом уроке вы узнали, что такое преобразование на плоскости, где все точки перемещаются на одно и то же расстояние, считается параллельным переносом.
Из данного урока, каждому из вас стало понятно, что параллельный перенос является движением, так как при таком переносе любая прямая переходит в такую же параллельную ей прямую.
Если мы посмотрим на рисунок, то можем наглядно представить такое движение, как сдвиг площади в направлении данного вектора на его длину.
Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Свойства, которыми обладает параллельный перенос в пространстве
• Во-первых, параллельный перенос является движением;
• Во-вторых, при выполнении этого действия все точки смещаются по параллельным прямым и притом на одно и то же расстояние;
• В-третьих, при таком переносе прямая имеет свойство переходить в такую же параллельную прямую или в себя саму;
• В-четвертых, независимо от того, какими точками были A и A’, но точка A переходит в точку A’.
• В-пятых, при таком переносе, т.е параллельном переносе в пространстве, в любом случае плоскость имеет свойство переходить в себя саму или же такую же параллельную ей плоскость.
Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Истрия и применение в науке
Как правило, в каждого понятия есть свой первооткрыватель, но автор параллельного переноса в пространстве, на жаль, нам неизвестен. А вот применение параллельного переноса в пространстве довольно широко. Как правило, такой перенос используют при преобразовании графической функции в математике, в механике, а также в кристаллографии.
Но если рассматривать трансляция или кристаллографию, то в этом случае перенос приобретает симметричное преобразование, в котором узел пространственной решётки должен совпасть с идентичным ближайшим узлом. В принципе, трансляцию можно отнести к частному случаю параллельного переноса, так как при сдвиге на определенный вектор ее свойства в данной системе не изменяются, а являются вектором трансляции и для нее свойственна трансляционная симметрия.
Видео:ГРАФИК ФУНКЦИЙ — Сдвиги Графика Функции, Как строить Графики Функции // Алгебра 8 классСкачать

Примеры из жизни
В повседневной жизни мы с вами также постоянно сталкиваемся с примерами параллельного переноса в пространстве. Таким наглядным примером может быть, применяемая в строительной индустрии скользящая опалубка, этот процесс мы можем наблюдать и при перестановке мебели в квартире, да и следы от подошвы нам также напоминают о параллельном переносе в пространстве.
А также, параллельный перенос можно встретить и в таких необычных ситуациях:
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Преобразования декартовой системы координат с примерами решения
Содержание:
Видео:Преобразование графиков функций. y= f(x + n). Сдвиг по оси OX. 10 класс.Скачать

Преобразования декартовой системы координат
Параллельный перенос и поворот системы координат
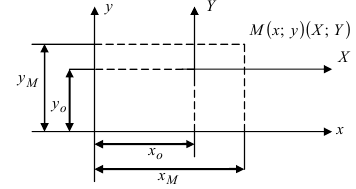
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):
Рис. 46. Параллельный перенос одной системы координат относительно другой системы.
Систему координат
Пример:
Дана точка М(3;2) и начало новой системы координат 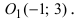
Решение:
Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим 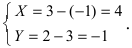
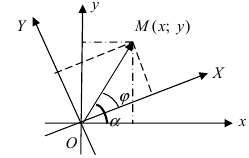
2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 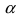
Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны 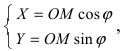
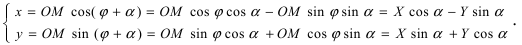
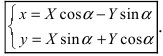
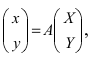
Найдем обратное преобразование системы координат, найдем матрицу 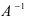
Найдем алгебраические дополнения всех элементов
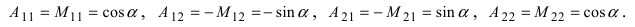
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.
Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.
Таким образом, имеем 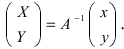
Пример:
Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол
Решение:
Воспользуемся полученными формулами 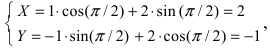
Рассмотрим применение преобразования координат:
а) Преобразовать уравнение параболы 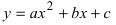
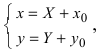
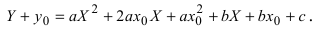
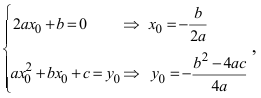
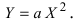
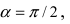
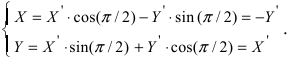
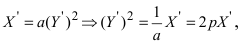
Пример:
Преобразовать уравнение параболы 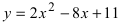
Решение:
Найдем начало отсчета новой системы координат после параллельного переноса 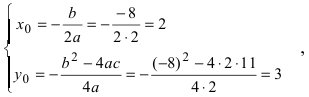
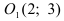
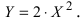
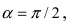
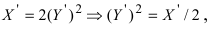
б) Выяснить, какую кривую описывает функция
Проведем следующее преобразование 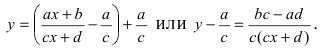
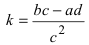
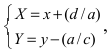
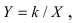
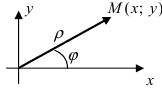
Полярные координаты. Замечательные кривые
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 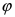
Рис. 48. Полярная система координат.
Главными значениями угла 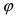
Рассмотрим замечательные кривые в полярной системе координат:
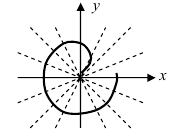
1. Спираль Архимеда 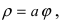
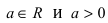
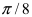
Рис. 49. Спираль (улитка) Архимеда.
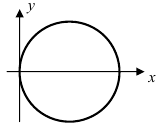
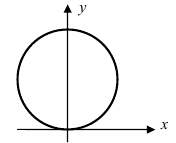
2. Уравнение окружности: уравнение 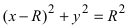
Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.
3. Уравнение 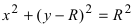
Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.
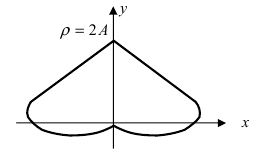
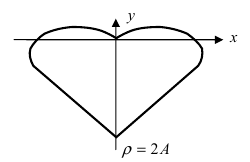
4. Кардиоиды:
Рис. 52. Кардиоида
Рис. 53. Кардиоида
Аналогично выглядят кардиоиды 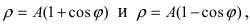
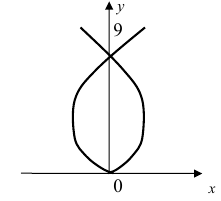
5. Петля: 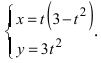
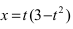
Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Вектор. Определение. Коллинеарные векторы. Равные векторы.Скачать

Преобразования графиков функций с примерами решения и образцами выполнения
Параллельный перенос, сжатие и растяжение графиков. Построение графиков с модулями.
Графики многих функций можно получить из ранее рассмотренных с помощью элементарных геометрических преобразований: параллельного переноса, сжатия, растяжения, симметричного отображения. Рассмотрим некоторые из этих преобразований. Для каждого из элементарных преобразований предлагается два способа построения графика: с помощью преобразования графика и с помощью преобразования системы координат. Обучающийся должен выбрать тот, который кажется ему проще и овладеть им. В каждом случае считается известным график функции у = f(х).
Видео:11 класс, 12 урок, Параллельный переносСкачать

Параллельный перенос графиков
График функции у = /(x) + Ь получается из графика функции у = f(х) с помощью его переноса на вектор b = (0; b). Действительно, в этом случае ко всем ординатам графика у = f(х) прибавляется величина b, что означает сдвиг графика вдоль оси Оу. Если b > 0, то график функции у = f(х) переносится вверх параллельно оси Oy на b, если b 0 — вниз, если b 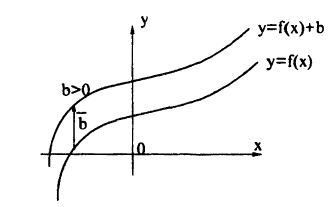
Пример:
График функции у = x² — 1 (рис. 50) смещен на 1 вниз параллельно оси Oy относительно графика функции у = х².
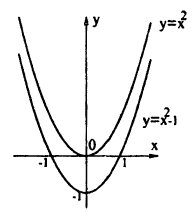
График функции у = f(x+a) получается с помощью переноса графика функции у = f(x) на вектор а = (—а;0). Действительно, перейдя к новым координатам X = х + α, Y = у параллельным переносом вдоль оси Ox на —а, заметим, что относительно новых координат получится исходный график функции Y = f(X). Если а > 0, то старые координаты получаются из новых сдвигом направо вдоль оси Ox на α, т.к. х = X — а. Если же сдвигать график, а не систему координат, то его нужно двигать в противоположном направлении — налево. Итак, если а > 0, то график функции у = f(x) переносится налево параллельно оси Ox на а, если а 0 — вправо, если α 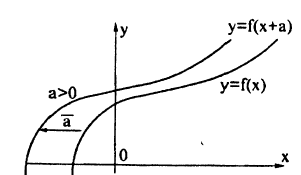
Видео:Преобразование системы координат (параллельный сдвиг)Скачать

Сжатие и растяжение графиков
График функции у = kf(x), где к ∈ R, получается с помощью ’’растяжения” графика функции у = f(x) в к раз в направлении от оси Ох. ’’Растяжение” здесь понимается как умножение на к ординат всех точек графика у = f(x)∙ При k > 1 это будет действительно растяжение в к раз от оси Ox вдоль оси Оу. При 0 0 можно исправить значения по оси Оу, умножив их на k. При k 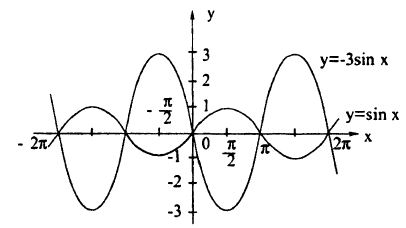
При k > 1 график функции у = f(x) сжимается в k раз к оси Oy вдоль оси Ох; при 0 0 можно исправить значения по оси Ох, поделив их на k. При k 
Пользуясь изложенными методами, приведем последовательность преобразований при построении графика функции у = f(kx + b), если дан график функции у = f(x):
- нарисовать график функции у = f(x);
- получить график функции у = f(x + b), сдвинув исходный на вектор b = (-b; 0), как описано в п. 5.1;
- получить график функции у = f(kx + b), “сжав” предыдущий в к раз к оси Оу, как описано выше.
Пример:
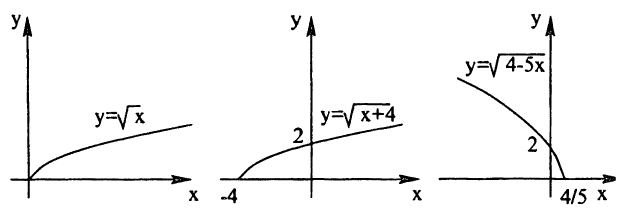
Написать последовательность преобразований и построить график функции у = 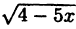
Решение:
- нарисуем график функции у = √х;
- о получим график функции у =
, сдвинув исходный на 4 единицы влево вдоль оси Ох;
- о получим график функции у =
, сжав предыдущий в 5 раз к оси Oy и затем отобразив симметрично относительно оси Оу.
Построение графика показано на рис. 55
Замечание:
Теперь понятно, что если функция у = f(x) периодическая с периодом Т, то функция у = К ∙ f(kx + b) + а тоже периодическая с периодом T₁ = 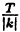
Видео:Физика | Ликбез по векторамСкачать

Построение графиков с модулями
График функции у = ∣f(x)∣ получается из графика функции у = f(x) следующим образом (рис. 56)
- все части графика функции у = f(x), лежащие ниже оси Ох, следует отобразить вверх симметрично относительно этой оси;
- оставшиеся внизу части исходного графика следует стереть.
Действительно, по определению модуля действительного числа имеем:
(5.1)
Таким образом, те участки исходного графика, которые лежат не ниже оси Ox (f(x) ≥ 0), менять не нужно, а для тех участков, которые лежат ниже оси Ох, нужно построить функцию у = —f(x). В соответствии с п. 5.2 это получается симметричным отображением исходного графика относительно оси Ох. Заметим, что полученный график лежит не ниже оси Ох, что естественно, т.к. |f(x)| ≥ 0 для ∀x ∈ D(f).
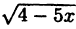
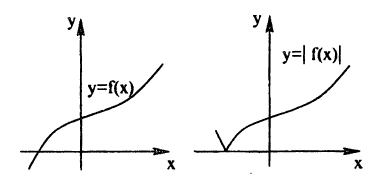
Пример:
Построение графика функции у = |х² — 1| показано на рис. 57.
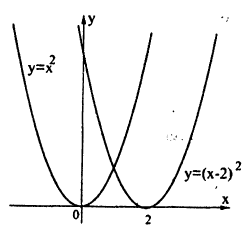
График функции у = f (|x|) получается из графика функции у = f(х) следующим образом (рис. 58):
- все части графика функции у = f(x), лежащие слева от оси Оу, следует стереть;
- о оставшуюся часть графика следует отобразить налево симметрично относительно оси Оу.
Действительно, по определению модуля действительного числа имеем:
(5.2)
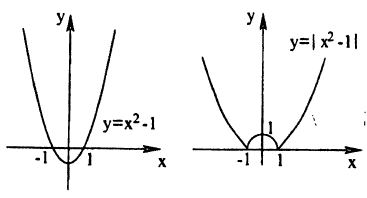
Таким образом, не нужно изменять те участки исходного графика, для которых х ≥ 0, а для х 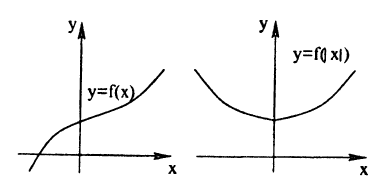
Пример:
Построение графика функции у = (|x| — 2)² показано на рис. 59
Элементарными методами можно строить эскизы графиков более сложных функций.
Пример:
Построить эскиз графика у =
Решение:
Построение графика показано на рис. 60. Заметим, что график отсутствует там, где sin х 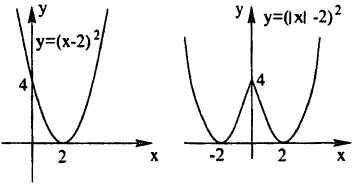
Кроме того, так как √u > и при 0 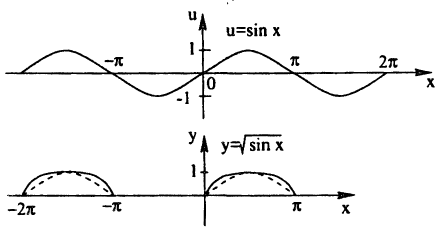
Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Построение графиков функций с примерами
Пример:
C помощью элементарных преобразований постройте график функции: у = x² — х — 2.
Решение:
Выделим полный квадрат из правой части уравнения функции: у = x² — х — 2 ⇔ y = x²-x+ 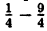
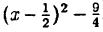
1) y =x²
2) у =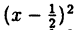
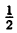
3) у = 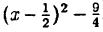
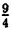
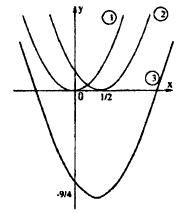
Пример:
Используя сложение, деление функций, постройте график функции: у = х + 
Решение:
В одних осях координат нарисуем графики следующих функций (рис. 62):
1) у = х,
2) y=
3) y = x + 
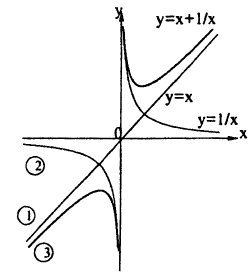
Пример:
Постройте график сложной функции у = sin² х.
Решение:
В одних осях координат нарисуем графики функций:
1) y = sin x,
2) y = sin² х.
Учитывая, что квадрат числа меньшего единицы, меньше исходного числа, получим график (рис. 63)
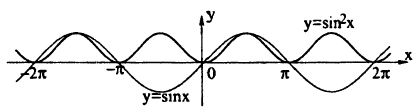
Пример:
Постройте график функции в полярной системе координат: r = 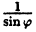
Решение:
Вычислим значения г для некоторых значений 
 | 0 | 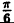 | 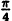 | 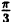 | 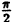 |
| r | ∞ | 2 | 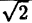 | 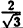 | ∞ |
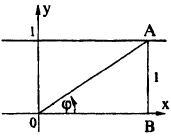
Соединив плавной линией найденные точки, получим линию вдоль оси Ох, проходящую через точку (0;1). Докажем что эта линия — прямая (рис. 64). Действительно: из Δ ОAВ ⇒ cos 
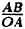
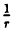
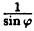
Пример:
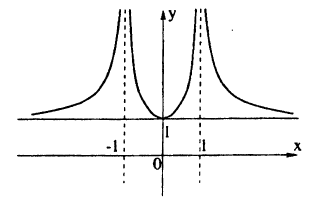
Постройте линию, описываемую уравнением, у =
Решение:
Сначала построим график функции у = 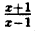
Наконец, строим линию описываемую уравнением у = 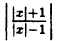
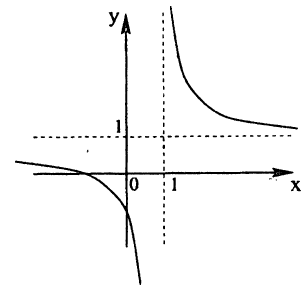
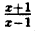
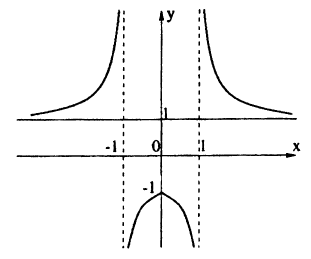
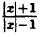
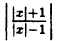
Пример:
Постройте линию, описываемую уравнением у =
Решение:
Для построения графика данного примера сначала постройте график функции у =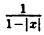
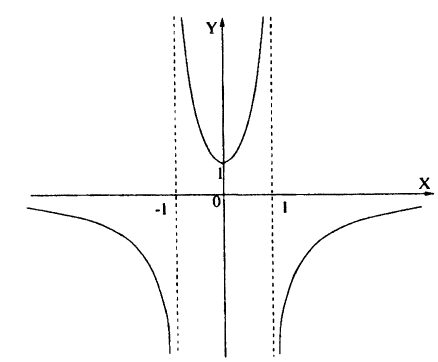
Пример:
Постройте линию, описываемую уравнением у = |х² — х -2|.
Решение:
Для построения графика данного примера сначала постройте график функции у = х² — х — 2. Затем отразите симметрично оси Ox ту часть графика, которая осталась снизу от оси Ох. Затем сотрите ту часть графика, которая расположена в нижней полуплоскости.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🔥 Видео
Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Геометрия 9 класс : Параллельный перенос и поворотСкачать

Тема: Движения. Урок: Что такое векторыСкачать

Разложение вектора на неколлинеарные вектора.Скачать

АвтоГраф. Векторы и параллельный переносСкачать

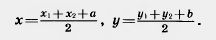
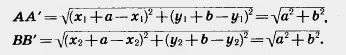


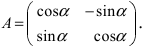
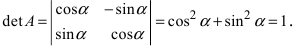
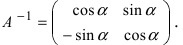
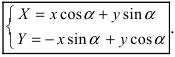
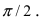
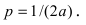
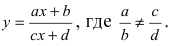
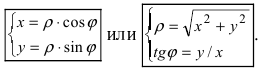
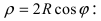
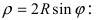
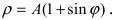
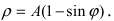
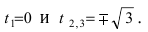

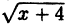 , сдвинув исходный на 4 единицы влево вдоль оси Ох;
, сдвинув исходный на 4 единицы влево вдоль оси Ох;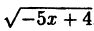 , сжав предыдущий в 5 раз к оси Oy и затем отобразив симметрично относительно оси Оу.
, сжав предыдущий в 5 раз к оси Oy и затем отобразив симметрично относительно оси Оу.