Перейдем сразу к решению задач на построение методом параллельного переноса.
Задача 6.34. Даны две окружности Fv F2 и прямая I. Провести прямую, параллельную прямой I, на которой окружности Fr и F2 высекают равные хорды.
Пусть прямая V искомая, т.е. прямая V высекает на данных окружностях равные хорды АВ иА’В’ (рис. 6.34).
Тогда точки АиА’,ВиВ’ можно рассматривать как соответственные при параллельном переносе ОхО<.
Так как точка А’ является образом точки А, принадлежащей окружности Fb то точка Л’ принадлежит образу окружности F,. Следовательно, А’ — общая точка окружности F2 и образа окружности Fj при параллельном переносе 0-[0[. Построив точку А’, находим на окружности F] ее прообраз. _
Если F2 есть образ точки Fx при параллельном переносе OjOf, то задача имеет бесконечное множество решений. В остальных случаях задача имеет не более четырех решений, так как окружность F2 имеет не более двух точек пересечения с окружностью F <и не более двух точек пересечения с окружностью F» (образ окружности Fj при параллельном переносе ОуО<).
Задача 6.35. Между двумя данными окружностями (О, Р) и (Q, г) провести отрезок данной длины (а) параллельно данной прямой (АР).
Анализ. Допустим, что задача решена и отрезок CD является искомым (рис. 6.35). Если мысленно будем перемещать отрезок CD параллельно самому себе, оставляя один из его концов D скользящим по данной окружности (Q, г), то ясно, что другой конец (С) отрезка CD опишет в это время окружность того же радиуса (г), имеющую центр в некоторой точке Р, отстоящей от точки Q на расстояние, равное отрезку а. Отсюда следует, что, построив окружность (Р, г), мы сможем построить и искомые отрезки.
Построение. 1. Проведем из точки Q отрезок QP, который параллелен прямой АВ и равен отрезку а.
- 2. Около точки Р радиусом, равным г, опишем вспомогательную окружность (Р, г).
- 3. Обозначим буквами С и ? те точки, в которых вспомогательная окружность (Р, г) пересечет окружность (О, Р).
- 4. Если из точек С и ? проведем прямые, параллельные прямой АВ, то они пересекут окружность (Q, г) в некоторых точках D и F.
Отрезки CD и ?? — искомые.
Доказательство несложное, а поэтому предлагаем провести самостоятельно.
Исследование. Если вспомогательная окружность (Р, г) пересекает данную окружность (О, К), то задача имеет два решения.
Если окружность (Р, г) будет лишь касаться окружности (О, Р), то задача имеет одно решение.
Наконец, если окружность (Р, г) не будет ни касаться окружности, ни пересекать ее, то задача не имеет решений.
Задача 6.36. Даны окружность и прямая I. На окружности даны две точки А и В. Найти на окружности такую точку М, чтобы прямые МА и МВ пересекали I в точках К и N таким образом, что KN — а, где а — заданный отрезок.
Построим точку А’ (рис. 6.36) так, чтобы NKAA’ был параллелограммом (А’ получается из А при помощи известного параллельного переноса). Поскольку ZBNA’ = ZBMA, а последний известен, то точка N находится как пересечение I с соответствующим геометрическим местом точек. Следует также рассмотреть случай расположения точки М на другой дуге АВ.
- Параллельный перенос, поворот плоскости и подобные треугольники
- Корзина
- Параллельный перенос
- Поворот плоскости вокруг точки на угол
- Подобные треугольники
- При каком условии можно отобразить параллельным переносом окружность на окружность?
- Каким условиям должны удовлетворять два квадрата, чтобы один из них можно было получить из другого при помощи параллельного переноса?
- Какими условиями должны удовлетворять 2 квадрата, чтобы 1 из них можно было получить из другого при параллельном переносе?
- Помогите пожалуйста♥?
- Точки (−1 ; 5) и (7 ; −1) задают концы диаметра окружности?
- При каком условии в четырехугольник можно вписать окружность?
- Можно ли вокруг параллелограмма описать окружность?
- Диаметр окружности равен 88 км?
- Каким условиям должны удовлетворять два равносторонних треугольника чтобы один из них можно было получить из другого при помощи параллельного переноса?
- Хорда окружности равна 10 см?
- Диаметр окружности равен 4а?
- 💥 Видео
Видео:63 Окружность и параллельный переносСкачать

Параллельный перенос, поворот плоскости и подобные треугольники
Корзина

Теоретический урок по предмету математики для решения задач по теме «Параллельный перенос, поворот плоскости и подобные треугольники».
Содержание данной онлайн страницы электронного справочника для школьников:
- – тема «Параллельный перенос» представлена на примере решения задач 145 — 148;
- – в контрольных работах с номерами 149 — 154 данной рабочей тетради по математике рассматривается поворот плоскости вокруг точки на угол;
- – повторение курса геометрии 9 класса в решениях приведено на примере заданий 155 — 173: углы треугольника, площадь треугольника через катеты и гипотенузу, вычисление радиуса описанной окружности, стороны ромба, подобные треугольники.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Параллельный перенос


Параллельным переносом на вектор 


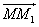

Задача 145.



A → A1 : 


B → B1 : 


Теорема:
При параллельном переносе на вектор 

f – параллельный перенос на вектор 
M 

N 



Точка M переводится движением в точку M1 с условием, что два вектора равны: M 



Точка N переводится движением в точку N1 с условием, что два вектора равны: N 



Следовательно, полученные отрезки параллельны MM1 || NN1 и построенные отрезки равны MM1 = NN1
Значит, четырехугольник MM1N1N – параллелограмм.
Поэтому MN = M1N1, значит f – движение.

Задача 146.
A 




B 




C 


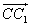


A 




B 




C 


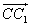



Задача 147.
точка D лежит на AC: D 
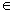
точка C лежит на AD: C 
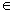
BC 
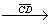
б) Доказать: ABB1D – равнобедренная трапеция
1) От точки B проведем прямую a, параллельную вектору 
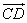

2) Точка B переводится движением в точку B1



3) Проведем прямую B1D, параллельную отрезку BC:
Рассмотрим четырехугольник BB1DC.
Т.к. основания BB1 || CD и боковые стороны BC || BD параллельны, то BB1DC – параллелограмм (по определению)
По свойству параллелограмма:
основания BB1 = CD и боковые стороны BC = BD равны, но AB = BC, тогда AB = B1D
Т.к. BB1 || AD параллельны и AB 
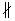
Т.к. AB = B1D, то ABB1D – равнобедренная трапеция.
Задача 148.
Дано: 
вектор 
окр (O;R) 

ΔABC 

EFPQ 

как показано на рисунке.
Видео:Вписанные углы в окружностиСкачать

Поворот плоскости вокруг точки на угол
Определение:




O – центр поворота
α – угол поворота
Задача 149.


α = 75° (против часовой стрелки)
O – центр поворота
1) A 
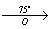


2) B 
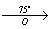


Теорема:
Поворот является движением.


α – угол поворота (против часовой стрелки)
точка O – центр поворота
Тогда треугольники равны ΔOMN = ΔOM1N1 по двум сторонам и углу между ними:




Тогда MN = M1N1, значит, f – движение.
Задача 150.
точка O – центр поворота


1) A 
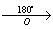


2) B 
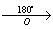


Задача 151.
точка A – центр поворота
α = 160° (против часовой стрелки)
1) B 
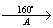


2) C 
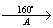


Задача 152.
точка O – центр поворота


1) A 
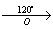


2) B 
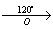


Задача 153.
точка C – центр окружности (C; R)
точка O – центр поворота
угол поворота α = 60° (против часовой стрелки)
а) точка C и точка O не совпадают
б) точка C и точка O совпадают


1) проведем луч CO
2) C 
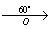



Т.к. точка О – центр поворота и точка С – центр окружности совпадают, то окружности (C;R) и (C1;R) будут тоже совпадать.

Задача 154.
Δ ABC – равнобедренный, равносторонний
D – точка пересечения биссектрис
D – центр поворота
угол поворота α = 120°
ΔABC 

Т.к. Δ ABC – правильный, то все углы в нем равны 60°.
Т.к. точка D – центр описанной и вписанной окружности, то
Δ ABD = Δ BDC = Δ DAC (по трем сторонам).
Следовательно, что 





A 

B 

C 

Таким образом, Δ ABC отображается на себя.
Повторение.
Задача 155.






Найти: наибольший угол треугольника
Пусть x – коэффициент пропорциональности. Зная, что сумма углов в треугольнике равна 180°, составим и решим уравнение:
3x + 7x + 8x = 180
Наибольший угол 

Задача 156.
треугольник ΔABC – равнобедренный,
один угол больше другого:






Найти: угол при основании треугольника
Пусть x° – угол при основании треугольника. Зная, что сумма углов в треугольнике составляет 180°, составим и решим уравнение:
(x + 60°) + x + x = 180°
Значит, 

Задача 157.
треугольник ΔABC – прямоугольный
c = 26 см – гипотенуза
Найти: больший катет b
Пусть x – коэффициент пропорциональности. По теореме Пифагора составим и решим уравнение:
(5x) 2 + (12x) 2 = 26 2
25x 2 + 144x 2 = 676
b = 12 • 2 = 24 (см)
Задача 158.


c = 13 – гипотенуза
По теореме Пифагора получаем:
a = 
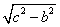

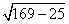

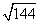
Тогда площадь треугольника
SΔABC = 


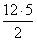
= 30 (квадратных единиц)
Задача 159.
треугольник ΔABC – равнобедренный,


c = 4 
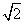
Найти: площадь треугольника SΔABC = ?
SΔABC = 

Т.к. Δ ABC – равнобедренный, то углы при основании по 45° и катеты равны a = b.
По теореме Пифагора получаем:
Тогда (4 
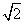
Тогда площадь треугольника
SΔABC = 


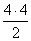
= 8 (квадратных единиц)
Задача 160.




Найти: радиус описанной окружности R = ?
Т.к. AH – медиана, то CH = 

По теореме Пифагора получаем:
Тогда CH = 


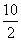
Точка H – центр описанной окружности
Т.к. R = AH, то R = AH = CH = 5 ед.
Задача 161.


соотношение острых углов




AC = 4 
Найти: радиус описанной окружности R = ?


Тогда 



Следовательно, BC = 

По теореме Пифагора получаем:
AC 2 + 
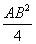
AC 2 = 

AB 2 = 
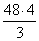
R = AD = BD = 8 : 2 = 4 (ед)
Задача 162.




радиус описанной окружности
Тогда AB = 2,5 • 2 = 5
По теореме Пифагора получаем:
AC = 
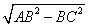

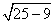

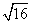




tg 


0,6 = 
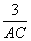

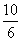
Задача 164.


Найти: 



Т.к. AH = AC, то Δ AHC – равнобедренный.
Точка H – радиус вписанной окружности, поэтому AH = CH, но AH = AC, следовательно, AH = CH = AC.
Тогда Δ AHC – равносторонний.
Значит, 





Задача 165.
треугольник Δ ABC – правильный, равносторонний,
SΔABC = 
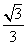
Найти: длину биссектрисы BH = ?


Рассмотрим Δ ABC – равнобедренный, где




Тогда BH – медиана, высота.
Значит, перпендикулярны отрезки BH 
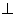
Рассмотрим треугольники Δ ABH и Δ BHC.
AB = BC, по условию.
AH = CH, BH – медиана.
Значит, треугольники равны Δ ABH = Δ BHC.
Т.е. SΔABH = 




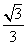

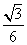
SΔABH = 

Рассмотрим треугольник Δ ABH.
Т.к. BH – биссектриса, то угол 

AH = 

SΔABH = 


AB • BH = 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
AB 2 = 

BH 2 = 

BH = 
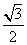
Используя результат (**) в уравнении (*), получаем
AB • 
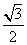

AB 2 = 
AB = 
Тогда AB • BH = 






Задача 166.
треугольник Δ ABC – правильный, равносторонний,


R = 
Найти: площадь треугольника
Рассмотрим Δ ABO (AO = BO = R) 

Проведем из вершины O к AB высоту OH.
Рассмотрим Δ AOH, где 

Т.к. 







OH = 


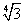

По теореме Пифагора получаем:
OH 2 + AH 2 = OA 2

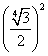

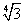



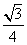
= 
AH 2 = 
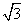

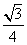

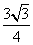



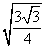

Тогда площадь треугольника
SΔAOH = 




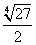

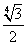

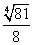

Следовательно, SΔABO = 2 • SΔAOH = 2 • 
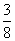


Тогда площадь треугольника
SΔABC = 3 • SΔABO = 3 • 


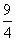




Площадь ромба SABCD = 384
Соотношение диагоналей ромба:
Найти: сторону ромба AB = ?
SABCD = 

Пусть x – коэффициент пропорциональности. Тогда
SABCD = 

Следовательно, диагональ BD = 4x = 4 • 8 = 32
AC = 3x = 3 • 8 = 24
Поэтому половина диагонали AO = 



BO = 



По теореме Пифагора получаем:
AO 2 + BO 2 = AB 2
Сторона ромба AB = 
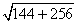

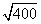
Задача 168.
треугольник Δ ABD – равнобедренный,


Найти: площадь треугольника
SΔABD = 

Проведем высоту BH к основанию AD.
По свойству равнобедренного треугольника:
BH – медиана, биссектриса, высота.
Т.к. BH – медиана, то AH = DH = 16 : 2 = 8 (ед.)
Рассмотрим треугольник Δ ABH, где угол 

По теореме Пифагора получаем:
AB 2 = AH 2 + BH 2
BH = 
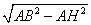

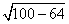

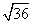
Тогда площадь треугольника
SΔABD = 



Ответ: площадь треугольника SΔABD = 48 кв.ед.

Задача 169.
треугольник Δ ABC –равнобедренный,
основание AC больше высоты BH на 15: AC > BH на 15
Найти: основание AC = ?
Т.к. треугольник Δ ABC –равнобедренный, то BH – высота, медиана, биссектриса.
Тогда AC = AH + CH = AH + AH = 2 AH
Рассмотрим Δ ABH – прямоугольный.
Пусть AC = (x) ед. 


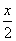
Тогда AB = (x – 15) ед. (по условию).
По теореме Пифагора решим уравнение:
(x – 15) 2 = ( 
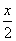



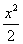
4 (x 2 – 30x) = x 2
4x 2 – 120x = x 2
3x 2 – 120x = 0 | : x
Таким образом, 40 ед. – длина основания.
Ответ: AC = 40 ед.
Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Подобные треугольники
Задача 170.






CH – биссектриса угла 

Доказать: подобие треугольников
Δ BHC 









Т.к. CH – биссектриса угла 





Рассмотрим Δ BHC








Тогда 



Поэтому треугольники подобны Δ BHC 



верхнее основание BC = 4 см
нижнее основание AD = 10 см
диагональ BD = 8 см
часть диагонали BO = ?
соотношение периметров треугольников


Углы равны 



Углы равны 



Тогда треугольники подобны Δ BCO 




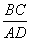

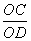







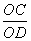













Пусть BO = x, AO = 8 – x. Тогда 10x = 4 • (8 – x)
x = 2 

Следовательно, BO = 2 



Ответ: BO = 2 



Задача 172.
ΔABC 



P (ΔABC) = 12 +16 + 20 = 48 (дм)
Т.к. треугольники подобны, то

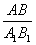

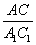




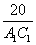


Тогда соотношение периметров треугольников

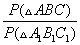
Из равенств (*) и (**) следует



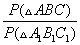




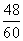

B1C1 = 
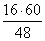
Тогда 





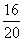



A1B1 = 
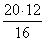
Задача 173.


стороны трапеции пересекаются в точке M:
Рассмотрим треугольники ΔAMD и ΔBMC:








Тогда, по первому признаку подобия треугольников:
треугольники подобны Δ AMD 


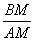

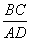

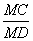


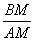

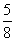
но AM = AB + BM = 3,9 + BM
8 • BM = 5 (3,9 + BM)

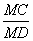

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

При каком условии можно отобразить параллельным переносом окружность на окружность?
Геометрия | 5 — 9 классы
При каком условии можно отобразить параллельным переносом окружность на окружность?
А) R1 не равен R2 б) R1 = R2 в) нельзя отобразить.
Не совсем понятно задание.
Окружность параллельным переносом всегда можно отобразить на другую окружность.
У полученной окружности сохранятся все свойства исходной окружности.
Радиус первой будет равен радиусу второй.
Вектор переноса может быть каким угодно.
А может в Вашей задаче вектор переноса оговаривается?
Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Каким условиям должны удовлетворять два квадрата, чтобы один из них можно было получить из другого при помощи параллельного переноса?
Каким условиям должны удовлетворять два квадрата, чтобы один из них можно было получить из другого при помощи параллельного переноса?
Видео:9 класс, 32 урок, Параллельный переносСкачать

Какими условиями должны удовлетворять 2 квадрата, чтобы 1 из них можно было получить из другого при параллельном переносе?
Какими условиями должны удовлетворять 2 квадрата, чтобы 1 из них можно было получить из другого при параллельном переносе?
Видео:Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Помогите пожалуйста♥?
При параллельном переносе окружности получена окружность, касающаяся данной окружности.
На какое расстояние перенесена параллельно эта окружность?
Видео:Поворот и параллельный перенос координатных осей. ЭллипсСкачать
Точки (−1 ; 5) и (7 ; −1) задают концы диаметра окружности?
Точки (−1 ; 5) и (7 ; −1) задают концы диаметра окружности.
Найдите параллельный перенос, при котором центр данной окружности переходит в точку ′ (−5 ; −3).
Запишите уравнения полученной окружности.
Видео:Геометрия и группы. Алексей Савватеев. Лекция 2.3. Параллельный переносСкачать

При каком условии в четырехугольник можно вписать окружность?
При каком условии в четырехугольник можно вписать окружность.
Видео:115 Параллельный переносСкачать

Можно ли вокруг параллелограмма описать окружность?
Можно ли вокруг параллелограмма описать окружность?
Если да, то при каком условии?
Видео:Нахождение истинной формы плоской фигуры методом плоско параллельного перемещенияСкачать

Диаметр окружности равен 88 км?
Диаметр окружности равен 88 км.
Чему равен радиус окружности?
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Каким условиям должны удовлетворять два равносторонних треугольника чтобы один из них можно было получить из другого при помощи параллельного переноса?
Каким условиям должны удовлетворять два равносторонних треугольника чтобы один из них можно было получить из другого при помощи параллельного переноса?
Видео:Найти центр и радиус окружностиСкачать

Хорда окружности равна 10 см?
Хорда окружности равна 10 см.
Через один конец хорды проведена касательная к окружности, а через другой — секущая, параллельная касательной.
Определить радиус окружности, если внутренний отрезок секущей равен 12 см.
Видео:9 класс. Параллельный переносСкачать

Диаметр окружности равен 4а?
Диаметр окружности равен 4а.
Укажите радиус окружности.
На этой странице сайта, в категории Геометрия размещен ответ на вопрос При каком условии можно отобразить параллельным переносом окружность на окружность?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.
AD = 26 2 + 2 + 2 = 6 16 + 6 = 26 Вот ответ.
💥 Видео
Урок 7. Окружность, круг и их элементы. ОГЭ. Вебинар |МатематикаСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Параллельный переносСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать