Как нарисовать траекторию движения точки по окружности (5 видео)

Траектория движения

Содержание

Определение и основные понятия траектории движения
Уравнение траектории движения
Обратимость движения
Параметры траектории движения
Примеры задач с решением
Движение тела по криволинейной траектории. Движение по окружности. Характеристики вращательного движения. Центростремительное ускорение
Как нарисовать траекторию движения точки по окружности
📸 Видео

Видео:Физика - движение по окружностиСкачать

Определение и основные понятия траектории движения

Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.

Линию, которую описывает частица при своем движении, называется траекторией движения.

В зависимости от формы траектории механическое движение можно разделить на:

прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
и криволинейное перемещение (траектория — кривая линия).

Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.

При движении точки с постоянным ускорением, которое описывает уравнение:

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Уравнение траектории движения

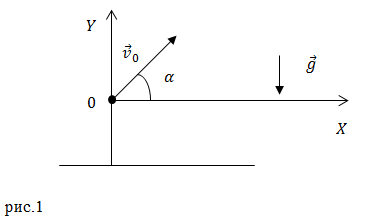
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.

Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:

Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:

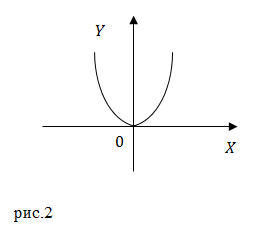
Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.

Вершина этой параболы находится в точке с координатами:

Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac$) от нее по $x$.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Обратимость движения

Из представления о траектории можно конкретизировать смысл обратимости механического движения.

Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.

Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Параметры траектории движения

Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:

Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки — это значит указать эти функции: [x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: [overline=overlineleft(tright)left(7right).]
Третьим способом описания движения является описание с помощью параметров траектории.

Путь — это скалярная величина, равная длине траектории.

Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:

Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:

где $s$ — путь точки по траектории; $t$ — время движения; $A$ — коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.

Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.

Видео:Объект по кругу в After Effects Как по кругу пустить объект и анимация по пути | TutorialСкачать

Примеры задач с решением

Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline=Aoverline+Bxoverline , $где $overline$, $overline$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit

Решение: Рассмотрим уравнение изменения скорости частицы:

Из этого уравнения следует, что:

Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):

Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:

Задание: Движение материальной точки в плоскости описывает система уравнений: $left< begin x=At. \ y=At(1+Bt) end right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.

Решение: Рассмотрим систему уравнений, которая задана в условии задачи:

Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:

Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:

Видео:Базовый Курс Adobe After Effects. Движение объекта по траектории пути движения. Урок №25.Скачать

Движение тела по криволинейной траектории. Движение по окружности. Характеристики вращательного движения. Центростремительное ускорение

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Вам хорошо известно, что в зависимости от формы траектории движение делится на прямолинейное и криволинейное. С прямолинейным движением мы научились работать на предыдущих уроках, а именно решать главную задачу механики для такого вида движения.

Однако ясно, что в реальном мире мы чаще всего имеем дело с криволинейным движением, когда траектория представляет собой кривую линию. Примерами такого движения является траектория тела, брошенного под углом к горизонту, движение Земли вокруг Солнца и даже траектория движения ваших глаз, следящих сейчас за этим конспектом.

Вопросу о том, как решается главная задача механики в случае криволинейного движения, и будет посвящен этот урок.

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Как нарисовать траекторию движения точки по окружности

КРИВЫЕ, КАК ТРАЕКТОРИИ ДВИЖЕНИЯ ТОЧЕК

Одним из древнейших способов образования кривых является кинематический способ, при котором кривая получается как траектория движения точки.

Кривая, которая получается как траектория движения точки, закрепленной на окружности, катящейся без скольжения по прямой, по окружности или другой кривой, называется циклоидальной, что в переводе с греческого языка означает «кругообразная, напоминающая о круге».

Рассмотрим сначала случай, когда окружность катится по прямой. Кривая, которую описывает точка, закрепленная на окружности, катящейся без скольжения по прямой, называется циклоидой.

Пусть окружность радиуса R катится по прямой а. С – точка, закрепленная на окружности, в начальный момент времени находящаяся в положении А (рис. 1). Отложим на прямой а отрезок АВ, равный длине окружности, т.е. АВ = 2 π R . Разделим этот отрезок на 8 равных частей точками А₁, А₂, . , А₈ = В.

Ясно, что когда окружность, катясь по прямой а, сделает один оборот, т.е. повернется на 360°, она займет положение (8), а точка С переместится из положения А в положение В.

Если окружность сделает половину полного оборота, т.е. повернется на 180°, она займет положение (4), а точка С переместится в самое верхнее положение С₄.

Если окружность повернется на угол 45°, то окружность переместится в положение (1), а точка С переместится в положение С₁.

На рисунке 1 показаны также другие точки циклоиды, соответствующие оставшимся углам поворота окружности, кратным 45°.

Соединяя плавной кривой построенные точки, получим участок циклоиды, соответствующий одному полному обороту окружности. При следующих оборотах будут получаться такие же участки, т.е. циклоида будет состоять из периодически повторяющегося участка, называемого аркой циклоиды.

Первым, кто стал изучать циклоиду был Галилео Галилей (1564–1642). Он же придумал и ее название.

Циклоида обладает целым рядом замечательных свойств. Упомянем о некоторых из них.

Свойство 1 (Ледяная гора). В 1696 году И.Бернулли поставил задачу о нахождении кривой наискорейшего спуска, или, иначе говоря, задачу о том, какова должна быть форма ледяной горки, чтобы, скатываясь по ней, совершить путь из начальной точки А в конечную точку В за кратчайшее время (рис. 2, а). Искомую кривую назвали «брахистохроной», т.е. кривой кратчайшего времени.

Ясно, что кратчайшим путем из точки A в точку B является отрезок AB . Однако при таком прямолинейном движении скорость набирается медленно и затраченное на спуск время оказывается большим (рис. 2, б).

Скорость набирается тем быстрее, чем круче спуск. Однако при крутом спуске удлиняется путь по кривой и тем самым увеличивается время его прохождения.

Среди математиков, решавших эту задачу, были: Г.Лейбниц, И.Ньютон, Г.Лопиталь и Я.Бернулли. Они доказали, что искомой кривой является перевернутая циклоида (рис. 2, а). Методы, развитые этими учеными при решении задачи о брахистохроне, положили начало новому направлению математики — вариационному исчислению.

Свойство 2 (Часы с маятником). Часы с обычным маятником не могут идти точно, поскольку период колебаний маятника зависит от его амплитуды: чем больше амплитуда, тем больше период. Голландский ученый Христиан Гюйгенс (1629–1695) задался вопросом, по какой кривой должен двигаться шарик на нитке маятника, чтобы период его колебаний не зависел от амплитуды. Заметим, что в обычном маятнике кривой, по которой движется шарик, является окружность (рис. 3,а).

Искомой кривой оказалась перевернутая циклоида. Если, например, в форме перевернутой циклоиды изготовить желоб и пустить по нему шарик, то период движения шарика под действием силы тяжести не будет зависеть от начального его положения и от амплитуды (рис. 3,б). За это свойство циклоиду называют также «таутохрона» – кривая равных времен.

Гюйгенс изготовил две деревянные дощечки с краями в форме циклоиды, ограничивающие движение нити слева и справа (рис. 3,в). При этом сам шарик будет двигаться по перевернутой циклоиде и, таким образом, период его колебаний не будет зависеть от амплитуды.

Из этого свойства циклоиды, в частности следует, что независимо от того, с какого места ледяной горки в форме перевернутой циклоиды мы начнем спуск, на весь путь до конечной точки мы затратим одно и то же время.

Пусть теперь точка закреплена не на окружности, а на продолжении ее радиуса. Если окружность катится по прямой, то эта точка будет описывать кривую, называемую удлиненной циклоидой. Ее построение аналогично построению циклоиды (рис. 4).

Удлиненную циклоиду описывает, например, точка обода колеса железнодорожного вагона.

Отметим, что когда окружность начинает катиться вправо, то закрепленная на продолжении радиуса точка начинает двигаться влево. Поэтому, с какой бы большой скоростью не ехал поезд, в нем в каждый момент времени имеются точки, вектор скорости в которых направлен в противоположную направлению движения сторону.

Траектория движения точки закрепленной на радиусе внутри окружности, катящей по прямой, называется укороченной циклоидой (рис. 5).

По прямой можно катить не только окружность, но и другие геометрические фигуры, например, многоугольники.

Построим траекторию движения точки, закрепленной в вершине правильного треугольника, катящегося по прямой.

Пусть правильный треугольник ABC со стороной a расположен на прямой в положении 1, и точка закреплена в вершине A (рис. 6). Сначала треугольник поворачивается вокруг вершины B на угол 120 ° и занимает положение 2. При этом точка, поворачивается вокруг вершины C и описывает дугу окружности AA ’ , величиной 120 ° и радиусом a . После этого треугольник поворачивается вокруг вершины C ’ на угол 120 ° и занимает положение 3. При этом точка, поворачивается вокруг вершины C ’ и описывает дугу окружности A ’ A ” , величиной 120 ° и радиусом a . Таким образом, одна арка искомой траектории состоит из двух дуг окружности величиной 120 ° и радиусом a .

Построим траекторию движения точки, закрепленной в вершине квадрата, катящегося по прямой.

Пусть квадрат ABCD со стороной a расположен на прямой в положении 1, и точка закреплена в вершине A (рис. 7). Сначала квадрат поворачивается вокруг вершины D на угол 90 ° и занимает положение 2. При этом точка, поворачивается вокруг вершины D и описывает дугу окружности AC , величиной 90 ° и радиусом a . После этого квадрат поворачивается вокруг вершины C ’ на угол 90 ° и занимает положение 3. При этом точка, поворачивается вокруг вершины C ’ и описывает дугу окружности A ’ A ” , величиной 90 ° и радиусом . Далее квадрат поворачивается вокруг вершины B ’ на угол 90 ° и занимает положение 4. При этом точка, поворачивается вокруг вершины B ’ и описывает дугу окружности A ” A ’’’ , величиной 90 ° и радиусом a . Таким образом, одна арка искомой траектории состоит из трех дуг окружностей величиной 90 ° .

Построим траекторию движения точки, закрепленной в вершине правильного шестиугольника, катящегося по прямой.

Пусть правильный шестиугольник ABCDEF со стороной a расположен на прямой, и точка закреплена в вершине A (рис. 8). Сначала шестиугольник поворачивается вокруг вершины F на угол 60 ° . При этом точка, поворачивается вокруг вершины F и описывает дугу окружности AA ’ , величиной 60 ° и радиусом a . После этого шестиугольник поворачивается вокруг вершины E ’ на угол 60 ° . При этом точка, поворачивается вокруг вершины E ’ и описывает дугу окружности A ’ A ” , величиной 60 ° и радиусом . Далее шестиугольник поворачивается вокруг вершины D ’ на угол 60 ° . При этом точка, поворачивается вокруг вершины D ’ и описывает дугу окружности A ” A ’’’ , величиной 60 ° и радиусом 2 a . Затем шестиугольник поворачивается вокруг вершины C ’ на угол 60 ° . При этом точка, поворачивается вокруг вершины C ’ и описывает дугу окружности A ” A ”” , величиной 60 ° и радиусом . Наконец, шестиугольник поворачивается вокруг вершины B ’ на угол 60 ° . При этом точка, поворачивается вокруг вершины B ’ и описывает дугу окружности A ”” A ””’ , величиной 60 ° и радиусом a . Таким образом, одна арка искомой траектории состоит из пяти дуг окружностей величиной 60 ° .

Заметим, что при увеличении числа сторон правильного многоугольника, катящегося по прямой, многоугольник приближается к окружности, а траектория движения точки – к циклоиде. При этом для каждого правильного многоугольника траектория движения точки состоит из дуг окружностей, и касательная в каждой точке перпендикулярна радиусу, соединяющему центр поворота и точку касания. Поэтому касательная в каждой точке циклоиды будет перпендикулярна отрезку, соединяющему нижнюю точку катящейся окружности с данной точкой циклоиды. По-другому, можно сказать, что касательная к циклоиде проходит через вернюю точку катящейся окружности (рис. 9). В частности, касательная к циклоиде в точке A перпендикулярна прямой AB .

Обратим внимание на то, что касательная к циклоиде направлена в ту же сторону, что и направление движения окружности. Поэтому, если велосипедист едет по мокрой дороге, то оторвавшиеся от колеса капли будут лететь не по касательной к колесу, а по касательной к циклоиде и при отсутствии специальных щитков на колесах, могут забрызгивать спину велосипедиста.

Рассмотрим теперь ситуацию, когда окружность катится без скольжения не по прямой, а по другой окружности с внешней стороны. В зависимости от соотношения между радиусами неподвижной и катящейся окружностей будут получаться различные кривые. Построим некоторые из них.

Кривая, которая получается как траектория движения точки, закрепленной на окружности, катящейся с внешней стороны по другой окружности того же радиуса, называется кардиоидой.

Пусть С – точка, закрепленная на окружности, в начальный момент времени находится в положении А (рис. 10). Разделим неподвижную окружность на 8 равных частей точками А₁, А₂, . , А₈ = А.

Ясно, что когда окружность сделает один оборот, т.е. повернется на 360°, она займет исходное положение, и точка С переместится в исходное положение.

Если окружность сделает половину полного оборота, т.е. повернется на 180°, она займет положение (4), а точка С переместится в положение С₄.

Если окружность повернется на угол 45°, окружность переместится в положение (1), а точка С переместится в положение С₁.

На рисунке 10 показаны также другие точки кардиоиды, соответствующие оставшимся углам поворота окружности, кратным 45°.

Соединяя плавной кривой построенные точки, получим кривую, соответствующую одному полному обороту окружности. При следующих оборотах окружности точка С будет описывать ту же самую кривую.

Пусть теперь точка закреплена не на окружности, а на продолжении ее радиуса. Тогда точка будет описывать кривую, называемую удлиненной кардиоидой. Ее построение аналогично построению удлиненной циклоиды (рис. 11).

Траектория движения точки закрепленной на радиусе внутри окружности, называется укороченной кардиоидой (рис. 12).

Рассмотрим теперь ситуацию, когда правильный многоугольник катится по такому же правильному многоугольнику.

Построим траекторию движения точки, закрепленной в вершине правильного треугольника, катящегося по такому же правильному треугольнику.

Пусть правильный треугольник ABC со стороной a расположен в положении 1, и точка закреплена в вершине A (рис. 13). Сначала треугольник поворачивается вокруг вершины C на угол 240 ° и занимает положение 2. При этом точка, поворачивается вокруг вершины C и описывает дугу окружности AA ’ , величиной 240 ° и радиусом a . После этого треугольник поворачивается вокруг вершины B ’ на угол 240 ° и занимает положение 3. При этом точка, поворачивается вокруг вершины B ’ и описывает дугу окружности A ’ A , величиной 240 ° и радиусом a . Таким образом, искомая траектория состоит из двух дуг окружности величиной 240 ° и радиусом a .

Построим траекторию движения точки, закрепленной в вершине квадрата, катящегося по такому же квадрату.

Пусть квадрат ABCD со стороной a расположен на прямой в положении 1, и точка закреплена в вершине A (рис. 14). Сначала квадрат поворачивается вокруг вершины D на угол 180 ° и занимает положение 2. При этом точка, поворачивается вокруг вершины D и описывает дугу окружности AA ’ , величиной 180 ° и радиусом a . После этого квадрат поворачивается вокруг вершины C ’ на угол 180 ° и занимает положение 3. При этом точка, поворачивается вокруг вершины C ’ и описывает дугу окружности A ’ A ” , величиной 180 ° и радиусом . Далее квадрат поворачивается вокруг вершины B ” на угол 180 ° и занимает положение 4. При этом точка, поворачивается вокруг вершины B ” и описывает дугу окружности A ” A , величиной 180 ° и радиусом a . Таким образом, искомая траектория состоит из трех дуг окружностей величиной 180 ° .

Построим траекторию движения точки, закрепленной в вершине правильного шестиугольника, катящегося по такому же шестиугольнику.

Пусть правильный шестиугольник ABCDEF со стороной a расположен на прямой, и точка закреплена в вершине A (рис. 15). Сначала шестиугольник поворачивается вокруг вершины F на угол 120 ° . При этом точка, поворачивается вокруг вершины F и описывает дугу окружности AA ’ , величиной 120 ° и радиусом a . После этого шестиугольник поворачивается вокруг вершины E ’ на угол 120 ° . При этом точка, поворачивается вокруг вершины E ’ и описывает дугу окружности A ’ A ” , величиной 120 ° и радиусом . Далее шестиугольник поворачивается вокруг вершины D ” на угол 120 ° . При этом точка, поворачивается вокруг вершины D ” и описывает дугу окружности A ” A ’’’ , величиной 120 ° и радиусом 2 a . Затем шестиугольник поворачивается вокруг вершины C ”’ на угол 120 ° . При этом точка, поворачивается вокруг вершины C ”’ и описывает дугу окружности A ” A ”” , величиной 120 ° и радиусом . Наконец, шестиугольник поворачивается вокруг вершины B ”” на угол 120 ° . При этом точка, поворачивается вокруг вершины B ”” и описывает дугу окружности A ”” A , величиной 120 ° и радиусом a . Таким образом, искомая траектория состоит из пяти дуг окружностей величиной 120 ° .

Заметим, что при увеличении числа сторон правильного многоугольника, катящегося по прямой, многоугольник приближается к окружности, а траектория движения точки – к кардиоиде. При этом, для каждого правильного многоугольника траектория движения точки состоит из дуг окружностей, и касательная в каждой точке перпендикулярна радиусу, соединяющему центр поворота и точку касания. Поэтому касательная в каждой точке кардиоиды будет перпендикулярна отрезку, соединяющему нижнюю точку катящейся окружности с данной точкой кардиоиды. По-другому, можно сказать, что касательная к кардиоиде проходит через вернюю точку катящейся окружности (рис. 16).

Оказывается, что кардиоида является частным случаем улитки Паскаля (см. Лекцию 3). Это вытекает из следующего свойства кардиоиды.

Если через точку А (рис. 17) провести произвольную прямую и от точки B ее пересечения с неподвижной окружностью отложить в обе стороны отрезки равные диаметру d окружности, то концы этих отрезков С и D будут принадлежать кардиоиде.

Покажем, что точка C принадлежит кардиоиде. Для этого через центр P неподвижной окружности проведем прямую, параллельную AB и отложим на ней отрезок PQ , равный BC (рис. 18). Четырехугольник BCQP – параллелограмм. Поэтому CQ = BP и, следовательно, точка C принадлежит окружности, данного радиуса, касающейся неподвижной окружности в точке R . Осталось доказать, что Ð APR = Ð CQR . Это следует из того, что ACQP – равнобедренная трапеция. Аналогичным образом показывается, что точка D принадлежит кардиоиде.

Легко видеть, что верно и обратное, а именно, если точка C принадлежит кардиоиде, то отрезок AC пересекает неподвижную окружность в точке B , для которой BC равно диаметру этой окружности.

Еще одним свойством кардиоиды является то, что кардиоида есть геометрическое место оснований перпендикуляров, опущенных из точки, расположенной на окружности, на всевозможные касательные к этой окружности.

Действительно, пусть точка A расположена на окружности с центром O (рис. 19), D – какая-нибудь точка окружности. Рассмотрим окружность с диаметром OA . Через точку A проведем прямую, параллельную OD . Обозначим через B точку ее пересечения с окружностью, и отложим отрезок BC , равный радиусу данной окружности. По доказанному выше свойству, точка C принадлежит кардиоиде. Кроме того, так как угол ABO равен 90 ° , четырехугольник OBCD – прямоугольник и, следовательно, CD – касательная к окружности, а AC – перпендикуляр, опущенный из точки A на эту касательную.

Кардиоида относится к классу кривых, называемых эпициклоиды, которые получаются как траектории движения точки, закрепленной на окружности, катящейся внешним образом по другой окружности. При этом радиусы катящейся и неподвижной окружности могут не совпадать.

Рассмотрим, например, случай, когда окружность катится по окружности с внешней стороны и ее радиус в три раза меньше радиуса неподвижной окружности.

Пусть С – точка, закрепленная на окружности, в начальный момент времени находится в положении А (рис. 20). Разделим неподвижную окружность на 12 равных частей.

Ясно, что когда катящаяся окружность пройдет одну треть дуги неподвижной окружности, она сделает один оборот, и точка С переместится в точку C ₄ .

Если окружность пройдет одну шестую дуги неподвижной окружности, то она сделает половину полного оборота, и точка С переместится в положение С₂.

Если окружность пройдет одну двенадцатую часть неподвижной окружности, то она сделает четверть оборота, и точка C переместится в положение C ₁ .

Наконец, если окружность пройдет три двенадцатых дуги неподвижной окружности, то она сделает три четыерти оборота, и точка C переместится в положение C ₃ .

Соединяя плавной кривой построенные точки, получим кривую, соответствующую одному полному обороту окружности. При следующих оборотах окружности точка С опишет еще две такие же кривые, пока не вернется в исходное положение.

На рисунках 21 и 22 показаны укореченная и удлиненная эпициклоиды, соответствующие указанному соотношению радиусов окружностей.

Окружность может катится по другой окружности не только внешним, но и внутренним образом. Соответствующие траектории движения точек называются гипоциклоидами.

В качестве примера гипоциклоиды рассмотрим астроиду – траекторию движения точки закрепленной на окружности, катящейся внутренним образом по другой окружности в четыре раза большего радиуса.

Пусть С – точка, закрепленная на окружности, в начальный момент времени находится в положении А (рис. 23). Разделим неподвижную окружность на 8 равных частей.

Ясно, что когда катящаяся окружность пройдет одну четверть дуги неподвижной окружности, она сделает один оборот, и точка С переместится в точку C ₂ .

Если окружность пройдет одну восьмую дуги неподвижной окружности, то она сделает половину полного оборота, и точка С переместится в положение С₁.

Соединяя плавной кривой построенные точки, получим кривую, соответствующую одному полному обороту окружности. При следующих оборотах окружности точка С опишет еще три такие же кривые, пока не вернется в исходное положение.

На рисунках 24 и 25 показаны укореченная и удлиненная эпициклоиды, соответствующие указанному соотношению радиусов окружностей.

Докажем, что если внутри большой окружности катится окружность вдвое меньшего диаметра, то любая точка внутренней окружности будет двигаться по диаметру внешней окружности.

Пусть окружность повернулась на угол j . Точка C переместилась в положение C ₁ (рис. 26). Тогда угол AOC ₁ равен j /2. С другой стороны, дуги AC и AC ₁ равны. Поэтому Ð AOC = Ð AOC ₁ = j /2. Следовательно, точки O , C ₁ и C лежат на одной прямой, т.е. C ₁ принадлежит диаметру окружности.

На рисунках 27 и 28 показаны эпициклоида и гипоциклоида, соответствующие отношению радиусов окружностей, равном 2/5.

Мы рассмотрели случаи, когда окружность катится по прямой и окружность катится по окружности. Еще одним случаем является случай, когда прямая катится по окружности. На рисунке 29 показана траектория движения точки, закрепленной на прямой, катящейся по окружности против часовой стрелки.

Траектория движения точки, закрепленной на прямой, катящейся по окружности, называется эвольвентой окружности. В домашних условиях ее можно получить следующим образом. Изготовим круг из дерева или фанеры и закрепим его на листе бумаги. Намотаем на него несколько оборотов нити. На конце нити сделаем петлю и проденем в нее острие карандаша. Поставим острие карандаша на бумагу и, удерживая нить в натянутом состоянии, будем перемещать карандаш, разматывая нить. Карандаш будет вычерчивать на бумаге искомую эвольвенту окружности.

Построим эвольвенту правильного треугольника, т.е. траекторию движения точки, закрепленной на прямой, катящейся по правильному треугольнику.

Пусть ABC – правильный треугольник со стороной a , точка закреплена на прямой c в вершине C (рис. 30). Сначала прямая поворачивается вокруг вершины B на угол 120 ° и занимает положение c ₁. При этом точка, поворачивается вокруг вершины B и описывает дугу окружности CC ₁ , величиной 120 ° и радиусом a . После этого прямая поворачивается вокруг вершины A на угол 120 ° и занимает положение c ₂ . При этом точка, поворачивается вокруг вершины A и описывает дугу окружности C ₁ C ₂ , величиной 120 ° и радиусом 2 a . Затем прямая поворачивается вокруг вершины C на угол 120 и занимает положение c ₃ = c . При этом точка, поворачивается вокруг вершины C и описывает дугу окружности C ₂ C ₃ , величиной 120 ° и радиусом 3 a и так далее.

Построим эвольвенту квадрата, т.е. траекторию движения точки, закрепленной на прямой, катящейся по квадрату.

Пусть ABCD – квадрат со стороной a , точка закреплена на прямой c в вершине A (рис. 31). Сначала прямая поворачивается вокруг вершины B на угол 90 ° и занимает положение c ₁. При этом точка, поворачивается вокруг вершины B и описывает дугу окружности CC ₁ , величиной 90 ° и радиусом a . После этого прямая поворачивается вокруг вершины A на угол 90 ° и занимает положение c ₂ . При этом точка, поворачивается вокруг вершины A и описывает дугу окружности C ₁ C ₂ , величиной 90 и радиусом 2 a . Затем прямая поворачивается вокруг вершины D на угол 90 ° и занимает положение c ₃ . При этом точка, поворачивается вокруг вершины D и описывает дугу окружности C ₂ C ₃ , величиной 90 ° и радиусом 3 a и так далее.

Заметим, что при увеличении числа сторон правильного многоугольника, по которому катится прямая, многоугольник приближается к окружности, а траектория движения точки – к эвольвенте окружности. При этом для каждого правильного многоугольника траектория движения точки состоит из дуг окружностей, и касательная в каждой точке перпендикулярна радиусу, соединяющему центр поворота и точку касания. Поэтому касательная в каждой точке эвольвенты окружности также будет перпендикулярна прямой, проходящей через эту точку и касающейся окружности.

Задачи для самостоятельного решения

1. Окружность радиуса 3 см катится по прямой. Нарисуйте соответствующую циклоиду.

2. Имеет ли циклоида: а) оси симметрии; б) центр симметрии?

Ответ: а) Да; б) нет.

3. Укажите точки на циклоиде, касательные в которых наклонены к прямой под углом 45 ° .

Ответ. Точки циклоиды, удаленные от прямой на расстояние радиуса окружности.

4. Окружность радиуса 3 см катится с внешней стороны по другой окружности того же радиуса. Нарисуйте соответствующую кардиоиду.

5. Имеет ли кардиоида: а) оси симметрии; б) центр симметрии?

Ответ: а) Да; б) нет.

6. Окружность радиуса 1 см катится с внутренней стороны по другой окружности радиуса 4 см. Нарисуйте соответствующую астроиду.

7. Имеет ли астроида: а) оси симметрии; б) центр симметрии?

8. Нарисуйте кривую, получающуюся как траектория движения точки, закрепленной на окружности радиуса 1 см, катящейся с внешней стороны по окружности радиуса 2 см.

9. Нарисуйте кривую, получающуюся как траектория движения точки, закрепленной на окружности радиуса 2 см, катящейся с внутренней стороны по окружности радиуса 6 см.

10. Нарисуйте эпициклоиду и гипоциклоиду с отношением радиусов катящейся и неподвижной окружности, равным 3/5.

11. Какое отношение радиусов катящейся и неподвижной окружности для кривых, изображенных на рисунке 32, 33?

12. Нарисуйте траекторию движения точки, закрепленной на окружности, катящейся с внешней стороны по правильному треугольнику со стороной, равной: а) длине окружности; б) половине длины окружности.

13. Нарисуйте траекторию движения точки, закрепленной на окружности, катящейся с внешней стороны по квадрату со стороной, равной: а) длине окружности; б) половине длины окружности.

14. Нарисуйте траекторию движения точки, закрепленной в вершине правильного треугольника, катящегося с внешней стороны по окружности, длина которой равна периметру треугольника.

1. Березин В. Кардиоида //Квант. – 1977. № 12.

2. Берман Г.Н. Циклоида. – М.: Наука, 1975.

3. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. – 3-е изд. – М.: МЦНМО, 2000.

4. Веров С. Тайны циклоиды //Квант. – 1975. № 8.

5. Веров С. Брахистохрона, или еще одна тайна циклоиды //Квант. – 1975. № 12.

6. Маркушевич А.И. Замечательные кривые. – М.- Л.: Гос. изд. течн. – теор. лит., 1951. — / Популярные лекции по математике, выпуск 4.

7. Савелов А.А. Плоские кривые. – М.: ФИЗМАТЛИТ, 1960.

8. Смирнова И.М., Смирнов В.А. Геометрия 7-9. Учебник для общеобразовательных учреждений. – М.: Мнемозина, 2005.