Параллельные прямые в кубе

10 класс. Геометрия. Параллельные прямые в пространстве.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

1. Тема и цели урока

Мы уже изучали параллельные прямые в планиметрии. Теперь нужно дать определение параллельных прямых в пространстве и доказать соответствующие теоремы.

Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

2. Определение параллельных прямых в пространстве

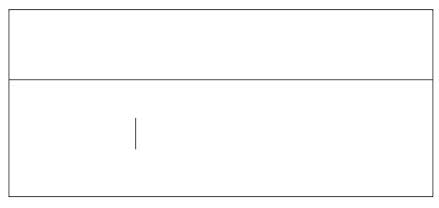
Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются (Рис. 1.).

Обозначение параллельных прямых: a || b.

Видео:Параллельность прямых. Практическая часть. 10 класс.Скачать

3. Теорема 1 и ее доказательство

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Дано: прямая а, (Рис. 2.)

Доказать: существует единственная прямая b || a,

Через прямую а и точку , не лежащую на ней, можно провести единственную плоскость α (Рис. 3.). В плоскости α можно провести единственную прямую b, параллельную а, проходящую через точку M (из аксиомы планиметрии о параллельных прямых). Существование такой прямой доказано.

Докажем единственность такой прямой. Предположим, что существует другая прямая с, проходящая через точку M и параллельная прямой а. Пусть параллельные прямые а и с лежат в плоскости β. Тогда плоскость β проходит через точку M и прямую а. Но через точку M и прямую а проходит единственная плоскость (в силу теоремы 2). Значит, плоскости β и α совпадают. Из аксиомы параллельных прямых, следует, что прямые b и с совпадают, так как в плоскости существует единственная прямая, проходящая через данную точку и параллельная заданной прямой. Единственность доказана.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

4. Лемма (о двух параллельных прямых, пересекающих плоскость) и ее доказательство

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Дано: а || b,

Доказать:

Доказательство: (Рис. 4.)

Существует некоторая плоскость β, в которой лежат параллельные прямые а и b. Точка М принадлежит и плоскости α, и прямой а, которая лежит в плоскости β. Значит, М – общая точка плоскостей α и β. А по третьей аксиоме, существует прямая MN, по которой пересекаются эти две плоскости.

Прямая MN пересекается с прямой b.(так как в противном случае, получается, что прямые MN и b параллельные, то есть a = MN, что невозможно, так как прямая а пересекается с плоскостью α в точке М по условию). То есть точка N – это точка пересечения прямой b и плоскости α..

Докажем, что N — это единственная общая точка прямой b и плоскости α. Допустим, что есть другая точка, но тогда прямая bпринадлежит плоскости α (по второй аксиоме). То есть MN = b, что невозможно, так как прямые а и bпараллельны, а прямая а должна пересекаться с прямой MN. Лемма доказана.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

5. Теорема 2 и ее доказательство

Если две прямые параллельны третьей, то они параллельны.

Дано:

Доказать: .

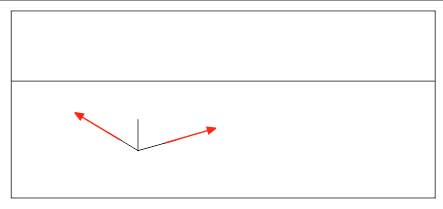
Доказательство: (Рис. 5.)

Выберем произвольную точку К на прямой b. Тогда существует единственная плоскость α, проходящая черезточку К и прямую а. Докажем, что прямая bлежит в плоскости α.

Предположим противное. Пусть прямая bне лежит в плоскости α. Тогда прямая bпересекает плоскость α в точке К. Так как прямые bи с параллельны, то, согласно лемме, прямая с также пересекает плоскость α. Прямые а и с также параллельны, значит, по лемме, прямая а также пересекает плоскость α, но это невозможно, так как прямая а лежит в плоскости α. Получили противоречие. То есть, предположение было неверным, а значит, прямая bлежит в плоскости α.

Докажем, что прямые а и b не пересекаются. Предположим противное. Пусть прямые а и bпересекаются в некоторой точке М. Но тогда получается, что через точку М проходят две прямые а и b, параллельные прямой с, что невозможно в силу теоремы 1. Получили противоречие. Значит, прямые а и b не пересекаются.

Мы доказали, что прямые а и b не пересекаются и что существует плоскость α, в которой лежат прямые а и b. Значит, прямые а и bпараллельны (по определению), что и требовалось доказать.

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

6. Итоги урока

Итак, мы дали определение параллельных прямых и доказали теорему о параллельных прямых в пространстве. Также мы доказали важную лемму о пересечении параллельными прямыми плоскости и с помощью этой леммы доказали теорему: если две прямые параллельны третьей, то они параллельны. Эта теория будет использоваться дальше и для доказательства других теорем, и для решения задач.

Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

Куб — свойства, виды и формулы

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Периметр куба

Сумма длин всех рёбер равна:

Видео:Параллельные прямыеСкачать

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Видео:Скрещивающиеся прямыеСкачать

Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

Видео:Готовимся к ЕГЭ. Стереометрия. Базовые задачи. Угол между прямыми. КубСкачать

Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

Видео:10 класс - Геометрия - Скрещивающиеся прямыеСкачать

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Видео:Как строить сечение куба? Стереометрия. 10-11 класс | Математика | TutorOnlineСкачать

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

у куба все грани равны, являются квадратами;

у куба все рёбра равны;

один центр и несколько осей симметрии.

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Урок 3. Линейная перспектива. Построения, часть 1.

Без знания законов линейной перспективы невозможно реалистично изобразить ни один объемный предмет, будь то человек или табуретка.

Но пугаться не стоит. Несмотря на громкое название, основных законов всего два и запомнить их очень просто.

Все вы когда-нибудь ездили на электричке и переходя железнодорожные пути, смотрели не идет ли поезд. Что вы видели в этот момент?

Сходящие на линии горизонта рельсы, очевидно, параллельные друг другу.

И одинаковой высоты столбы линии электропередач, ближний из которых кажется значительно больше дальнего.

Собственно, это и есть два основных закона линейной перспективы:

1. Параллельные прямые, удаляющиеся от нас мы видим сходящимися в одной точке. Эта точка называется точкой схода. Она, или ее проекция находится на линии горизонта
2. Предметы одинаковой величины кажутся тем меньше, чем дальше от нас они расположены.

Видео:Сечение Куба. Параллельные переносыСкачать

Основные понятия перспективы.

Перед тем, как мы начнем применять эти законы на практике, я дам вам несколько определений. Это упростит объяснения и поможет вам легче понимать специальную литературу.

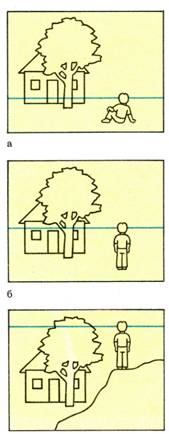
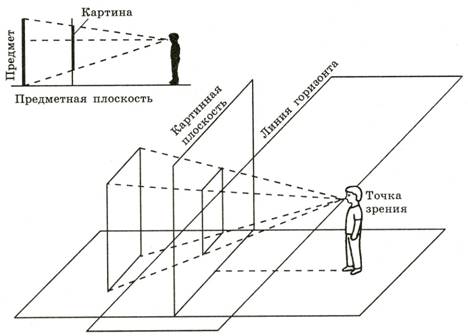
Горизонт ( линия горизонта) — плоскость, горизонтальная, бесконечная, находящаяся на высоте глаз наблюдателя и ВСЕГДА видимая в виде прямой горизонтальной линии.

Условно можно считать, что перспективный горизонт и горизонт географический в нашем зрении совпадают.

Все предметы, находящиеся ниже этой плоскости, ниже горизонта, мы видим сверху; все предметы, находящиеся выше горизонта,- видим снизу.

Важно запомнить, что линия горизонта всегда находится на уровне ваших глаз. Если вы сядете на землю, то перспективный горизонт опустится вместе с вами, при подъеме в гору он поднимается.

Точка зрения – условное расположение взгляда художника относительно изображаемого объекта.

Картинная плоскость — условная плоскость, на которую проецируется изображение. Она всегда вертикальна. Независимо от того, как расположен ваш лист.

Сокращения. Если поверхность находится под углом к картинной плоскости, она нам кажется более узкой, чем когда она параллельна картинной плоскости. Этот эффект называется — сокращения. Чем ближе угол между плоскостями к 90 градусам, тем больше сокращения. Если угол равен 90 градусам, мы видим поверхность, как линию.

Видео:Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

Основные понятия. Тест.

Чтобы закрепить полученные знания, предлагаю вам пройти небольшой тест. Ответы присылайте, пожалуйста, мне в личном сообщении.

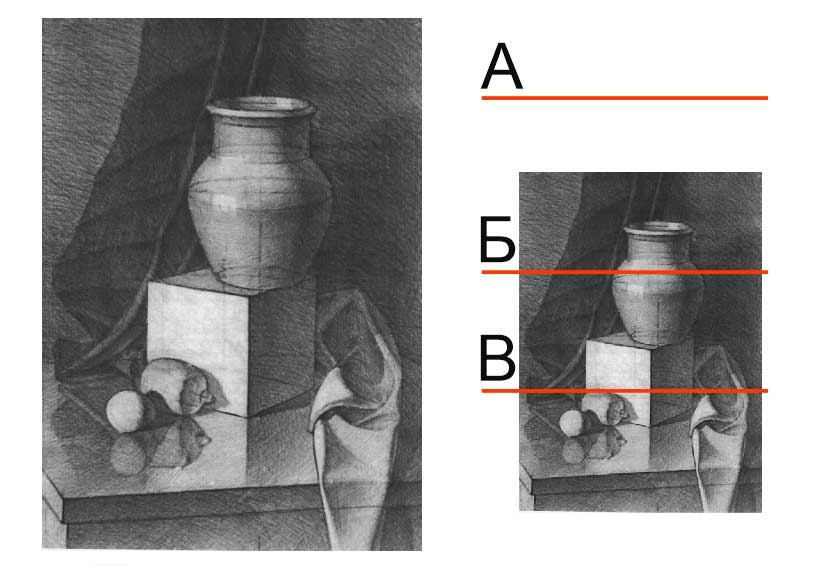
1. Где находится линия горизонта на картине.
   1. А
   2. Б
   3. В
   4. В натюрморте ее нет, горизонт виден только в пейзаже.
2. Картинная плоскость…
   1. … всегда совпадает с плоскостью листа, на котором вы работаете.
   2. … может совпадать, если лист расположен вертикально и прямо перед вами.
   3. … никогда не совпадает.
3. Геометрические тела в натюрморте находятся …
   1. … на линии горизонта.
   2. … выше линии горизонта.
   3. … ниже линии горизонта.
   4. … и выше и ниже.

Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Перспектива с одной точкой схода.

Один из двух наиболее распространенных типов перспективных построений. Мы ее используем, когда рисуем объект с прямыми углами, передняя сторона которого параллельна картинной плоскости. Этот тип построений часто используется для изображений интерьеров и архитектуры.

Saint Jerome in His Study Albrecht Dürer 1514

Видео:24. Параллельные линии могут пересекаться. Такое возможно?Скачать

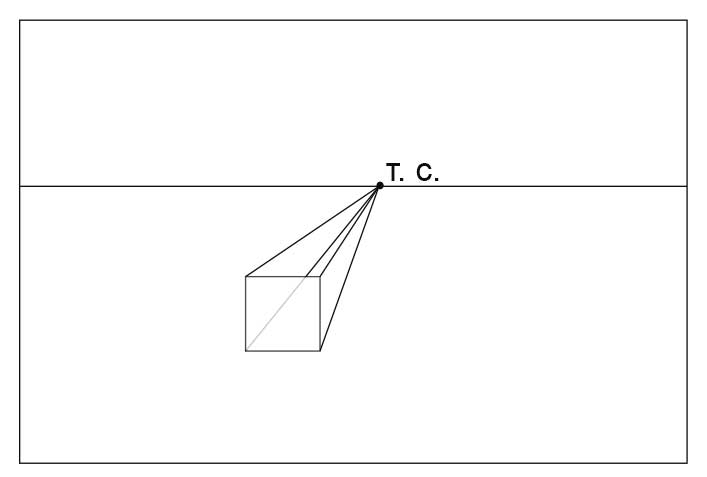
Разберем построения перспективы с одной точкой схода на примере построения куба.

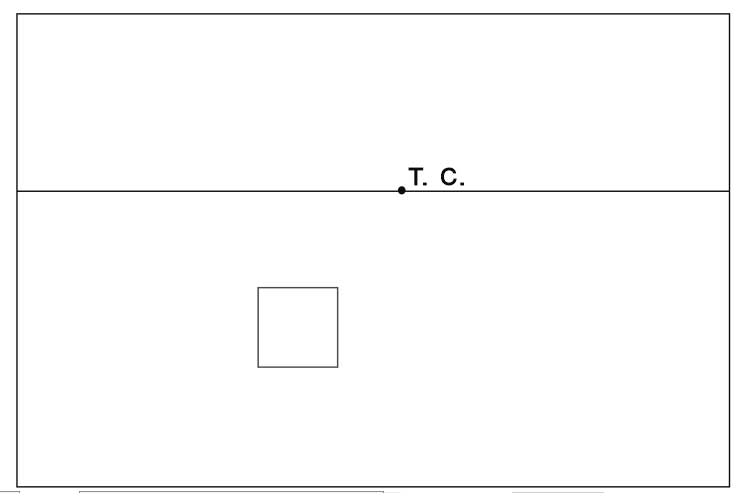
• Нарисуем на нашем листе линию горизонта. Местоположение выбираем произвольно, лучше в середине или верхней трети листаю
• Нарисуем переднюю сторону куба, ниже линии горизонта.Она будет видна нам без искажений, то есть как квадрат.

• Зададим точку схода (Т.С.) на линии горизонта. Когда мы рисуем по воображению, мы ее задаем произвольно. При натурном рисовании, она зависит от нашей точки зрения и определяется по параллельным прямым в изображаемом объекте.

• Уходящие от нас ребра куба параллельны друг другу, а значит сходятся на линии горизонта в точке схода. Проведем прямые из углов передней стороны куба в точку схода.

• Определим на глаз длину уходящих от нас ребер куба. Мы видим их в сокращении. Справа от рисунка показаны ошибка при определении длины.

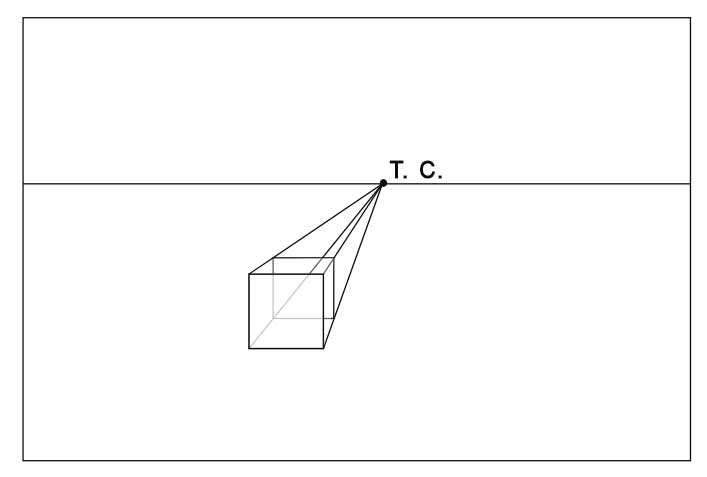
• Достраиваем дальнюю сторону куба. Обратите внимание, что она тоже видна нам без искажений, то есть, как квадрат.

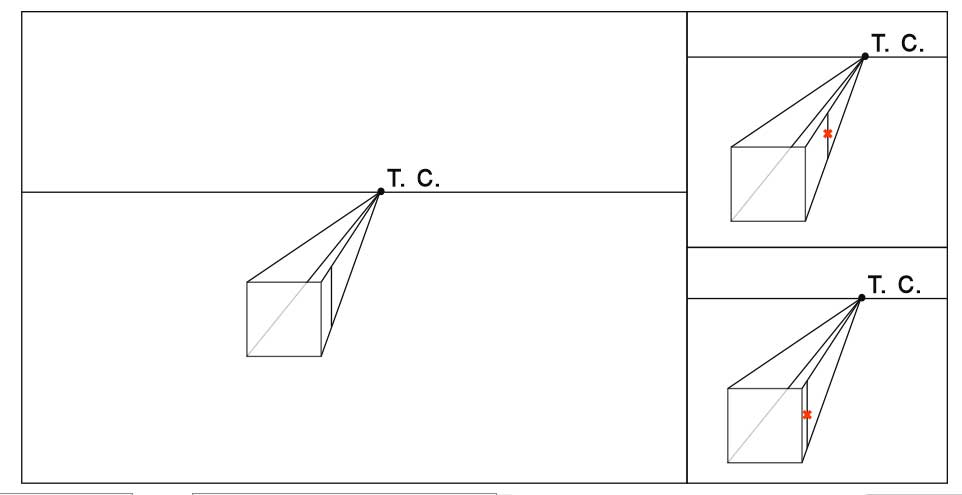
Упражнение 1.

Постройте кубы на линии горизонта и выше нее.

Дополнительное упражнение 1.

Распечатайте работы, восстановите построение и найдите, где проходит линия горизонта.

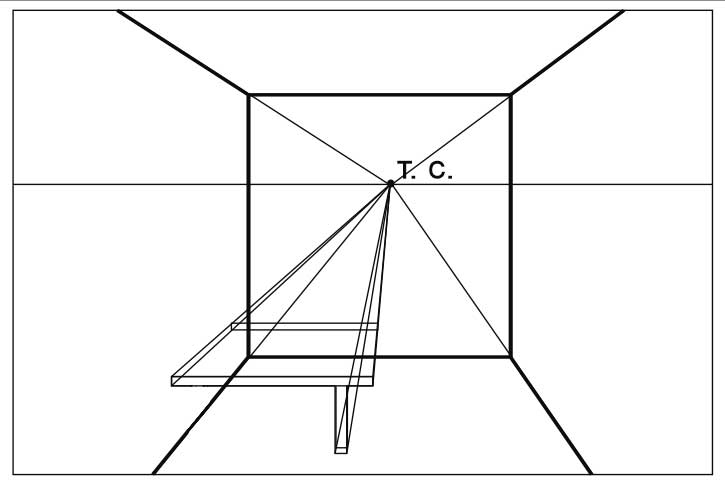
Дополнительное упражнение 2.

Постройте недостающие ножки у стола.

Перспектива с двумя точками схода.

Это более распространенный тип перспективных построений. Мы им пользуемся тогда, когда изображаем объекты, стороны которых расположены под прямым углом друг к другу. Сами эти объекты могут находиться под произвольными углом к картинной плоскости.

Обратите внимание, что несмотря на название типа построения, на одной работе точек схода может быть бесконечно много. Потому что для каждой группы параллельных прямых точка схода своя. Если у вас на работе несколько предметов, расположенных под разным углом к картинной плоскости, групп параллельных прямых тоже будет несколько.

View of Warsaw from the Terrace of the Royal Castle
Bernardo Bellotto1773

В одной работе могут совмещаться построение перспективы с одной и с двумя точками схода.

В системах построения с одной и с двумя точками схода мы условно считаем все вертикали строго вертикальны. Мы не учитываем, что вы смотрите на объект сверху или снизу и, соответственно, один из его краев ближе к вам, а вертикальные грани являются параллельными прямыми, удаляющимся от вас и должны иметь точку схода. Если вы хотите учитывать этот фактор, вам нужно использовать систему построения с тремя точками схода. Но о ней и о других системах построения объемных изображений мы будем говорить в следующем курсе.

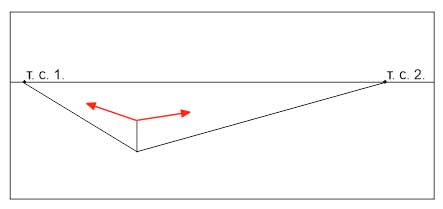
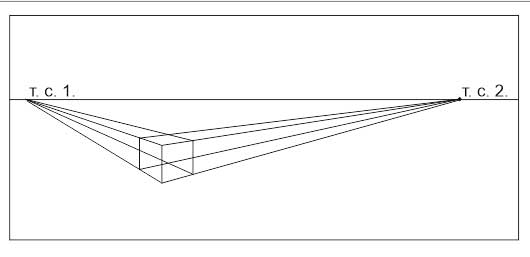
Разберем построения перспективы с двумя точками схода на примере куба.

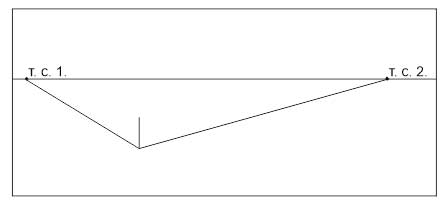
• Проводим линию горизонта по центру листа или чуть выше.
• Произвольно задаем длину переднего вертикального ребра куба.

• Задаем направления горизонтальных, уходящих от нас, ребер куба. Углы выбираем произвольно, но стараемся, чтобы визуально угол между ребрами читался как прямой. (Он не будет прямым в геометрическом смысле, так как он находится не в плоскости, параллельной картинной, и мы видели его с перспективными искажениями)

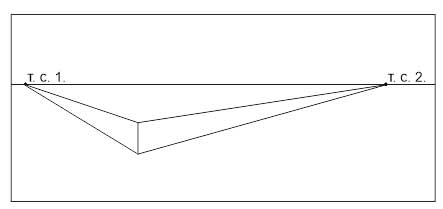
• Продлеваем горизонтальные ребра до линии горизонта. На пересечении получаем две точки схода (Т.С1 и Т.С.2).

• От верхнего края переднего ребра проводим линии в точки схода.

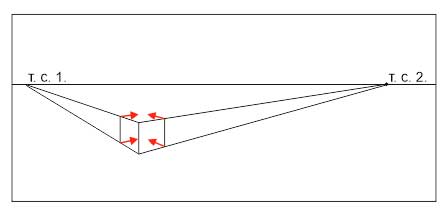
• На глаз определяем ширину боковых сторон куба. Обратите внимание, что их ширина будет меньше высоты, так как мы видим ее в сокращении, а высоту- нет. Чем на вашем рисунке меньше угол между горизонтальным и вертикальным ребром, тем уже соответствующая сторона.

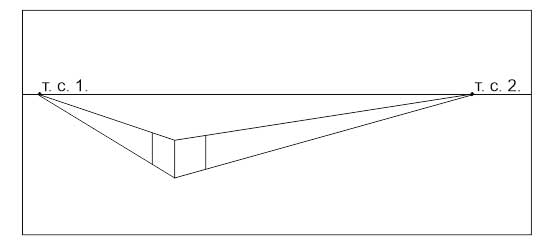
• От дальних углов боковых поверхностей проводим линии в точки схода.

• На пересечении получаем верх и низ дальнего вертикального ребра. Соединяем их — строем ребро.

Упражнение 2.

Постройте кубы на и выше линии горизонта с теми же точками схода.

Задание. Воображаемый интерьер.

То, что окружает человека иногда говорит о нем больше, чем его внешность. Мне бы хотелось, чтобы вы придумали интерьер «с характером»: пространство, глядя на которое понимаешь, кто там обитает или что там произошло. Хотя ни обитателей ни событий мы не видим.

Как примеры тем предлагаю:

» комната, где прячется преступник»

«комната одинокого человека»

«комната, где находят ответы на вопросы»

Если вы боитесь не справиться с интерьером, можно взять упрощённый вариант задания — предмет мебели, по которому можно узнать владельца, Например: » любимое кресло старого профессора». Можно пофантазировать на тему любимых предметов мебели литературных героев.

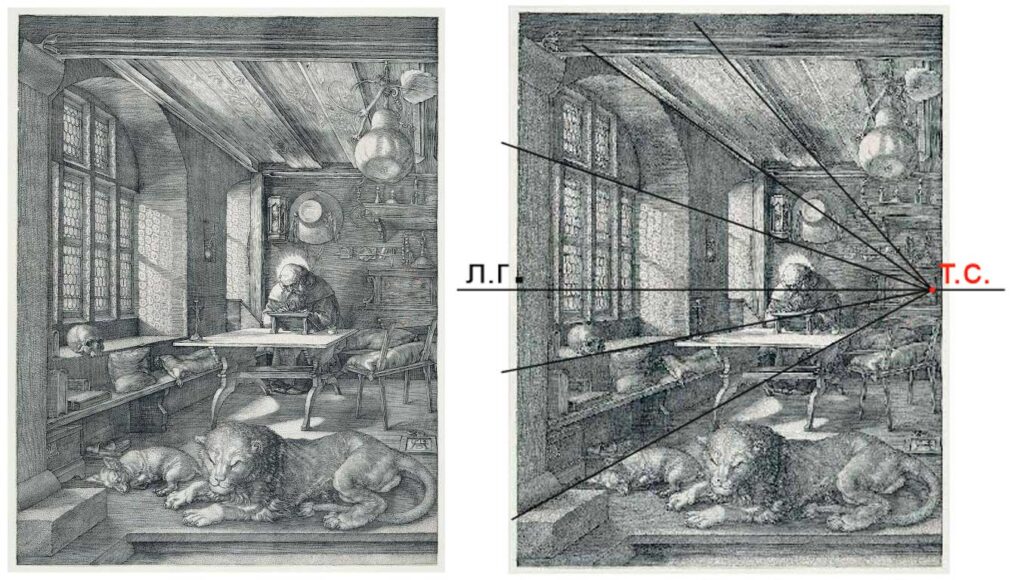
Дополнительное упражнение 3.

Даже мастера путались в построениях.

Распечатайте картины, восстановите линии построения и найдите, где ошиблись художники.

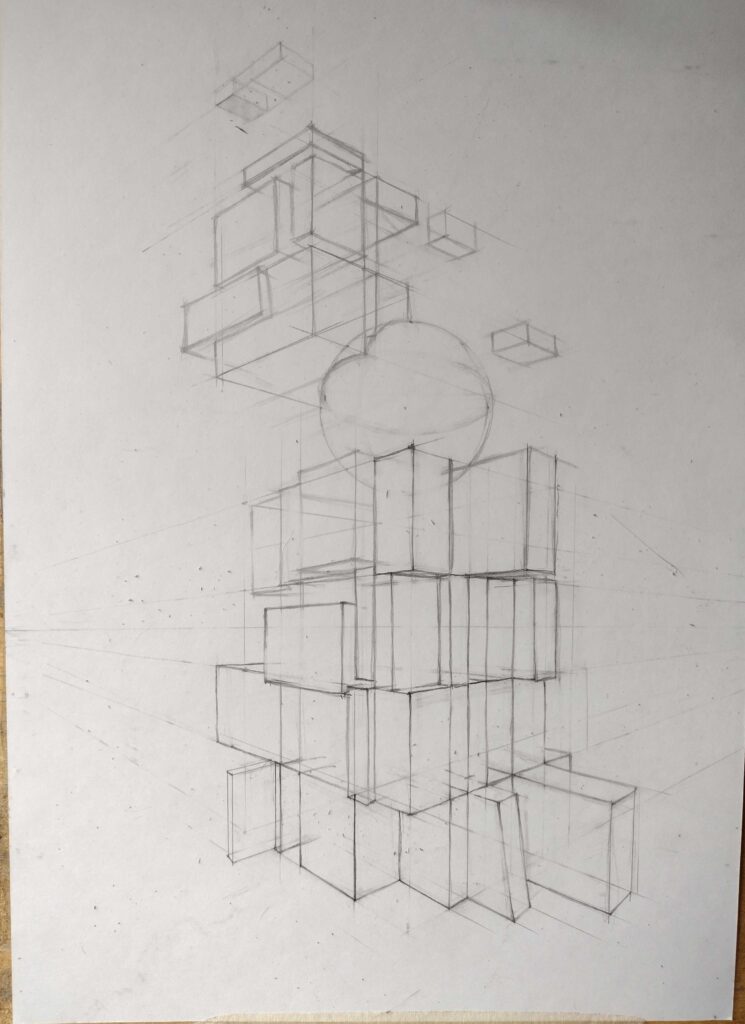
Дополнительное задание.

Композиция из геометрических тел. Линейный рисунок без тона. Основные элементы строим напросвет( так, как будто они из стекла) Стараемся пока использовать только кубы или прямоугольные параллелепипеды.

Кубы построены напросвет

Предлагаю вам вообразить себя архитектором или скульптором-абстракционистом и придумать интересную и эстетичную конструкцию из геометрических тел. Вы можете создать просто гармоничную структуру или попробовать изобразить абстрактное понятие, например, тяжесть или легкость, величие, власть или угрозу. Любые, даже самые необычные варианты, приветствуются.