Среди аксиом Евклида была аксиома о параллельности прямых, а точнее, пятый постулат о параллельных линиях : если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которых меньше развернутого угла, то такие прямые пересекаются при достаточном продолжении с одной стороны. В современной формулировке она говорит о существовании не более одной прямой, проходящей через данную точку вне данной прямой и параллельной этой данной прямой.
Сложность формулировки пятого постулата породила мысль о возможной зависимости его от других постулатов, и потому возникали попытки вывести его из остальных предпосылок геометрии. Как правило, это заканчивалось неудачей. Были попытки доказательства от противного: прийти к противоречию, предполагая верным отрицание постулата. Однако и этот путь был безуспешным.
Наконец, в начале XX века почти одновременно сразу у нескольких математиков: у К. Гаусса в Германии, у Я. Больяи в Венгрии и у Н. Лобачевского в России возникла мысль о существовании геометрии, в которой верна аксиома: на плоскости через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную.
В силу приоритета Н. Лобачевского, который первым выступил с этой идеей в 1826, и его вклада в развитие новой, отличной от евклидовой геометрии последняя была названа в его честь «геометрией Лобачевского».
Аксиоматика планиметрии Лобачевского отличается от аксиоматики планиметрии Евклида лишь одной аксиомой: аксиома параллельности заменяется на ее отрицание – аксиому параллельности Лобачевского
Найдутся такая прямая и такая не лежащая на ней точка , что через проходят по крайней мере две прямые, не пересекающие .
Как уже отмечалось в § 15.1, непротиворечивость системы аксиом доказывается представлением модели, в которой реализуются данные аксиомы. Модель планиметрии Лобачевского на евклидовой плоскости, которая будет здесь представлена, сделана по материалам учебника «Геометрия» (А. Д. Александров, А. Л. Вернар, В. И. Рыжик, М: Просвещение, 1991). Эта модель была предложена французским математиком Анри Пуанкаре в 1882 году.
Для начала напомним основные понятия и аксиоматику, на которой базировалось изложение, систематизировав их заново и дополнив необходимыми аксиомами.
За основные объекты были приняты точка, прямая и фигура. За основные отношения между этими объектами принимаются:
1) точка принадлежит фигуре, в частности прямой;
2) точка лежит между двумя точками для точек прямой.
Следующие определения базируются на основных определениях.
- Фигура называется объединением некоторых данных фигур, если ей принадлежат все точки этих фигур, и никакие другие.
- Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными ее точками. Эти точки называются концами отрезка.
- Лучом называется часть прямой, состоящая из всех ее точек, лежащих по ту же сторону от точки , что и точка . Точка называется вершиной луча.
- Углом называется фигура, которая состоит из точки – вершины угла и двух различных лучей, исходящих из этой точки, – сторон угла.
- Полуплоскостью, ограниченной прямой , называется фигура, обладающая следующими свойствами:
- она не содержит прямую ;
- если точки и принадлежат полуплоскости, то отрезок не имеет общих точек с ;
- если же принадлежит полуплоскости, а нет, то отрезок имеет общую точку с прямой .
Приведем систему аксиом, обозначив римской цифрой номер группы, а арабской – номер аксиомы в группе.
I. Аксиомы связи прямой и точки.
- Существуют, по крайней мере, две точки.
- Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
- Через любые две точки можно провести прямую и только одну.
- Из трех точек на прямой одна и только одна лежит между двумя другими.
II. Метрические аксиомы отрезка.
- Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
- На каждом луче от его начала можно отложить отрезок заданной длины и только один.
III. Аксиома непрерывности.
Пусть и – любые две точки прямой и пусть 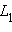
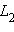
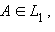
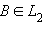
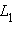
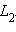
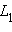
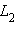
IV. Аксиомы плоскости.
- Прямая разбивает плоскость на две полуплоскости.
- Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
- От любого луча в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
- Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данного луча.
V. Аксиома параллельности Евклида.
Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Построение модели Пуанкаре начнем с того, что придадим конкретный смысл основным объектам и основным отношениям планиметрии Лобачевского. Для этого фиксируем на евклидовской плоскости горизонтальную прямую . Она носит название «абсолюта». Точками плоскости Лобачевского считаются точки плоскости , лежащие выше абсолюта . Таким образом, в модели Пуанкаре плоскость Лобачевского – это полуплоскость , лежащая выше абсолюта.
Прямыми плоскости считаются полуокружности с центрами на абсолюте или лучи с вершинами на абсолюте и перпендикулярные ему.
Фигура на плоскости Лобачевского – это фигура полуплоскости . Принадлежность точки фигуре понимается так же, как и на евклидовой плоскости . При этом отрезком плоскости считается дуга окружности с центром на абсолюте или отрезок прямой, перпендикулярной абсолюту (см. рис. 15.2.1). Точка лежит между точками и , значит, что принадлежит дуге . В условиях нашей модели это эквивалентно тому, что лежит между и , где , и – проекции точек , и соответственно на абсолют. Чтобы ввести понятие равенства неевклидовых отрезков в модели Пуанкаре, определяют неевклидовы движения в этой модели.
Неевклидовым движением называется преобразование , которое является композицией конечного числа инверсий с центрами на абсолюте и осевых симметрий плоскости , оси которых перпендикулярны абсолюту. Инверсии с центром на абсолюте и осевые симметрии плоскости , оси которых перпендикулярны абсолюту, называют неевклидовыми симметриями. Два неевклидовых отрезка называют равными, если один из них неевклидовым движением можно перевести во второй.
Свойства неевклидовых движений.
- Суперпозиция неевклидовых движений есть снова неевклидово движение. Это вытекает непосредственно из определения неевклидова движения.
- При неевклидовых движениях образами неевклидовых отрезков, прямых, лучей и углов являются соответственно неевклидовы отрезки, прямые, лучи и углы. Это свойство вытекает из свойств инверсии и свойств евклидовой осевой симметрии. Необходимо отметить, что неевклидовы углы, преобразующиеся друг в друга неевклидовым движением, равны в смысле приведенного ранее определения, и их величины (в евклидовом смысле) также равны.
- Если неевклидово движение переводит неевклидов луч в себя, то либо это тождественное преобразование, либо неевклидова осевая симметрия относительно неевклидовой прямой, содержащей данный луч. В обоих случаях все точки этой прямой для данного преобразования неподвижны. Это свойство дается без доказательства.
Выше дана реализация всех основных понятий аксиоматики планиметрии Лобачевского через понятия евклидовой геометрии. Теперь необходимо проверить справедливость приведенных выше аксиом.
Из группы аксиом I очевидна справедливость аксиом I.1, I.2, I.4.
Пусть даны точки и .
Прямая (евклидова) не перпендикулярна к абсолюту (рис. 15.2.2). Тогда серединный перпендикуляр отрезка пересекает абсолют в некоторой точке . Так как по построению = , то полуокружность окружности с центром в точке и радиусом , лежащая выше абсолюта, является неевклидовой прямой, содержащей точки и . Эта прямая (неевклидова) единственна, так как на абсолюте есть лишь одна точка, равноудаленная от точек и , – это точка .
Так как каждый неевклидов отрезок представляет из себя либо евклидов отрезок (если прямая перпендикулярна абсолюту), либо дугу окружности, то в первом случае аксиома выполнена очевидно.
Для анализа второго случая допустим, что есть искомый неевклидов отрезок. Рассмотрим инверсию относительно окружности с центром в точке , пересечения неевклидовой прямой и абсолюта и радиусом , равным (рис. 15.2.4). При этом образом невклидовой прямой будет луч 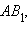
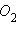
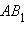
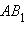
Возможны несколько случаев.
Пусть неевклидов луч представляет из себя луч евклидовой прямой, который не имеет точки пересечения с абсолютом (рис. 15.2.5). Тогда выполнение аксиомы следует из ее справедливости для евклидова луча.
Пусть неевклидов луч представляет из себя часть евклидовой прямой, перпендикулярной абсолюту и ограниченной началом луча (включая точку ) и точкой , лежащей на абсолюте (рис. 15.2.6).
Сделаем преобразование инверсии относительно окружности с центром в точке и радиусом . По свойствам инверсии отрезок преобразуется в луч евклидовой прямой с началом в точке . В соответствии с аксиомой II.2 на полученном луче от его начала можно отложить отрезок заданной длины и только один. Пусть – конец этого отрезка. Тогда ее прообразом при инверсии является некоторая точка 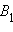
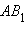
Неевклидов луч – дуга полуокружности, содержащая точку – начало луча, и не содержащая точку , точку пересечения полуокружности с абсолютом (рис. 15.2.7). Как и в случае рассмотрения аксиомы II.1, сделаем преобразование инверсии относительно окружности с центром в точке и радиусом . Образом неевклидова луча будет луч евклидовой прямой, перпендикулярной абсолюту. На этом луче можно отложить отрезок данной длины и только один. Пусть – конец этого отрезка. Далее обоснование дословно повторяет обоснование, приведенное в предыдущем пункте.
Аксиома непрерывности III для неевклидовых отрезков сводится к случаю евклидовых отрезков проектированием на абсолют (рис. 15.2.8) или преобразованием неевклидова отрезка в отрезок евклидовой прямой, перпендикулярной абсолюту, с помощью инверсии, описанной при доказательстве справедливости аксиомы II.1. В модели Пуанкаре выполняется аксиома IV.1. Неевклидовы полуплоскости изображены на рис. 15.2.9. Неевклидов отрезок, соединяющий две точки неевклидовой полуплоскости, не пересекает ее границы. Действительно, предположив противное, мы пришли бы к тому, что евклидовы окружности пересекались бы в четырех точках (рис. 15.2.10), что невозможно.
Возможные реализации углов в модели Пуанкаре для неевклидовых углов показаны на рис. 15.2.11.
Из рисунка видно, что неевклидовыми углами являются угол между пересекающимися окружностями, а также между окружностью и пересекающей ее прямой. В соответствии с определением, данным в разделе 13, угол между пересекающимися окружностями это – угол между касательными к ним прямыми, проведенными в точке пересечения, а угол между окружностью и пересекающей ее прямой – это угол между касательной к окружности в точке пересечения и прямой.
Таким образом величины неевклидовых углов определяются через величины соответствующих евклидовых углов. Отсюда достаточно очевидна справедливость аксиомы IV.2.
Пусть неевклидовым лучом с вершиной является часть полуокружности (рис. 15.2.13) с центром в точке на абсолюте.
Проведем касательную к полуокружности в точке и отложим от луча угол, равный данному, в полуплоскость, не содержащую данную полуокружность. Пусть – вторая сторона угла. Восстановим перпендикуляр к лучу в точке . Если этот перпендикуляр пересекает абсолют в точке , то, построив полуокружность с центром в точке и радиусом, равным , получим две пересекающиеся в точке полуокружности, угол между которыми равен по построению. Если же перпендикуляр не пересекает абсолют, т. е. он параллелен абсолюту или, что то же самое, луч перпендикулярен , то второй стороной неевклидова луча является искомый евклидов луч . Единственность такого угла следует из справедливости аксиомы для евклидовой плоскости.
Проверку аксиомы IV.4 проведем только для случая, когда данный неевклидов луч есть часть полуокружности.
В соответствии с аксиомами II.2 и IV.3 отложим от вершины данного луча отрезок 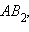
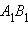
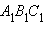
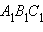
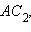
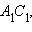
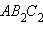
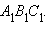
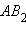
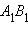
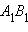
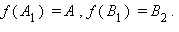
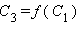
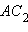
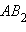
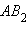
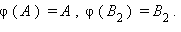
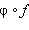
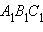
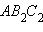
Утверждение аксиомы параллельности Лобачевского выполняется не только для некоторой прямой и некоторой точки , не лежащей на , но и для любой неевклидовой прямой и любой не лежащей на ней точки (рис. 15.2.14).
Приведенное выше рассмотрение позволяет сделать вывод о непротиворечивости геометрии Лобачевского и обосновать независимость аксиомы параллельности от остальных аксиом групп I–IV с той степенью строгости, конечно, с которой была построена и обоснована модель Пуанкаре в данном изложении.
Используя модель Пуанкаре, можно изучить свойства плоскости Лобачевского. На плоскости Лобачевского через каждую точку , не лежащую на прямой , проходит бесконечное множество прямых, не пересекающих прямую (рис. 15.2.15).
Все эти прямые заполняют два вертикальных угла, ограниченных прямыми и . Граничные прямые и , не пересекающие прямую , называются на плоскости Лобачевского параллельными прямой и проходящими через . Каждому направлению на прямой соответствует своя параллельная прямая, проходящая через .
Характерным свойством параллельных прямых на плоскости Лобачевского является то, что они неограниченно сближаются в направлении параллельности и неограниченно расходятся в противоположном направлении (рис. 15.2.16).
Те прямые на плоскости Лобачевского, которые и не пересекаются, и не параллельны, называются расходящимися . Характерное свойство расходящихся прямых – наличие у них единственного перпендикуляра.
В модели Пуанкаре параллельные прямые изображаются полуокружностями и лучами, касающимися на абсолюте (рис. 15.2.17, а).
На плоскости Лобачевского углы и длины связаны другими зависимостями, нежели на плоскости Евклида. Одно из характерных свойств плоскости выражается функцией Лобачевского 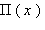
Из некоторой точки прямой проводится луч 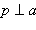
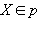
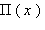
При возрастании от нуля до бесконечности функция 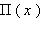
Существование таких зависимостей между длинами отрезков и углами означает, что на плоскости Лобачевского нет подобных фигур.
Например, на плоскости Лобачевского справедлив признак равенства треугольников: если углы одного треугольника соответственно равны углам другого треугольника, то такие треугольники равны. Сумма углов треугольника на плоскости Лобачевского меньше 180°. Разность между 180° и суммой углов треугольника называется избытком треугольника. Оказывается, что на плоскости Лобачевского площадь треугольника пропорциональна его избытку. Следовательно, на плоскости Лобачевского площади треугольников ограничены некоторой постоянной. Величины углов на плоскости Лобачевского в модели Пуанкаре равны величинам соответствующих углов на евклидовой плоскости. Поэтому все перечисленные свойства углов плоскости можно увидеть на модели Пуанкаре.
Для иллюстрации аксиомы о параллельности прямых рассмотрим следующую схему. Имея прямую и точку вне ее, соединяем с точкой , лежащей на , и отодвигаем точку в положение , , . и все дальше, и дальше на (иными словами, представляется последовательность точек , , , . или соответственно последовательность прямых , , , . ). Прямая при этом вращается вокруг и достигнет некоторого предельного положения, когда удалится в бесконечность, и эту предельную прямую и надо понимать как прямую, параллельную прямой , проходящую через .
При этом нет никаких изначальных соображений, в силу которых прямая должна приближаться к одному и тому же предельному положению при удалении в бесконечность как в одну, так и в другую сторону, что дает абстрактную возможность существования двух различных прямых, проходящих через , параллельных прямой . В этой связи постулат параллельных прямых в евклидовой геометрии – не что иное, как соглашение о том, что эти два предельных положения должны совпадать, и через точку должна проходить только одна прямая, параллельная прямой . На примере геометрии Лобачевского было показано, что допущение о несовпадении предельных прямых, а именно отрицание аксиомы о единственности прямой, проходящей через точку , не привело к противоречию, а наоборот, привело к построению новой неевклидовой геометрии. Однако наряду с геометрией Лобачевского существует еще один вид неевклидовой геометрии, которую полезно упомянуть.
- Реферат на тему «Геометрия Лобачевского»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Введение
- ТЕОРЕТИЧЕСКАЯ КОНЦЕПЦИЯ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО
- 1. Геометрия Лобачевского
- 2. Факты геометрии Лобачевского
- 3. Параллельные и сверхпараллельные прямые по Лобачевскому.
- 4. Пучки прямых и кривых на плоскости Лобачевского
- 5. Модели геометрии Лобачевского (модель Бельтрами-Клейна, модель Пуанкаре, модель в пространстве).
- ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО
- 1. Применение в повседневной жизни.
- 2. Примеры решения задач с помощью геометрии Лобачевского.
- Тесты
- Аксиома параллельности Лобачевского, основные следствия.
- 💡 Видео
Видео:1. Лобачевский и его наследие. Основные постулаты геометрии.Скачать

Реферат на тему «Геометрия Лобачевского»
Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ»
Геометрия Лобачевского. Факты геометрии Лобачевского. Параллельные и сверхпараллельные прямые по Лобачевскому. Пучки прямых и кривых плоскости Лобачевского. Модели геометрии Лобачевского (модель Бельтрами-Клейна, модель Пуанкаре, модель в пространстве).
студентка 4 курса
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Введение
Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий , геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия , за исключением аксиомы о параллельных , которая заменяется на аксиому о параллельных Лобачевского .
В конце прошлого века в работах Пуанкаре и Клейна была установлена прямая связь геометрии Лобачевского с теорией функций комплексной переменной и с теорией чисел (точнее, арифметикой неопределенных квадратичных форм). С тех пор аппарат геометрии Лобачевского стал неотъемлемым компонентом этих разделов математики. В последние 15 лет значение геометрии Лобачевского еще более возросло благодаря работам американского математика Тёрстона (лауреата Филдсовской медали 1983 г.), установившего ее связь с топологией трехмерных многообразий. Десятки работ ежегодно публикуются в этой области. Современные исследования все больше требуют делового владения геометрией Лобачевского.
Теория геометрии Лобачевского помогает взглянуть по-другому на окружающий нас мир, это интересный, необычный и прогрессивный раздел современной геометрии. Она дает материал для размышлений – в ней не все просто, не все ясно с первого взгляда, чтобы ее понять, нужно обладать фантазией и пространственным воображением.
Видео:Неевклидова геометрия Лобачевского — Валентина КириченкоСкачать

ТЕОРЕТИЧЕСКАЯ КОНЦЕПЦИЯ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО
Видео:Николай ЛобачевскийСкачать

1. Геометрия Лобачевского
Геометрия, как наука, впервые сформировалась в Древней Греции, когда геометрические закономерности и зависимости, найденные ранее опытным путем, были приведены в надлежащую систему и доказаны.
«Начала» — величайший памятник деятельности Евклида, в котором он собрал воедино всё то, что сделали его предшественники в области геометрии и «словесной алгебры». Но не только в этом его заслуга. Он также внёс много своего, нового, оригинального. Вплоть до XX века геометрию в школах преподавали по учебникам, в которые были включены евклидовы «Начала», переведённые и литературно обработанные.
Однако не всё написанное Евклидом удовлетворяло живших после него математиков. Он сделал попытку дать аксиоматическое изложение геометрии, т.е. сформулировать небольшое количество аксиом, из которых логически выводятся все теоремы геометрии. Список аксиом сразу же подвергся критике, некоторые из них оказались совсем не нужными, например, что «все прямые углы равны между собой».
Так называемый пятый постулат Евклида вызвал особые нарекания математиков. Именно эта аксиома, как показала историческое развитие науки, содержала в себе зародыш другой, неевклидовой геометрии.
Вот о чём говорится в пятом постулате: если две прямые a и b образуют при пересечении с третьей прямой односторонние внутренние углы α и β, сумма величин которых меньше двух прямых углов (т.е. меньше 180˚), то эти две прямые обязательно пересекаются, причём именно стой стороны от третьей прямой, по которую расположены углы α и β (составляющие вместе не менее 180˚).
Данное утверждение заметно сложнее остальных аксиом, поэтому пятый постулат часто заменяют равносильной аксиомой параллельности: через точку, лежащую вне данной прямой, можно провести не более одной прямой, лежащей с данной в одной плоскости и не пересекающей ее.
Попытки доказательства пятого постулата предпринимались в течение более чем двух тысячелетий сначала в Древней Греции, затем на средневековом Востоке, а позже в Западной Европе. Но неудачные попытки прямого доказательства направили ход мыслей ученных в иное русло. Пятый постулат решили заменить противоположным утверждением. Двери в новую геометрию приоткрыли такие ученые, как Джованни Саккери и Иоганн Ламберт, а их работу продолжили уже другие ученые, среди которых был выдающийся русский математик Николай Иванович Лобачевский.
Н. И. Лобачевский родился 20 ноября (1 декабря) 1792 года в Нижнем Новгороде. Окончил Казанскую гимназию в конце 1806 года, показав хорошие знания, особенно по математике и языкам — латинскому, немецкому, французскому. В проявившемся уже тогда его интересе к математике — большая заслуга преподавателя гимназии Г. И. Карташевского. В 15 лет поступил на физико-математический факультет Казанского университета. В это время там читал лекции по математике профессор И. Бартельс (1769-1836). Он обратил внимание на одаренного мальчика и начал заниматься с Лобачевским. В 19 лет Николай Иванович получил степень магистра, а в 23 года стал профессором. В течение 40 лет преподавал в Казанском университете, в том числе 19 лет руководил им в должности ректора; его активность и умелое руководство вывели университет в число передовых российских учебных заведений.
Еще до открытия неевклидовой геометрии Лобачевский написал в 1823г. учебное руководство, озаглавленное «Геометрия». В нем впервые со всей четкостью отражена так называемая теперь фузионистская точка зрения, согласно которой планиметрию не следует по евклидовой манере отрывать от стереометрии; наоборот, обе эти части геометрии нужно по возможности объединить, т.е. аналогичные начала планиметрии и стереометрии следует преподавать параллельно. Так рядом с кругом Лобачевский рассматривал шар и сферу; взаимное расположение прямых на плоскости он рассматривает совместно с взаимным расположением плоскостей в пространстве, почти одновременно трактует многоугольники и многогранники. Лишь в конце позапрошлого столетия итальянский математик Г. Веронезе также стал проводить в своих учебных руководствах по элементарной геометрии идею фузионизма.
Хотя Лобачевский занимался различными вопросами математики, мировую известность он получил как создатель новой геометрии. Лобачевский был с юношеских лет заинтересован аксиомой параллельных прямых. Сначала он пытался доказать пятый постулат, но постепенно пришел к выводу, что этого сделать нельзя, исходя из остальных аксиом. Тогда он заменил его на противоположное утверждение, которое сейчас называют аксиомой Лобачевского: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.
В разработанной Лобачевским новой геометрии многие утверждения звучат неожиданно. Вот некоторые из них:
1. Через точку А, не лежащую на прямой а, проходит бесконечное множество прямых, не пересекающих прямую а и лежащих с ней в одной плоскости.
2. Геометрическое место точек, равноудаленных от данной прямой, есть кривая линия.
3. Сумма углов треугольника – величина переменная. Она зависит от размера треугольника, но всегда меньше π.
4. Площадь треугольника вычисляется по формуле S = r 2 ( π – A – B – C ), где r – радиус кривизны пространства, а A , B , C – величины углов треугольника, выраженные в радианах
Остальные аксиомы Лобачевский оставил без изменения и на основе новой системы построил новую геометрию, отличную от евклидовой.
Можно считать, что неевклидова геометрия родилась в феврале 1826 года. Лобачевский выступил с докладом о своем открытии, но поддержки не нашёл. Математики его времени ещё не были подготовлены к мысли о возможности существования иной, неевклидовой геометрии. Учёный умер, так и не добившись признания своих идей. Впрочем, один человек понимал и поддерживал его работы.
Гениальный Гаусс, «король математиков» (судя по архиву, разобранному уже после смерти), ещё в 1815 г., за девять лет до сообщения Лобачевского, размышлял над аналогичными идеями. И тем не менее Гаусс, к мнению которого прислушивались все, не решился опубликовать свои работы. Однако Гаусс добился того, что Лобачевского избрали иностранным членом – корреспондентом Геттингенского учёного общества. Это единственная почесть, возданная Лобачевскому при жизни.
Видео:Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

2. Факты геометрии Лобачевского
Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому как это делается в геометрии Евклида. Основой служила теория параллельных линий, т. к. именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, общи обеим геометриям и образуют т. н. абсолютную геометрию, к которой относятся, напр., теоремы о равенстве треугольников. Вслед за теорией параллельных строились др. разделы, включая тригонометрию и начала аналитической и дифференциальной геометрий. Ниже перечислены неск. фактов геометрии Лобачевского, установленных самим Н. И. Лобачевским, которые отличают её от геометрии Евклида. [12]
1) В геометрии Лобачевского не существует подобных, но не равных треугольников; треугольники равны, если их углы равны. Поэтому существует абсолютная единица длины, т. е. отрезок, выделенный по своим свойствам, подобно тому как прямой угол выделен своими свойствами. Таким отрезком может служить, напр., сторона правильного треугольника с данной суммой углов.
2) Сумма углов всякого треугольника меньше ππ и может быть сколь угодно близкой к нулю. Это видно на модели Пуанкаре. Разность π−(α+β+γ)π−(α+β+γ), где α,β,γα,β,γ – углы треугольника, пропорциональна его площади.
3) Через точку, не лежащую на данной прямой, проходит бесконечно много прямых, не пересекающих прямую и находящихся с ней в одной плоскости; среди них есть две крайние, которые называются параллельными прямой в смысле Лобачевского. В моделях Клейна и Пуанкаре они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) общий конец.
4) Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают др. прямой.
5) Линия равных расстояний от прямой есть не прямая, а особая кривая, называемая эквидистантой или гиперциклом.
6) Предел бесконечно растущих окружностей есть не прямая, а особая кривая, называемая предельной окружностью или орициклом.
7) Предел сфер бесконечно увеличивающегося радиуса есть не плоскость, а особая поверхность – предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это послужило Лобачевскому основой для вывода формул тригонометрии.
8) Длина окружности не пропорциональна радиусу, а растёт быстрее, чем радиус.
9) Чем меньше область в пространстве или на плоскости Лобачевского, тем меньше метрические соотношения в этой области отличаются от соотношений евклидовой геометрии. Напр., чем меньше треугольник, тем меньше сумма его углов отличается от π, чем меньше окружность, тем меньше отношение её длины к радиусу отличается от 2π, и т. п. Уменьшение области формально равносильно увеличению единицы длины, поэтому при безграничном увеличении единицы длины формулы Л. г. переходят в формулы евклидовой геометрии. Евклидова геометрия есть в этом смысле «предельный» случай геометрии Лобачевского.
Видео:Воображаемый Лобачевский - 1/2Скачать

3. Параллельные и сверхпараллельные прямые по Лобачевскому.
В 19 веке Николай Иванович Лобачевский, а также немец Гаусс и венгр Больяи, предложили геометрию, в которой имеются минимум 2 прямые коллинеарные заданной. Эти прямые пересекаются между собой и приближаются к заданной прямой с двух различных направлений. Место их пересечения с заданной прямой находится в бесконечно удаленной точке. Непересекающиеся, но не параллельные прямые называются сверхпараллельными прямыми.
Теорема 1. Два перпендикуляра к одной прямой – сверхпараллельны.
Теорема 2. Две сверхпараллельные прямые имеют общий перпендикуляр и притом единственный, он является кратчайшим расстоянием между этими прямыми.
Теорема 3. Если две прямые при пересечении с третьей образуют равные соответственные углы или равные накрест лежащие углы, или внутренние односторонние углы, в сумме составляющие 2d, то эти прямые сверхпараллельны [12].
Видео:Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать

4. Пучки прямых и кривых на плоскости Лобачевского
Совокупность всех прямых плоскости Лобачевского, пересекающихся в общей точке О, называется пучком прямых первого рода. Точка О называется центром пучка.
Совокупность прямых плоскости Лобачевского, параллельных между собой в одном направлении, называется пучком прямых второго рода. Говорят также, что этот пучок имеет бесконечно удаленный центр.
Совокупность прямых плоскости Лобачевского, перпендикулярных одной прямой а, называется пучком третьего рода. Прямая а называется осью пучка. Говорят, также, что пучок прямых третьего рода имеет идеальный центр.
Множество всех прямых плоскости Лобачевского, проходящих через одну точку, будем называть пучком пересекающихся прямых. Множество всех расходящихся прямых, имеющих один и тот же общий перпендикуляр будем называть пучком расходящихся прямых. И множество всех прямых, параллельных между собой в одном и том же направлении, назовем пучком параллельных прямых. Точка пересечения прямых, принадлежащих пучку пересекающихся прямых, называется его центром. Общий перпендикуляр прямых, принадлежащих пучку расходящихся прямых, носит название его базы.
Теорема о серединных перпендикулярах к сторонам треугольника Серединные перпендикуляры сторон треугольника на плоскости Лобачевского принадлежат либо пучку пересекающихся, либо пучку расходящихся, либо пучку параллельных прямых, при этом существуют треугольники, серединные перпендикуляры которых принадлежат каждому из трех типов пучков. [12]
Свойства траекторий пучков
1) Траектория пучка симметрична относительно любой своей оси. Под хордой траектории пучка будем понимать отрезок, соединяющий его две точки.
2) Серединный перпендикуляр к хорде траектории является осью пучка.
3) Пусть АВ – хорда траектории пучка. Тогда прямая АВ образует равные углы с лучами траектории, проведенными в точках А и В.
Видео:7 класс, 28 урок, Аксиома параллельных прямыхСкачать

5. Модели геометрии Лобачевского (модель Бельтрами-Клейна, модель Пуанкаре, модель в пространстве).

Модель Пуанкаре плоскости Лобачевского
Анри Пуанкаре в 1882г. построил конформное отображение плоскости Лобачевского на открытую полуплоскость Евклида, тем самым, получив новую модель плоскости Лобачевского.

1) евклидовы полупрямые, перпендикулярные прямой l (рис.72) без точки пересечения с l .
2) евклидовы полуокружности, перпендикулярные абсолюту, т.е. с центром на прямой l.
На приведенном ниже рисунке 1 изображены четыре модели геометрии Лобачевского: модель Пуанкаре в верхней полуплоскости, модель Пуанкаре в круге (верхний ряд), модель Клейна (под моделью Пуанкаре в круге) и модель на верхней полусфере. Также в каждой из моделей нарисована кратчайшая сеть, соединяющая три заданных точки, и проведены некоторые дополнительные построения. Соответствие между объектами задано цветом. Так прямые в моделях Пуанкаре (верхний ряд) представляют собой окружности, перпендикулярные так называемому абсолюту – прямой или окружности, ограничивающей модель. В модели Клейна прямые – это прямолинейные хорды. Наконец, в модели верхней полусферы прямые представляют собой параллели, перпендикулярные абсолюту – граничному экватору. [12]
Видео:#177. ГЕОМЕТРИЯ ЛОБАЧЕВСКОГО (советский диафильм)Скачать

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ГЕОМЕТРИИ ЛОБАЧЕВСКОГО
Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

1. Применение в повседневной жизни.
Сам Лобачевский применял неевклидову геометрию для вычисления определенных интегралов при нахождении длины, площади или объема фигуры в своей геометрии. Но применение новых знаний не ограничилось математикой. Была установлена связь геометрии Лобачевского с физикой, а именно кинематикой – специальной (частной) теории относительности. Эта связь основана на том, что равенство,
выражающее закон распространения света x 2 + y 2 + z 2 = c 2 t 2 при делении на t 2 , даёт 
Интересно применение в игровой индустрии: игра «Жизнь» (модель зарождения жизни во «Вселенной») [ 9 ] или HyperRogue (гибрид паззла и рогалика на гиперболической плоскости). [ 3 ]
Применяется геометрия Лобачевского в живописи. В 2013 году в московском Музее современного искусства прошла выставка Маурица Корнелиса Эшера. Нидерландский художник-график известен благодаря своим работам, где он использует различные математические понятия, приемы и теории: пределы, ленты Мебиуса, геометрию Лобачевского. Заинтересовали работы-иллюзии и орнаменты. [ 2 ]

В 2015 году в Центральном зале центра дизайна ARTPLAY прошла еще одна не менее интересная выставка «Ван Гог. Ожившие полотна (Van Gogh Alive)». На его картинах отсутствует ровный фон, геометрия вангоговского пространства подчиняется законам, которые только предстояло открыть учёным 19-го столетия. Более того, во время просмотра посетители слушали классическую музыку. [ 1 ]
Использование геометрии Лобачевского в искусстве не ограничивается живописью. Творчество Фрэнка Гери тому доказательство. Он продемонстрировал возможности современных технологий проектирования. Его здания похожи друг на друга словно детали «конструктора из титана», но «мнет и гнет» он их каждый раз по-другому. В этом заключается уникальность дизайна построенных объектов. [ 11 ]

Спутниковые навигационные системы (GPS и ГЛОНАСС) состоят из двух частей: орбитальная группировка из 24-29 спутников, равномерно расположенных вокруг Земли, и управленческий сегмент на Земле, обеспечивающий синхронизацию времени на спутниках и использование ими единой системы координат. На спутниках установлены очень точные атомные часы, а в приемниках (GPS-навигаторах) обычные, кварцевые. В приемниках также есть информация о координатах всех спутников в любой момент времени. Спутники с маленькими интервалами передают сигнал, содержащий данные о времени начала передачи. Получив сигнал от не менее четырех спутников, приемник может скорректировать свои часы и вычислить расстояния до этих спутников по формуле ((время отправки сигнала спутником) – (время приема сигнала от спутника)) х (скорость света) = (расстояние до спутника). Вычисленные расстояния также корректируются по встроенным в приемник формулам. Далее, приемник находит координаты точки пересечения сфер с центрами в спутниках и радиусами, равными вычисленным расстояниям до них. Очевидно, это будут координаты приемника.
Формулы геометрии Лобачевского также используются в физике высоких энергий, а именно, в расчетах ускорителей заряженных частиц. Гиперболические пространства (т.е. пространства, в которых действуют законы гиперболической геометрии) встречаются и в самой природе. Приведем побольше примеров:
Геометрия Лобачевского проглядывается в структурах кораллов, в организации клеточных структур у растений, в архитектуре, у некоторых цветков и так далее. Кстати, если вы помните в прошлом выпуске мы рассказывали о шестиугольниках в природе, так вот, в гиперболической природе альтернативой являются семиугольники, которые также широко распространены
Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

2. Примеры решения задач с помощью геометрии Лобачевского.
Два спутника связи запустили на орбиту. Чтобы понять, пересекаются ли их зоны покрытия, необходимо доказать, что любые две прямые пересекаются.
В сферической геометрии окружность максимального радиуса называется «прямой» линией.

сфера(R;О),
две прямые на сфере
Доказать:
любые прямые пересекаются
Вторая «прямая» полностью лежит в одной из полусфер, потому что первая «прямая» делит сферу на две половины.
Поэтому её радиус (r) вторая «прямая» не является прямой => любые две «прямые» пересекаются на сфере, что и требовалось доказать.
Из-за загрязнения окружающей среды и появления озоновых дыр ученые прогнозировали на западном полушарии Земли потепление. Они описали его приблизительные размеры с использованием параллель и меридиан. Найти сумму углов предполагаемой зоны потепления, чтобы в дальнейшем 
Найти:
Сумму углов ΔABC, образованного двумя меридианами и параллелью.
AC перпендикулярна DF; AB перпендикулярна DF (как меридианы) => угол β и угол α = 90° =>
ΔABC = угол α + угол β + угол 1 = (90°·2) + 45°= 225°.

Дано:
сфера(R;О),
сфера разбита на 8 частей (равных) тремя ортогональными прямыми; каждая часть является сферическим треугольником.
Найти:
Сумму углов ABC.
Так как стороны треугольника ортогональны, углы треугольника по 90° => сумма углов ΔABC = 90°· 3 = 270°.
В модели геометрии Лобачевского в верхней полуплоскости найти радиус (в смысле геометрии Лобачевского) окружности, описанной около треугольника ABC, где A = (2; 6),
Верно ли, что около любого треугольника на плоскости Лобачевского
можно описать окружность? Верно ли это для сферической геометрии?
Нетрудно заметить, что любая окружность в модели геометрии Лобачевского в верхней полуплоскости является окружностью и в смысле евклидовой геометрии, но не наоборот. Например, если она пересекает Абсолют (т.е. ось абсцисс) под прямым углом, то она является прямой с точки зрения геометрии Лобачевского. Поэтому, для того, чтобы понять, что в геометрии Лобачевского не около любого треугольника можно описать окружность, достаточно взять какой-нибудь треугольник в верхней полуплоскости, описанная окружность которого выходит за ее пределы.
Легко проверить, что евклидова окружность, описанная около треугольника ABC, задается уравнением:
(x — 7) 2 + (y — 6) 2 = 25;
Очевидно, что она будет также и описанной окружностью с точки зрения геометрии Лобачевского, поскольку она целиком содержится в верхней полуплоскости. Найдем теперь ее центр. Пусть M = (7; 11) и N = (7; 1) — две диаметрально противоположные точки этой окружности, найдем середину O отрезка MN. Естественно выбирать именно этот диаметр рассматриваемой окружности, поскольку в метрики
Лобачевского совсем просто вычисляется расстояние между точками с одинаковой ординатой:
d (( x 0 ; y 1 ); ( x 1 ; y 2 )) =
Пусть O = (7; y), тогда для радиуса r нашей окружности имеют место равенства:
откуда 
Видео:24. Параллельные линии могут пересекаться. Такое возможно?Скачать

Тесты
В каждом задании выберите один из четырёх вариантов ответа.
1. Авторы неевклидовой геометрии
A. Лобачевский и Я. Больяи
B. Лобачевский, Больяи и Гаусс
C. Ламберт и Гаусс
D. Лобачевский и Ламберт
2. В геометрии Лобачевского сумма углов любого треугольника
A. меньше
B. больше
C. больше
D. больше 
3.В геометрии Лобачевского имеет место четвертый признак равенства треугольников:
A. если углы одного треугольника соответственно равны углам другого треугольника, то эти треугольники равны.
B. две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу ними другого треугольника
C. сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника
D. три стороны одного треугольника равны соответственно трем сторонам другого треугольника
4. Выберите свойства параллельных прямых на плоскости Лобачевского:
A. две параллельные прямые на плоскости Лобачевского имеют общий перпендикуляр
B. понятие параллельных прямых на плоскости Лобачевского транзитивно в данном направлении
C. понятие параллельных прямых на плоскости Лобачевского симметрично в данном направлении
D. расстояние между параллельными прямыми бесконечно убывает в направлении параллельности и неограниченно растет в противоположном направлении
5. Выберите свойства свехпараллельных прямых на плоскости Лобачевского:
A. две параллельные прямые на плоскости Лобачевского имеют общий перпендикуляр
B. понятие параллельных прямых на плоскости Лобачевского транзитивно в данном направлении
C. понятие параллельных прямых на плоскости Лобачевского симметрично в данном направлении
D. расстояние между параллельными прямыми бесконечно убывает в направлении параллельности и неограниченно растет в противоположном направлении
6. Если прямые 



A. прямые 

B. прямые 

C. прямые 

D. прямые 

7. На плоскости Лобачевского существует
A. три вида пучков прямых: пучок параллельных прямых в заданном направлении; пучок пересекающихся прямых; пучок сверхпараллельных прямых;
B. два вида пучков прямых: пучок параллельных и пучок пересекающихся прямых;
C. два вида пучков прямых: пучок параллельных и пучок сверхпараллельных прямых;
D. два вида пучков прямых: пучок пересекающихся и пучок сверхпараллельных прямых;
8. Плоскость Лобачевского реализуется в евклидовом пространстве
A. только в модели Пуанкаре на полуплоскости;
B. в модели Пуанкаре в круге, в модели Пуанкаре на полуплоскости; в модели Бельтрами –Клейна в круге; в модели на псевдосфере; в модели на одной полости двуполостного гиперболоида;
C. в модели Бельтрами –Клейна в круге; в модели на псевдосфере; в модели на одной полости двуполостного гиперболоида;
D. только в модели на псевдосфере;
9. В какой из геометрий верно утверждение: существует прямая линия, перпендикулярная к одной из двух параллельных прямых и параллельная к другой?
A. только в геометрии Евклида
B. только в абсолютной геометрии
C. только в геометрии Лобачевского
D. только в геометрии Римана
10. В какой из геометрий не существует понятия «подобие фигур»?
Видео:Параллельные прямые. 6 класс.Скачать

Аксиома параллельности Лобачевского, основные следствия.
LV1. (Аксиома параллельности Лобачевского). В любой плоскости существует прямая а0 и точка А0, не принадлежащая этой прямой, такие, что через эту точку проходит по крайней мере две прямые, не пересекающие а0.
Множество точек, прямых и плоскостей, удовлетворяющих аксиомам принадлежности, порядка, конгруэнтности, непрерывности и аксиоме параллельности Лобачевского будем называть трехмерным пространством Лобачевского и обозначать через Л3. Большинство геометрических свойств фигур будут рассматриваться нами на плоскости пространства Л3, т.е. на плоскости Лобачевского. Обратим внимание на то, что формальное логическое отрицание аксиомы V1, аксиомы параллельности евклидовой геометрии, имеет именно ту формулировку, которую мы привели в качестве аксиомы LV1. На плоскости существует, по крайней мере, одна точка и одна прямая, для которых не выполнено утверждение аксиомы параллельности евклидовой геометрии. Докажем теорему, из которой следует, что утверждение аксиомы параллельности Лобачевского справедливо для любой точки и любой прямой плоскости Лобачевского.
Теорема 13.1.Пусть а – произвольная прямая, А – точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует по крайней мере две прямые, проходящие через А и не пересекающие прямую а.
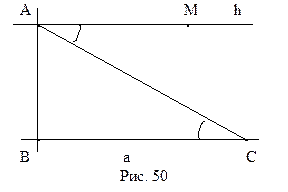
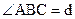
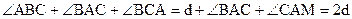
Следует заметить, что в дальнейшем мы будем пользоваться утверждением именно теоремы 13.1, по сути, заменяя им утверждение аксиомы параллельности Лобачевского. Кстати, во многих учебниках именно это утверждение принято в качестве аксиомы параллельности геометрии Лобачевского.
Из теоремы 13.1 легко получить следующее следствие.
Следствие 13.2. В плоскости Лобачевского через точку, не лежащую на данной прямой, проходит бесконечно много прямых, не пересекающих данную.
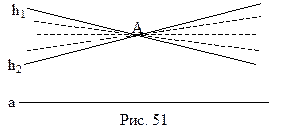
В главе 2 мы доказали ряд утверждений, эквивалентных аксиоме параллельности евклидовой геометрии. Их логические отрицания характеризуют свойства фигур на плоскости Лобачевского.
Во первых, на плоскости Лобачевского справедливо логическое отрицание пятого постулата Евклида. В параграфе 9 нами был сформулирован сам постулат и доказана теорема о его эквивалентности аксиоме параллельности евклидовой геометрии (см. теорему 9.1). Его же логическое отрицание имеет вид:
Утверждение 13.3.На плоскости Лобачевского существуют две непересекающиеся прямые, которые при пересечении с третьей прямой образуют внутренние односторонние углы, сумма которых меньше двух прямых углов.
В § 12 нами было сформулировано предложение Посидония: на плоскости существуют по крайней мере три коллинеарные точки, расположенные в одной полуплоскости от данной прямой и равноудаленные от нее. Также мы доказали теорему 12.6: предложение Посидония эквивалентно утверждению аксиомы параллельности евклидовой геометрии. Таким образом, на плоскости Лобачевского действует отрицание этого утверждения.
Утверждение 13.4. Множество точек, равноудаленных от прямой на плоскости Лобачевского и расположенных в одной полуплоскости относительно ее, в свою очередь не лежат на одной прямой.
На плоскости Лобачевского множество точек, равноудаленных от прямой и принадлежащей одной полуплоскости относительно этой прямой, образуют кривую линию, так называемую эквидистанту. Ее свойства будут рассмотрены нами позже.
Рассмотрим теперь предложение Лежандра: перпендикуляр, проведенный к стороне острого угла в любой точке этой стороны, пересекает вторую сторону угла. Доказанная нами теорема 11.6 (см. § 11) утверждает, что предложение Лежандра эквивалентно аксиоме параллельности евклидовой геометрии. Отсюда следует, на плоскости Лобачевского справедливо логическое отрицание этого предложения.
Утверждение 13.5. На стороне любого острого угла существует такая точка, что перпендикуляр к ней, восставленный в этой точке, не пересекает вторую сторону угла.
Отметим свойства треугольников и четырехугольников плоскости Лобачевского, которые непосредственно следуют из результатов параграфов 9 и 11. Прежде всего, теорема 11.1. утверждает, что предположение о существовании треугольника, сумма углов которого совпадает с суммой двух прямых углов, равносильно аксиоме параллельности евклидовой плоскости. Отсюда и из первой теоремы Лежандра (см. теорему 10.1, § 10) следует следующее утверждение
Утверждение 13.6. На плоскости Лобачевского сумма углов любого треугольника меньше 2d.
Отсюда непосредственно вытекает, что сумма углов любого выпуклого четырехугольника меньше 4d, а сумма углов любого выпуклого n – угольника меньше 2(n-1)d.
Так как на евклидовой плоскости углы, прилежащие к верхнему основанию четырехугольника Саккери равны прямым углам, что в соответствии с теоремой 12.3 (см. § 12) равносильно аксиоме параллельности евклидовой геометрии, то можно сделать следующий вывод.
Утверждение 13.7. Углы, прилегающие к верхнему основанию четырехугольника Саккери – острые.
Нам осталось рассмотреть еще два свойства треугольников на плоскости Лобачевского. Первое из них связано с предложением Валлиса: на плоскости существует хотя бы одна пара треугольников с соответственно равными углами, но не равными сторонами. В параграфе 11 мы доказали, что это предложение эквивалентно аксиоме параллельности евклидовой геометрии (см. теорему 11.5). Логическое отрицание этого утверждения приводит нас к следующему выводу: на плоскости Лобачевского не существует треугольников с равными углами, но не равными сторонами. Таким образом, справедливо следующее предложение.
Утверждение 13.8. (четвертый признак равенства треугольников на плоскости Лобачевского).Любые два треугольника на плоскости Лобачевского, имеющие соответственно равные углы, равны между собой.
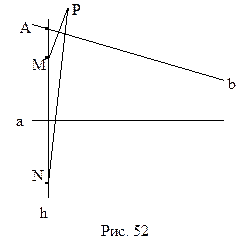
Утверждение 13.9. На плоскости Лобачевского существует треугольник, вокруг которого нельзя описать окружность.
Легко построить пример такого треугольника. Выберем некоторую прямую а и точку А, которая ей не принадлежит. Опустим из точки А перпендикуляр h на прямую а. В силу аксиомы параллельности Лобачевского существует прямая b, проходящая через А и не перпендикулярная h, которая не пересекает а (рис. 52). Как известно, если вокруг треугольника описана окружность, то ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника. Поэтому нам достаточно привести пример такого треугольника, серединные перпендикуляры которого не пересекаются. Выберем точку М на прямой h, так как показано на рисунке 52. Симметрично отобразим ее относительно прямых а и b, получим точки N и P. Так как прямая b не перпендикулярна h, то точка Р не принадлежит h. Поэтому точки M, N и P составляют вершины треугольника. Прямые а и b служат по построению его серединными перпендикулярами. Они же, как было сказано выше, не пересекаются. Треугольник MNP – искомый.
Легко построить пример треугольника плоскости Лобачевского, вокруг которого можно описать окружность. Для этого достаточно взять две пересекающиеся прямые, выбрать точку, которая им не принадлежит, и отразить ее относительно этих прямых. Проведите подробное построение самостоятельно.
Определение 14.1. Пусть даны две направленные прямые 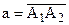
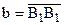
1. 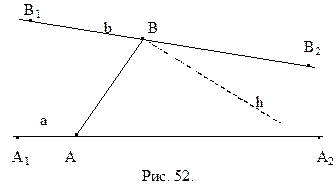
2. для произвольных точек А и В прямых а и b любой внутренний луч h угла АВB2 пересекает прямую а (рис. 52).
Обозначать параллельные прямые будем так же, как принято в школьном курсе геометрии: a || b. Заметим, что этому определению удовлетворяют параллельные прямые на евклидовой плоскости.
Теорема 14.3. Пусть на плоскости Лобачевского дана направленная прямая 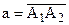
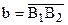
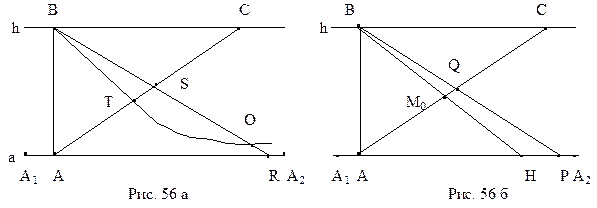
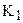
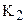
1. 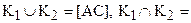
2. 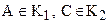
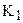
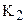
3. любая точка класса 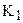
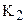
Первое условие очевидно, все точки отрезка принадлежат одному или другому классу, при этом сами классы, исходя из их определения, не имеют общих точек.
Второе условие также легко проверить. Очевидно, что 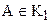
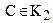
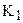
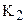
Докажем третье условие. Пусть существует такая точка S первого класса, отличная от А, и такая точка Т второго класса, что точка Т лежит между А и S (см. рис 56 а). Так как 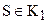
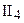
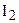
В соответствии с заключением теоремы 4.3 о дедекиндовом сечении на отрезке АС существует такая точка 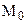
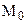
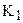
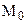
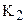
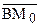
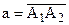
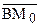
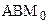

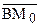
Легко проверить, что прямая 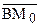

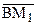
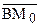

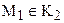
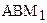

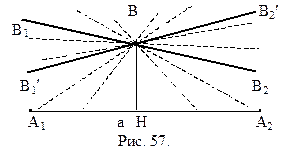
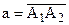
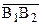
Теорема 14.4. Пусть направленная прямая 
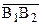
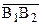

Из этой теоремы с очевидностью вытекает следующее следствие.
Следствие. Если существует общий перпендикуляр направленных прямых 
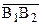

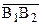
Введем понятие параллельности для ненаправленных прямых. Будем считать, что две ненаправленные прямые параллельны, если на них можно выбрать направления так, чтобы они удовлетворяли определению 14.1. Как известно, прямая имеет два направления. Поэтому, из теоремы 14.3 следует, что через точку В, не принадлежащей прямой а проходит две ненаправленные прямые, параллельные данной прямой. Очевидно, они симметричны относительно перпендикуляра, опущенного из точки В на прямую а. Эти две прямые и являются теми самыми пограничными прямыми, разделяющими пучок прямых, проходящих через точку В и пересекающих а, от пучка прямых, проходящих через В и не пересекающих прямую а (рис. 57).
Теорема 15.2. (Свойство симметричности параллельных прямых на плоскости Лобачевского).Пусть направленная прямая 
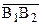
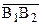

Свойство симметричности понятия параллельности прямых на плоскости Лобачевского позволяет нам не указывать порядок направленных параллельных прямых, т.е. не уточнять, какая прямая является первой, а какая второй. Очевидно, что свойство симметричности понятия параллельности прямых имеет место и на евклидовой плоскости. Оно непосредственно следует из определения параллельных прямых в евклидовой геометрии. В евклидовой геометрии выполняется также свойство транзитивности для параллельных прямых. Если прямая а параллельна прямой b, а прямая b параллельна прямой с. то прямые а и с также параллельны между собой. Аналогичное свойство справедливо и для направленных прямых на плоскости Лобачевского.
Теорема 15.3. (Свойство транзитивности параллельных прямых на плоскости Лобачевского).Пусть даны три различные направленные прямые 
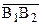
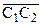
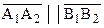
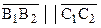
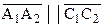
Рассмотрим направленную прямую 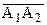
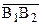
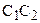
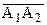
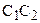
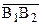
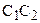
Теорема 15.4. Угол 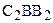
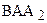
Теорема 15.5. Внешний угол вырожденного треугольника больше внутреннего угла, не смежного с ним.
Доказательство непосредственно следует из теоремы 15.4. Проведите его самостоятельно.
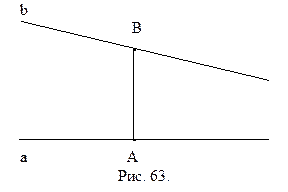
Определение 16.1. Острый угол, образованный прямыми АВ и b называется углом параллельности отрезка АВ.
Ясно, что каждому отрезку соответствует некоторый угол параллельности. Справедлива следующая теорема.
Теорема 16.2. Равным отрезкам соответствуют равные углы параллельности.
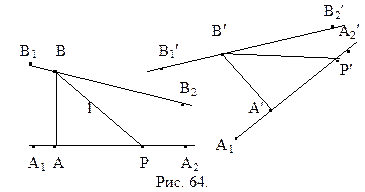
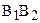
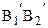
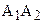
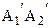
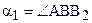
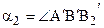
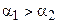
Отложим от луча ВА в полуплоскости ВАА2 угол a2, 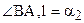
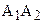
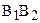
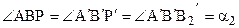
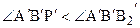
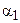
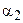
Рассмотрим теперь, как связаны между собой углы параллельности неравных отрезков.
Теорема 16.3. Пусть отрезок АВ больше отрезка А¢В¢, а углы 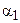
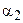
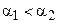
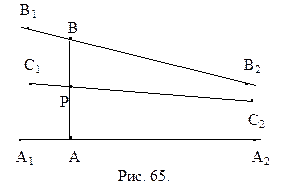
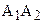
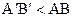
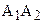
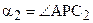
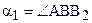
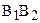
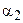
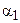
Легко доказать обратное утверждение.
Теорема 16.4.Пусть 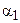
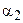
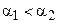
Доказательство.Предположим противное, 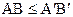
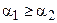
И так мы доказали, что каждому отрезку соответствует свой угол параллельности, причем большему отрезку соответствует меньший угол параллельности. Рассмотрим утверждение, в котором доказывается, что для любого острого угла существует отрезок, для которого этот угол является углом параллельности. Тем самым будет установлено взаимно однозначное соответствие между отрезками и острыми углами на плоскости Лобачевского.
Теорема 16.5. Для любого острого угла существует отрезок, для которого этот угол является углом параллельности.
Доказательство.Пусть дан острый угол АВС (рис. 66). 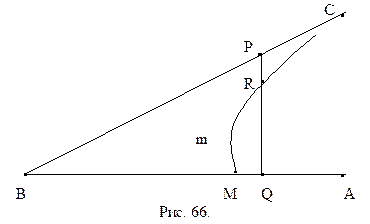
Разобьем точки отрезка ВМ на два класса. Классу 
4. 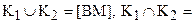
5. 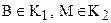
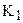
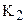
6. любая точка класса 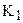
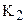
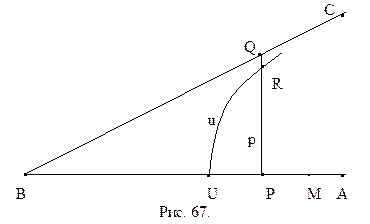
Проверим справедливость третьего условия теоремы 4.3. Предположим, что существуют такие точки 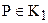
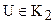
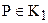
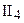
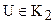
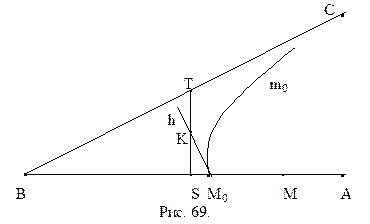
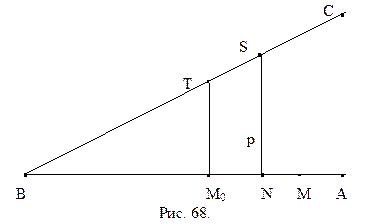
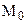
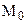
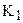
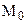
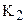
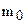
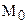
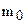
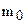
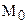
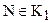
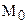
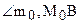
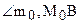
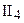
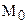
И так, мы установили, что каждому отрезку в геометрии Лобачевского можно поставить в соответствие острый угол – его угол параллельности. Будем считать, что нами введена мера углов и отрезков, отметим, что мера отрезков будет введена нами позже, в § . Ведем следующее определение.
Определение 16.6. Если под х понимается длина отрезка, а под j — величина угла, то зависимостьj = P(х), ставящая в соответствие длине отрезка величину его угла параллельности, называется функцией Лобачевского.
Ясно, что 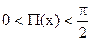
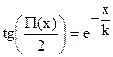
где k – некоторое положительное число. Оно имеет важное значение в геометрии пространства Лобачевского, и носит название его радиуса кривизны. Два пространства Лобачевского, имеющие один и тот же радиус кривизны, изометричны. Из приведенной формулы, как нетрудно видеть, также следует, что j = P(х) монотонно убывающая непрерывная функция, значения которой принадлежат интервалу 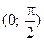
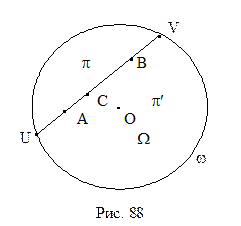
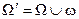
L‑плоскости имеет место аксиома параллельности Лобачевского: через L‑точку B, не лежащую на L‑прямой a проходят по крайней мере две L‑прямые b и c, не имеющие общих точек с L‑прямой a. На рисунке 94 приведена иллюстрация этого утверждения. Легко также понять, что из себя представляют параллельные направленные прямые L-плоскости. Рассмотрим рисунок 95. L-прямая b проходит через точку пересечения L-прямой a с абсолютом. Поэтому направленная L-прямая А1А2 параллельна направленной L-прямой В1А2. Действительно, эти прямые не пересекаются, и, если выбрать произвольные L-точки А и В, принадлежащие соответственно этим прямым, то любой внутренний луч h угла А2ВА пересекает прямую а. Таким образом, две L-прямые параллельны, если они имеют общую точку пересечения 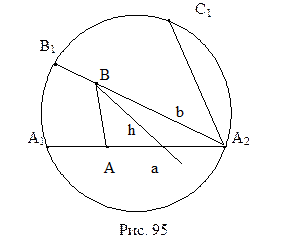
Таким образом, определенные выше основные понятия удовлетворяют требованиям аксиом I1-I3, II, III, IV групп аксиоматики Гильберта и аксиоме параллельности Лобачевского, следовательно являются моделью плоскости Лобачевского. Нами доказана содержательная непротиворечивость планиметрии Лобачевского. Сформулируем это утверждение как следующую теорему.
Теорема 1. Геометрия Лобачевского содержательно непротиворечива.
Мы построили модель плоскости Лобачевского, с построением же пространственной модели, аналогичной рассмотренной на плоскости, можно познакомиться в пособии [4].
Из теоремы 1 следует важнейший вывод. Аксиома параллельности не является следствием аксиом I – IV аксиоматики Гильберта. Так как пятый постулат Евклида равносилен аксиоме параллельности евклидовой геометрии, то этот постулат также не зависит от остальных аксиом Гильберта.
| | | следующая лекция ==> | |
| Тахеометрическая съемка | | | Параллельное проектирование и его свойства. |
Дата добавления: 2016-02-02 ; просмотров: 7112 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
💡 Видео
НЕЕВКЛИДОВАЯ ГЕОМЕТРИЯ. оказывается это так просто...Скачать

Неевклидова геометрия #shorts #nonEuclideangeometry #lobachevskyСкачать

НЕЕВКЛИДОВА ГЕОМЕТРИЯ - ЛЖЕНАУКА! ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ И КРИВОУГОЛЬНИКИ ЗА ДЕНЬГИ ПУТИНА? Катющик ТВСкачать

Свойства параллельных прямых - 7 класс геометрияСкачать

Математика это не ИсламСкачать

СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ. §15 геометрия 7 классСкачать












